martes, 9 de diciembre de 2014
Ponchar Cable UTP Categoria 6
http://www.slideshare.net/carjoshua/manual-ponchar-cable-red
Naranja-Blanco
Naranja
Verde-Blanco
Azul
Azul-Blanco
Verde
Cafe-Blanco
Cafe
lunes, 8 de diciembre de 2014
Albert Einstein
Complete Dictionary of Scientific Biography |
2008
|
Copyright
EINSTEIN, ALBERT
(b. Ulm, Germany, 14 March 1879;d. Princeton, New Jersey, 18 April 1955)
physics. For the original article on Einstein see DSB, vol. 4.
This essay extends and corrects the original entries by Martin J. Klein and Nandor L. Balazs, drawing on recent work in a variety of areas: experimental tests of general relativity and the role of the cosmological constant; new topics based on recently available information, such as the Einstein family business and its influence on young Einstein; his love affairs, first and second marriages, and other women in his life; black hole physics; and inadequate discussions of the nature of Einstein’s light quantum hypothesis; the reasons for his discontent with quantum mechanics; the origins of special relativity and the role of local time; the development of general relativity and the role of metric, affine connection, and Riemann tensor in the theory; his views on the significance of general relativity and the relation between physics and geometry; and his hopes for a unified field theory.
Einstein Family Business . The Einstein brothers’ Munich electrical engineering firm built and installed dynamos, power plants, and electric lighting systems, largely invented and patented by Albert’s uncle Jakob (1850– 1912), an engineer. The new, enlarged factory, started in 1885 with financial help from his mother Pauline’s (1858–1920) wealthy father, was managed by his father Hermann (1847–1902), a businessman. The dynamo division alone employed some fifty people. The firm was initially rather successful, and total employment at its height has been estimated at 150–200 (for the family business in Munich, see Hettler, 1996). But after an acrimonious dispute with its larger German rivals, the firm lost the lighting contract for the city of Munich in 1893.
The brothers decided to move to Northern Italy, where they had already installed several power plants, and in 1895 they built a large factory in Pavia. Their efforts to secure a contract to supply the city with electrical power failed due to various local intrigues, and they again had to liquidate their firm in 1896, losing almost everything in the process (for the Italian firm, see Winteler-Einstein, 1924). Uncle Jakob went to work for another firm but, despite Albert’s warnings, his father opened a small electrical firm in Milan. Albert helped out from time to time during school vacations, but was able to finish his education only with financial help from his mother’s wealthy family.
Prematurely aged by his financial troubles, Hermann died in 1902 deeply in debt to Rudolf Einstein (1843–1928), his cousin and brother-in-law. Young Albert had just started work at the Swiss Patent Office and was unable to support his mother or sister Maja (1881–1951). He had originally been destined to take over the family business and, as an adolescent, demonstrated considerable technical aptitude in electrotechnology, which later stood him in good stead at the Patent Office (1902–1909). But his father’s business failures and the attendant stress on the family contributed to an aversion to commercial activities for profit that ultimately led to his critique of capitalism and espousal of socialism (for Albert’s early development, see The Collected Papers, vol. 1, passim; and John Stachel, New Introduction” to Einstein, 2005). “I was also originally supposed to be a technical worker. But the thought of having to expend my inventive power on things, which would only make workaday life more complicated with the goal of dreary oppression by capital, was unbearable to me” (translation from Stachel, 2005, “New Introduction,” p. xxxiii; see Einstein, 1949, for his later condemnation of the profit system).
Einstein’s Love Affairs . The plaster saint image of Einstein, carefully cultivated by his executors, has been shaken by the disclosure of his many love affairs before, during, and after his two marriages. There is now a danger that the myth of the white-haired saint will be replaced by that of a devil incarnate (“father of the atom bomb,” “plagiarist,” “thief of his wife’s ideas”), but what is starting to emerge is something much more interesting than saint or devil: the rounded portrait of a human being (for a discussion of some common myths, see Brian, 2005).
While a student at the Aargau Kantonsschule (a Realschule, not a Gymnasium) in Aarau (1895–1896), Einstein boarded with the family of Jost (“Papa,” 1846–1929) Winteler, a teacher at the school and his wife Pauline (“Momma,” 1845–1906), with whom he developed close and lasting relationships. His sister later married Paul (1882–1952), one of the Winteler sons, and he had a brief love affair with their daughter Marie (1877–1957), which she later described as “innig [deep]” but “durchaus ideal [completely ideal].” It ended when he moved to Zurich in 1896 to attend the Zurich Poly (1896–1900), where he met Mileva Marić (1875–1948), the only other physics student to enter the program for teachers of mathematics and physics. The two began to study physics together and became intensely involved emotionally during their last years at the Poly. His letters to her from this period (see Einstein, 1992) are the major contemporary source of information on his scientific interests before his first published paper (1901). There is no evidence in his letters or in hers to support claims that she played more than a supporting role in his early research activities (for discussions of their relationship, see Stachel, 2002c; Stachel, 1996; and Martinez, 2005); she was the first of a series of “sounding boards” that he needed in order to help put the fruits of his research, carried out alone and with the aid of non-verbal symbolic systems, into a form that could be communicated to others (for further discussion, including an account of his mode of thought, see the “Introduction to the Centenary Edition” of Einstein, 2005).
After he graduated (she failed the final examinations twice due to poor grades in mathematics), they had a daughter out of wedlock, Lieserl (b. 1902), whose fate is unknown. But they lived apart until his job at the Swiss Patent Office (1902–1909) enabled their marriage in 1903. During these years Einstein did much of his research during working hours, and later stated, “The work on the final formulation of technical patents was a true blessing … and also provided important inspiration for physical ideas” (Einstein, 1956, p. 12). His first biographer reports: “He recognizes a definite connection between the knowledge acquired at the patent office and the theoretical results which, at that same time, emerged as examples of the acuteness of his thinking” (Moszkowski, 1921, p. 22).
In 1909 Einstein obtained his first academic post in theoretical physics at the University of Zurich, and his career slowly began to prosper, with successive posts in Prague and the Zurich Poly. He drifted away from Marić, later attributing his alienation to her taciturnity, jealousy, and depressive personality. By 1912 he was having an affair with Elsa Löwenthal (1876–1936), his cousin and childhood friend. She was a divorcee living in Berlin with her parents—her father Rudolf had been his father’s chief creditor. Albert’s move to Berlin in 1914 as a newly-elected member of Prussian Academy of Sciences precipitated a crisis in the marriage and Mileva returned to Zurich with their two sons, where she remained for the rest of her life.
After Albert’s divorce from Mileva and marriage to Elsa in 1919, he continued to have numerous affairs. In Berlin, the women included Betty Neumann, his secretary; Tony Mendel; and Margarete Lebach; after his move to Princeton in 1933 they included Margarita Konenkova, a Russian citizen living in the United States who has been accused of being a spy (see Pogrebin, 1998, for excerpts from his letters to Konenkova after her return to Russia in 1945; and Schneir, 1998, for contradictions in the spy story). His last close companion was Princeton librarian Johanna Fantova, an old friend from Europe (see Calaprice, 2005 for Fantova’s diary of her conversations with Einstein).
Einstein’s Light Quantum Hypothesis . In 1905 Einstein characterized only one of his papers as “very revolutionary,” the one that “deals with radiation and the energetic properties of light.” Klein comments: “Einstein leaped to the conclusion that the radiation … must consist of independent particle of energy” (p. 315), but a reading of the 1905 light quantum paper shows that he did not. He characterizes his demonstration that, in a certain limit, black body radiation behaves as if it were composed of energy quanta, as “a heuristic viewpoint”; and in 1909 warned against just this misunderstanding: “In fact, I am not at all of the opinion that light can be thought of as composed of quanta that are independent of each other and localized in relatively small spaces. This would indeed be the most convenient explanation of the Wien region of the radiation spectrum. But just the division of a light ray at the surface of a refracting medium completely forbids this outlook. A light ray divides itself, but a light quantum cannot divide without a change of frequency” (Einstein to H. A. Lorentz, 23 May 1909, Collected Papers, vol. 5, p. 193). It was only in 1915 that other considerations led him to attribute momentum to a light quantum (see p. 317), and only a decade later, after Bose’s work (see pp. 317–318) had shown that elementary particles need not be statistically independent, did he describe them as particles (see Stachel, 2000).
Speaking of Einstein’s first paper on mass-energy equivalence, Balazs writes: “[Einstein] observed that the exchange of radiation between bodies should involve an exchange of mass; light quanta have mass exactly as do ordinary molecules” (p. 323). But in his derivation of this result, Einstein speaks about a “light complex,” an entirely classical concept, rather than about a light quantum. In his early works, Einstein never mixed concepts from his quantum papers with those from his relativity papers. And when, after Bose’s work, he did attribute corpuscular properties to light quanta, he distinguished clearly between photons (a word he did not use), zero rest mass bosons (another word introduced later) whose number need not be conserved; and massive bosons, whose number must be conserved. His prediction of a condensed state for massive bosons (see Einstein, 1925), now called a Bose-Einstein condensate, offered the first theoretical explanation of a transition between two phases of a system. The prediction was spectacularly confirmed some seventy years later, winning its discoverers the 2001 Nobel prize in physics.
Discontent [Unbehagen] with Quantum Mechanics . Speaking of Einstein’s “Discontent with Quantum Mechanics,” Klein cites (p. 318) its basically statistical nature and presumed incompleteness as the reasons. Actually, Einstein believed that, if one adopted the statistical ensemble interpretation of quantum mechanics (which he referred to as the Born interpretation, but had actually adumbrated; see Stachel, 1986, Sections 5 and 7), there was no problem with the theory. For him, the problem came when the theory was applied to an individual system: it was here that the issue arose of completeness of the quantum mechanical description. A careful reading of his comments on this topic (see Stachel, 1986) shows that the issue of non-separability was the most fundamental cause of his “Unbehagen.” As Wolfgang Pauli explained: “Einstein does not consider the concept of ‘determinism’ to be as fundamental as it is frequently held to be. … he disputes that he uses as a criterion for the admissibility of a theory the question ‘Is it rigorously deterministic?’” (Pauli to Max Born, 31 March 1954, quoted from Stachel, 1991, p. 411). Once they interact, two quantum systems remain entangled, no matter how far apart in time and space they may have traveled. To Einstein, this seemed to contradict his expectation, based on the role of space-time in his relativity theories, that two systems, sufficiently separated in space-time, should not exert any physical influence on each other.
Does it make sense to say that two parts A and B of a system do exist independently of each other if they are (in ordinary language) located in different parts of space at a certain time, if there are no considerable interactions between those parts … at the considered time? … I mean by “independent of each other” that an action on A has no immediate influence on the part B. In this sense I express a principle a) independent existence of the spatially separated. This has to be considered with the other thesis b) the ψ-function is the complete description of the individual physical situation. My thesis is that a) and b) cannot be true together .… The majority of quantum theorists discard a) tacitly to be able to conserve b). I, however, have strong confidence in a), so I feel compelled to relinquish b). (Einstein to Leon Cooper, 31 October 1949, quoted from Stachel, 1986, p. 375)Since then the formulation of Bell’s inequality and its experimental testing by Clauser, Horne, and Shimony, and by Aspect, have convinced most physicists that quantum entanglement is not the result of an incompleteness due to neglected statistical correlations, as Einstein suggested. Whatever the ultimate fate of contemporary quantum mechanics, entanglement seems destined to remain a fundamental feature of any future physical theory (for a review of this topic, with references to the original literature, see Shimony, 2006).
Origin of Special Relativity . Balazs points out: “By [Einstein's] own testimony the failure of the ether-drift experiments did not play a determinative role in his thinking but merely provided additional evidence in favor of his belief that inasmuch as the phenomena of electrodynamics were ‘relativistic,’ the theory would have to be reconstructed accordingly” (p. 320). In fact, the phenomena of the optics of moving bodies also played a major role in the development of his ideas. In 1952 he wrote: “My direct path to the special theory of relativity was mainly determined by the conviction that the electromotive force induced in a conductor moving in a magnetic field is nothing other than an electric field. But the result of Fizeau’s experiment and the phenomenon of aberration also guided me” (quoted from Stachel, 1989, p. 262).
As Balazs explains (p. 320), the conductor-magnet example suggested to Einstein that the relativity principle must be extended from mechanics to electromagnetic theory. He then attempted to reconcile the relativity principle with well-known optical phenomena, in particular the
constancy of the velocity of light. Two main alternatives presented themselves: (1) The velocity of light is independent of that of its source, constant relative to the ether; or (2) The velocity of light is constant relative to its source (ballistic theory of light—light behaves like a bullet).
Lorentz’s version of Maxwell’s theory, based on the first alternative, was able to explain the result of Fizeau’s experiment and the phenomenon of aberration, but did not seem to be compatible with the relativity principle— the ether frame of reference is special. So Einstein explored the second alternative, where the situation was just the reverse: The relativity principle presented no problem if one assumed that a moving medium dragged the ether along within it. But Fizeau’s experiment on the velocity of light in moving water, interpreted within the framework of an ether theory, seemed to preclude the idea that ether was totally dragged along by matter. Rather, it confirmed Fresnel’s formula, which had been developed to account for aberration and predicted a partial dragging of the ether (see Stachel, 2005a).
Attempts to explain Fizeau’s experiment using the second alternative led to more and more complications, so Einstein returned to the first, but with a crucial difference: he dropped the ether. He realized that the relativity principle then requires the velocity of light to be a universal constant, the same in all inertial frames of reference. But how is this possible? He pondered this question for several years. Finally in 1905 came the insight that removed the puzzle. It is possible if one gives up the Galileian law of addition of relative velocities! A reanalysis of the concept of time showed that the proof of this law depended on the existence of an absolute time, which implies that one can always say whether two events are simultaneous, however far apart. But careful analysis of the concept of simultaneity showed that one must define when two events occurring at some distance from each other are simultaneous. He showed that one could adopt definition that made the velocity of light the same in all inertial frames—but this definition gives a different answer in each inertial frame and results in a new law for addition of relative velocities.
Einstein’s new definition of frame-dependent time is closely related to Lorentz’s concept of local time, as Balazs points out “Although Lorentz appears to have viewed local time as a mathematical artifice, it represented in embryo a concept of time that Einstein would later justify adopting for the whole of physics” (p. 321). In 1900 Poincaré had given a physical interpretation of the local time within the ether-theoretical framework: It is the time that clocks in a moving frame of reference would read (compared with clocks at rest in the ether, which read the true, absolute time) if they were synchronized using light signals, but without correcting for the effects of motion through the ether on the propagation of light. Einstein may well have been familiar with Poincaré’s work, but his crucial idea was to drop all reference to the ether and accept the local time of each inertial frame as just as good as that of any other.
Development of General Relativity . Einstein divided his work on general relativity into three key steps (for the first two steps, see Stachel, 2002b; for the third step, see Janssen et al., 2007, vol. 2.).
The first step, in 1907, was his “basic idea for the general theory of relativity” (Stachel, 2002b, p. 261). He was referring to his formulation of the equivalence principle—the inability to uniquely separate gravitation and inertia. Balazs states: “Einstein published two remarkable memoirs in 1912 which were efforts to construct a complete theory of gravitation incorporating the equivalence principle” (p. 326). Actually, they were an attempt to construct equations only for a static field, as well as the equations of motion of a test particle in such a field. His recognition that the latter equations describe the geodesics of a non-flat space-time was a major clue that led to the second step, in 1912: his “recognition of the non-Euclidean nature of the metric and of its physical determination by gravitation” (Stachel, 2002b, p. 261). He was referring to the adoption of the metric tensor as the representation of the gravitational potentials.
The third step came with his “1915 field equations of gravitation. Explanation of the perihelion motion of Mercury” (Stachel 2002b, p. 261). Einstein was referring to the final form of the field equations, which he announced on 25 November 1915. This corrects the erroneous date of 25 March given in the table on p. 324 and on p. 327. The correct date, when combined with Balazs’ statement: “[O]n 20 November, David Hilbert, in Göttingen, independently found the same field equations” (p. 327). might suggest that Hilbert actually had priority, a claim that is still maintained by some scholars in the face of new evidence to the contrary (for a review of Hilbert’s role in the development of general relativity, see Renn and Stachel, 2007).
Role of the Affine Connection . A fourth key step may be added: Recognition of the affine connection and parallel displacement as the correct mathematical representation of the inerto-gravitational field (for a discussion of the role of the affine connection in the development of gravitation theory, see Stachel, 2007). This step was first taken by Tullio Levi-Civita in 1917, but Einstein came to recognize its crucial importance:
It is the essential achievement of the general theory of relativity that it freed physics from the necessity of introducing the “inertial system” (or inertial systems). (The Meaning of Relativity, p. 139)The mathematical formulation of the equivalence principle is that “the displacement field,” also called the affine connection, represents a single inertio-gravitational field.
The development … of the mathematical theories essential for the setting up of general relativity had the result that at first the Riemannian metric was considered the fundamental concept on which the general theory of relativity and thus the avoidance of the inertial system were based. Later, however, Levi-Civita rightly pointed out that the element of the theory that makes it possible to avoid the inertial system is rather the infinitesimal [parallel] displacement field Γlik.. The metric or the symmetric tensor field gik which defines it is only indirectly connected with the avoidance of the inertial system in so far as it determines a displacement field. (The Meaning of Relativity, p. 141)
In all previous physical theories, including the special theory, the space-time structures, metric and connection, had been fixed, background fields, determining the kinematics of space-time: the stage, on which the drama of matter and dynamical fields takes place. With the dynamization of these space-time structures, the stage now became part of the play; moreover a new kind of physics was born, now called background-independent to contrast it with all theories based on fixed background space-time.
Balazs writes: “Gravitation is a universal manifestation because it is a property of space-time, and hence everything that is in space-time (which is, literally, everything) must experience it” (p. 331). But Einstein opposed such a “container” or absolute concept of space-time and forcefully advocated a relational approach to space-time (see, for example, Einstein, 1954), preferring to say that space-time is a property of the gravitational field:
[A]ccording to the special theory of relativity, space (space-time) has an existence independent of matter or field. In order to be able to describe at all that which fills up space …, space-time or the inertial system with its metrical properties must be thought of at once as existing, for otherwise the description of “that which fills up space” would have no meaning. On the basis of the general theory of relativity, on the other hand, space as opposed to “what fills space” … has no separate existence. … If we imagine the gravitational field, i.e., the functions gik to be removed, there does not remain a space of the type (1) [Minkowski space-time], but absolutely nothing, and also no “topological space”. … There is no such thing as an empty space, i.e., a space without field. Space-time does not claim existence on its own, but only as a structural quality of the field. (Einstein, 1952, p. 155).Balazs writes: “In this way Einstein showed that gravitational fields influence the motion of clocks” (p. 325). Presumably, Balazs meant the rate of clocks, but even that statement would be inaccurate. General relativity is built precisely on the assumption that (ideal) clocks and measuring rods are not affected by the presence of an inertio-gravitational field. However, the rates of two clocks at different places in a gravitational field cannot be directly compared. (If the two clocks are brought to the same place for direct comparison, according to general relativity they will always agree!) Some signal must pass between them. It is the difference between the frequency with which a signal is emitted by one clock and the frequency with which the signal is detected at the position of the other clock that is responsible for gravitational effects on time measurements, such as the gravitational red shift.
Balazs writes “In particular [Einstein] assumed that … the history of a body will be a geodesic … the curve in space-time for which ∫ds is a minimum, δ∫ ds= 0” (p. 227). While this integral is always an extremal of the space-time interval for geodesic curves, for time-like paths it is a maximum. This is the basis of the twin paradox: The stay-at-home, non-accelerating twin will be much older than his adventurous, accelerating sibling when the two meet again.
Balazs writes “Θμν; contains the material sources of the field … In any given physical situation, the Θ μν; may be assumed known” (p. 227). In fact, the expression for Θμν;, the stress-energy-momentum tensor (later in the article symbolized by Tμν;), almost always contains the metric tensor, so the gravitational field equations cannot be solved separately. Rather, one must solve the coupled sets of equations for the source fields and for the metric field.
Curvature Tensors and Field Equations . Balazs writes “[T]he gravitational field can be characterized by Riemann’s curvature tensor Gµν .… [Einstein] wrote the gravitational field equations as Gµν = K(Tµν - 1/2 gµνTT), where T is the scalar of the material energy tensor Tµν and K is a gravitational constant. … The curvature of space-time at a point is determined by the amount of matter and electromagnetic field and their motion at that point” (p. 328). There are several errors here. First, Balazs’ Gµν is the Ricci tensor, not the Riemann curvature tensor. The Riemann tensor is a four-index tensor Rκµλν, the trace of which is equal to the Ricci tensor: Rκµκν,= Gµν, in Balazs’ notation. The Ricci tensor is more commonly denoted by Rµν, whereas Gµν is used to denote the Einstein tensor Rµν - 1/2 gµν R, where R is the trace of the Ricci tensor. The gravitational field equations are now more commonly written in the form: Rµν - 1/2 gµνR = KTµν, which is equivalent to Einstein’s original form.
Second, according to Einstein, it is the affine connection that defines the inertio-gravitational field, not the Riemann tensor:
What characterizes the existence of a gravitational field from the empirical standpoint is the non-vanishing of the Γlik [components of the affine connection], not the non-vanishing of the Riklm [the components of the Riemann tensor]. If one does not think in such intuitive ways, one cannot comprehend why something like curvature should have anything at all to do with gravitation. (Einstein to Max von Laue 1950; English translation from Stachel, 1989, p. 326)The affine connection is not a tensor between systems of such particles. The Riemann tensor is built from its components and their first derivatives. The affine connection enters the geodesic equation—it would actually be better to say the equation for autoparallel or straightest lines—describing the motion of freely falling sructureless particles, while the Riemann tensor enters the equation of geodesic deviation, which characterizes the tidal gravitational forces between such particles.
A metric affine connection, as in general relativity, is built from the components of the metric and their first derivatives. In this case, the autoparallel lines are also metric geodesics. It follows that a metric Riemann tensor depends on the metric tensor and its first and second derivatives. In spite of Einstein’s comments cited above, general relativity is still often presented entirely in terms of the metric tensor and its derivatives, without proper emphasis on the role of the connection.
The third error is that the curvature at a point of space-time is not “determined by the amount of matter and electromagnetic field and their motion at that point.” The Riemann tensor determined by a metric has twenty independent components at each point, and only the ten components of the Ricci tensor are so determined. It is the additional ten components that enable the propagation of gravitational waves, even in “empty” regions of space-time, that is, regions in which the Ricci tensor vanishes.
Tests of the General Theory . The theory has survived much more precise observations of the three classic predictions: the anomalous precession of Mercury’s orbit, the gravitational red shift, and the apparent bending of light beams in strong gravitational fields. Indeed, the relativistic effects are now so well confirmed that they are routinely used in many new applications (for surveys, see Damour, 2006 and Will, 2005).
The gravitational bending effect is the basis of the phenomenon known as gravitational lensing, originally predicted by Einstein around 1912, but not published by him until 1936 (for Einstein’s role, see Renn, Sauer, and Stachel, 1997). It is now a major tool in observational cosmology, particularly the study of the effects of “dark matter” in galaxies and clusters on light propagation (for gravitational lensing, see Schneider, Ehlers, and Falco, 1992). On a more everyday level, the ubiquitous Global Positioning System (GPS) could not operate without taking into account both special and general relativistic effects (see Ashby, 2005).
The major outstanding project is the direct detection of gravitational waves. Indirect confirmation of the emission of quadrupole gravitational radiation by the binary pulsar PSR 1913+16 through measurement of the resulting modification of the presumed back reaction on their orbits has been extremely successful, winning its observers the Nobel Prize for Physics in 1993 (see Will, 2005). But instruments designed to detect the radiation itself, notably the Laser Interferometer Gravitational-Wave Observatory (LIGO), did not attain sufficient sensitivity to “see” the extremely weak radiation predicted from astrophysical sources (see Saulson, 2005), or the even weaker background cosmological gravitational radiation predicted by some models of the early universe.
The Cosmological Constant . As Balazs points out, Einstein originally introduced the cosmological constant Λ in 1916 order to implement what he called Mach’s principle: On a cosmological scale, the metric tensor field should be completely determined by matter. Einstein took it for granted that, on the average, the universe was static, so he developed such a static cosmological model, for which he needed Λ. When Alexander Friedmann first showed that there are non-static cosmological models with and without the cosmological constant, Einstein thought he had found an error in Friedmann’s work. He quickly withdrew that claim, but regarded the expanding universe solutions as mere mathematical curiosities until the observations of Hubble around 1930 showed their importance for cosmology. By this time Einstein had abandoned Mach’s principle in favor of the reverse, unified field viewpoint: The properties of matter should be completely determined by solutions to some set of unified field equations. Thus, the cosmological constant was no longer needed for its original purpose and there were expanding cosmological models without it, so Einstein abandoned the concept. Others, such as Eddington, kept Λ for other reasons, and it maintained a precarious foothold in cosmological speculations.
In the latter third of the twentieth century, the situation in cosmology began to change dramatically. Theoretical cosmology became more and more closely associated with elementary particle theory, and observational cosmology began to accumulate more and more data limiting the possibilities for and influencing the construction of cosmological models. The cosmological constant has had a dramatic rebirth with the accumulating observation evidence that, rather than slowing down as current theories had predicted, the expansion of the universe is actually accelerating with cosmic time. By an appropriate choice of sign and value for Λ, cosmological models with this property are easily constructed. The problem is to give a physical explanation for such a choice of Λ. One favored explanation as of 2007 is that the Λ-term in the field equations is actually the stress-energy-momentum tensor for “dark energy,” a hitherto unobserved component pervading the entire universe. If this explanation stands the test of time, it may also turn out that the “cosmological constant” is not constant, but varies with cosmological time! (For a review of developments in cosmology, see Padmanabhan, 2005.)
Black Hole Physics . Since the original edition of the DSB, an entire industry has grown up within theoretical physics and observational astronomy known as “black hole physics” (for reviews, see Carter, 2006, and Price, 2005). It is based theoretically on the existence of two solutions to the homogeneous Einstein field equations: the static, spherically symmetric Schwarzschild solution, dating from 1916, and the stationary, axially symmetric Kerr solution, dating from 1963. (For reviews of these and other exact solutions to the Einstein equations, see Bičak, 2000.) Astrophysics predicts that sufficiently massive astrophysical objects ultimately undergo gravitational collapse as gravitation overwhelms the pressures and stresses that keep them from collapsing. If they are massive enough, this process will not be halted by the formation of a neutron star, but will continue until the system passes through an event horizon and forms a black hole, which ultimately ends in a singularity, signaling the breakdown of classical general relativity. This is the upshot of the famous Penrose-Hawking singularity theorems. The external gravitational field outside the horizon must ultimately take the form of either the Schwarzschild field if the system has no net angular momentum, or the Kerr solution if it does. This result was picturesquely stated as “black holes have no hair” by John Wheeler, who coined the term “black hole.” Classically, except for their gravitational fields, such black holes have no influence on their exterior, but Stephen Hawking showed that a semi-classical treatment of quantum-mechanical effects predicts the formation of a radiation field outside the black hole that behaves like black-body radiation at a temperature dependent on the mass of the black hole. Much theoretical work is being done in the early 2000s in the attempt to find an exact quantum-gravitational treatment of black holes, and much observational work on the search for black holes in the cosmos.
Relation Between Geometry and Physics . Balazs asserts: “Minkowski recast the special theory of relativity in a form which had a decisive influence in the geometrization of physics. … This very strong geometrical point of view … led to Einstein’s belief that all laws of nature should be geometrical propositions concerning space-time” (p. 323). Einstein’s supposed “views on the geometrization of physics” are repeated: “He felt that not only the gravitational but also electromagnetic effects should be manifestations of the geometry of space-time” (p. 325). Although many people continue to hold this view of Einstein’s accomplishment and attribute it to him, Einstein explicitly rejected it. In 1928 he wrote: “I cannot agree that the assertion relativity reduces physics to geometry has a clear meaning. One can more correctly say that it follows from the theory of relativity that (metric) geometry has lost its independent existence with respect to the laws usually classified as physical. … That this metric tensor is designated as ‘geometrical’ is simply connected with the fact that the formal structures concerned first appeared in the science called ‘geometry.’ But this is not at all sufficient to justify applying the name ‘geometry’ to every science in which this formal structure plays a role, even when for purposes of visualization [Veranschaulichung] representations are used, to which geometry has habituated us. …” He explicitly rejected the idea that the search for a unified field theory was an attempt to geometrize the electromagnetic field: “The essential thing in Weyl’s and Eddington’s theoretical representations of the electromagnetic field does not lie in their having embedded the field in geometry, but that they have shown a possible way to represent gravitation and electromagnetism from a unified point of view” (Einstein, 1928; translated from the German manuscript, The Einstein Archives Online, Call Nr. [1-68.00]). Peter Bergmann has suggested that “physicalization of geometry” would be a more appropriate phrase (see Bergmann, 1979; the phrase had been used in Zubirini, 1934).
Balazs asserts: “[T]he geometrization of gravitation led eventually to the general theory of relativity; the additional geometrization of the electromagnetic fields of force led to the invention of the unified field theories.” Apart from the use of geometrization language, criticized above, the statement may be misleading. The most successful “geometrization of the electromagnetic fields of force” has been achieved as part of the modern gauge theory of Yang-Mills fields. This has served to unify the electromagnetic and weak nuclear forces, and to a lesser extent, in the theory of quantum chromodynamics, the strong nuclear forces, in the so-called Standard Model. The formulation and quantization of these theories is based on the mathematics of gauge natural fiber bundles, while the standard formulation of general relativity only requires natural bundles. While classical gravitation theory also can be formulated as a gauge natural bundle theory, as of 2007 no successful quantization based on this approach has been accomplished—let alone a unified quantum theory including gravitation (for natural and/or gauge natural theories see Fatibene and Francaviglia, 2003).
Einstein and Unified Field Theory . Balazs states: “Between 1907 and 1911 … [Einstein] came to understand that the solution to the dualism [of fields and particles] problem was to write physics in terms of continuous field quantities and nonlinear partial differential equations that would yield singularity-free particle solutions” (pp. 325–326). Similarly, Klein states “[Einstein] never lost his hope that a field theory of the right kind might eventually reach this goal” (pp. 318–319). Actually, as early as 1916, Einstein was presenting arguments suggesting that the continuum was too rich a structure for the treatment of quantum phenomena (for the evolution of his ideas between 1902 and 1954, see Stachel, 1993). While he continued to work on the topic, his hopes for a satisfactory unified field theory grew weaker in his later years, as Balazs himself suggests: “In 1953 Einstein said to the author that … it is doubtful that a unified field theory of the type he was seeking could exist” (p. 330).
Here is Einstein’s last published comment on the subject, written shortly before he died:
One can give good reasons why reality cannot at all be represented by a continuous field. From the quantum phenomena it appears to follow with certainty that a finite system of finite energy can be completely described by a finite set of numbers (quantum numbers). This does not seem to be in accordance with a continuum theory, and must lead to an attempt to find a purely algebraic theory for the description of reality. But nobody knows how to obtain the basis of such a theory. (“Appendix II” to The Meaning of Relativity, 5th ed. Princeton, 1955, p. 166)Much recent work on quantum gravity has been based on attempts to set up just such a “purely algebraic theory.” For reviews of some attempts, see Gambini and Pullin, 2005; Dowker, 2005; and Ambjorn, Jurkiewicz, and Loll, 2006.
SUPPLEMENTARY BIBLIOGRAPHY
For the Einstein Archives in the Hebrew University of Jerusalem, consult http://www.albert-einstein.org For the Einstein Papers Project, consult http://www.einstein.caltech.edu For updated reviews of most topics in general relativity, consult http://relativity.livingreviews.org.WORKS BY EINSTEIN
“Quantentheorie des einatomigen idealen Gases. Zweite Abhandlung.” Preussische Akademie der Wissenschaften(Berlin) Physikalisch-mathematische Klasse. Sitzunsberichte (1925): 3–14.“A propos de la déduction relativiste de M. Emile Meyerson.” Revue Philosophique 105 (1928): 161–166.
“Lens-Like Action of a Star by the Deviation of Light in a Gravitational Field.” Science84 (1936): 506–507.
“Why Socialism.” Monthly Review (May 1949). Reprinted in Ideas and Opinions. New York: Crown Publishers, 1954, 151–158.
“Relativity and the Problem of Space.” In Relativity: The Special and the General Theory. 15th ed. New York: Crown, 1952. Reprinted in Ideas and Opinions. New York: Crown Publishers, 1954.
“Foreword.” In Concepts of Space, by Max Jammer . Cambridge, MA: Harvard University Press, 1954.
“Autobiographische Skizze.” In Helle Zeit- Dunkle Zeit In Memoriam Albert Einstein, edited by Carl Seelig. Zürich: Europa, 1956.
The Collected Papers of Albert Einstein. Translated by Anna Beck. Princeton, NJ: Princeton University Press, 1987–2004. Vol. 1: The Early Years, 1879–1902. Vol. 2: The Swiss Years: Writings, 1900–1909. Vol. 3: The Swiss Years: Writings, 1909–1911. Vol. 4: The Swiss Years: Writings, 1912–1914. Vol. 5: The Swiss Years: Correspondence, 1902–1914. Vol. 6: The Berlin Years: Writings, 1914–1917. Vol. 7: The Berlin Years: Writings, 1918–1921. Vol. 8: The Berlin Years: Correspondence, 1914–1918. Vol. 9: The Berlin Years: Correspondence, January 1919–April 1920. Vol. 10: The Berlin Years: Correspondence, May-December 1920, and Supplementary Correspondence, 1909–1920. Cited as Collected Papers. These volumes are making available a wealth of new material about his personal life, his scientific work, and his political-social activities. Each volume has an English translation supplement.
Albert Einstein, Mileva Maric: The Love Letters, edited by Jürgen Renn and Robert Schulmann, translated by Shawn Smith. Princeton, NJ: Princeton University Press, 1992.
Einstein’s Miraculous Year: Five Papers that Changed the Face of Physics. New introduction by John Stachel; foreword by Roger Penrose. 2nd ed. Princeton, NJ: Princeton University Press, 2005. Translations of all the 1905 papers, with commentary and notes.
The New Quotable Einstein. Edited by Alice Calaprice; foreword by Freeman Dyson. Princeton, NJ: Princeton University Press, 2005.
The Political Einstein. Edited and translated by David Rowe and Robert Schulmann. Princeton, NJ: Princeton University Press, 2007.
OTHER SOURCES
Ambjorn, Jan, J. Jurkiewicz, and Renate Loll. “Quantum Gravity, or the Art of Building Spacetime.” In Approaches to Quantum Gravity, edited by Danielle Oriti Cambridge, U.K.: Cambridge University Press, 2007.Ashby, Niel. “Relativity in the Global Positioning System.” In 100 Years of Relativity Space-Time Structure, edited by Abhay Ashtekar. Hackensack, NJ: World Scientific, 2005.
Ashtekar, Abhay, ed. 100 Years of Relativity Space-Time Structure: Einstein and Beyond. Hackensack, NJ: World Scientific, 2005.
Bergmann, Peter G. “Unitary Field Theory, Geometrization of Physics or Physicalization of Geometry?” In Einstein Symposion, Berlin: aus Anlaβ der 100. Wiederkehr seines Geburtstages 25. bis 30. März 1979, edited by Horst Nelkowski, A. Hermann, and H. Poser. Lecture Notes in Physics, vol. 100. Berlin and New York: Springer, 1979.
Bičak, Jiri. “Selected Solutions of Einstein’s Field Equations: Their Role in General Relativity and Astrophysics.” Lecture Notes in Physics540 (2000): 1–126.
Brian, Denis. The Unexpected Einstein: The Real Man behind the Icon. Hoboken, NJ: Wiley, 2005.
Carter, Brandon. “Half Century of Black-Hole Theory: From Physicists’ Purgatory to Mathematicians’ Paradise.” In A Century of Relativity Physics, edited by Lysiane Mornas and Joaquin Diaz Alonso. Melville, NY: American Institute of Physics, 2006.
Damour, Thibault. “100 Years of Relativity: Was Einstein 100% Right?” In A Century of Relativity Physics, edited by Lysiane Mornas and Joaquin Diaz Alonso. Melville, NY: American Institute of Physics, 2006.
Dowker, Fay. “Causal Sets and the Deep Structure of Spacetime.” In 100 Years of Relativity Space-Time Structure, edited by Abhay Ashtekar. Hackensack, NJ: World Scientific, 2005.
Fatibene, Lorenzo, and Mauro Francaviglia, Natural and Gauge Natural Formalism for Classical Field Theories: A Geometric Perspective including Spinors and Gauge Theories. Dordrecht, Netherlands, and Boston: Kluwer, 2003.
Fölsing, Albrecht. Albert Einstein: A Biography. New York and London: Viking, 1997. Good on biographical information, weak on science.
Gambini, Rodolfo, and Jorge Pullin. “Consistent Discrete Space-Time.” In 100 Years of Relativity Space-Time Structure, edited by Abhay Ashtekar. Hackensack, NJ: World Scientific, 2005.
Goenner, Hubert F. M. “On the History of Unified Field Theories.” Living Reviews in Relativity 7 (2004). Available from http://relativity.livingreviews.org/lrr-2004-2
Hettler, Nicolaus. “Die Elektrotechnische Firma J. Einstein u. Cie in München—1876–1894.” PhD diss. Stuttgart University, 1996.
Highfield, Roger, and Paul Carter. The Private Lives of Albert Einstein. London: Faber, 1993; Boston: St, Martin's, 1994.
Janssen, Michel, John D. Norton, Jürgen Renn, et al. The Genesis of General Relativity, vol. 1: Einstein’s Zurich Notebook: Introduction and Source, vol. 2: Einstein’s Zurich Notebook: Commentary and Essays. Dordrecht, Netherlands: Springer, 2007.
Martinez, Alberto. “Handling Evidence in History: The Case of Einstein’s Wife.” Science School Review 86 (2005): 51–52.
Moszkowski, Alexander. Einstein, Einblicke in seine Gedankenwelt: Gemeinverständliche Betrachtungen über die Relativitätstheorie und ein neues Weltsystem, Entwickelt aus Gesprächen mit Einstein. Hamburg, Germany: Hoffmann und Campe, 1921.
Oriti, Daniele, ed. Approaches to Quantum Gravity. Cambridge, U.K.: Cambridge University Press, 2007.
Overbye, Dennis. Einstein in Love: A Scientific Romance. New York: Viking, 2000.
Padmanabhan, Thanu. “Understanding Our Universe: Current Status and Open Issues.” In 100 Years of Relativity Space-Time Structure, edited by Abhay Ashtekar. Hackensack, NJ: World Scientific, 2005.
Pais, Abraham. ‘Subtle is the Lord …’ The Science and the Life of Albert Einstein. New York: Oxford University Press, 1982. The best overall analysis of Einstein’s scientific work.
Pogrebin, Robin. “Love Letters by Einstein at Auction.” New York Times, 1 June 1998.
Price, Richard H. “The Physical Basis of Black Hole Astrophysics.” In 100 Years of Relativity Space-Time Structure, edited by Abhay Ashtekar.
Renn, Jürgen, and John Stachel. “Hilbert’s Foundation of Physics: From a Theory of Everything to a Constituent of General Relativity.” In The Genesis of General Relativity, vol. 3, Gravitation in the Twilight of Classical Physics: Between Mechanics, Field Theory and Astronomy, edited by Jürgen Renn and Matthias Schimmel. Dordrecht, Netherlands: Springer, 2007.
Renn, Jürgen, Tilman Sauer, and John Stachel. “The Origin of Gravitational Lensing: A Postscript to Einstein’s 1936 Science Paper.” Science 275(1997): 184–186. Reprinted in Stachel, Einstein from “B” to “Z.”
Saulson, Peter R. “Receiving Gravitational Radiation.” In 100 Years of Relativity Space-Time Structure, edited by Abhay Ashtekar.
Sayen, Jamie. Einstein in America: The Scientist’s Conscience in the Age of Hitler and Hiroshima. New York, Crown, 1985.
Schneider, Peter, Jürgen Ehlers, and Emilio E. Falco. Gravitational Lenses. Berlin and London: Springer, 1992.
Schneir, Walter. “Letter to the Editor.” New York Times, 5 June 1998.
Shimony, Abner. “Bell’s Theorem.” Stanford Encyclopedia of Philosophy(Fall 2006), edited by Edward N. Zalta. Available from http://plato.stanford.edu/archives/fall2006/entries/bell-theorem
Stachel, John. “Einstein and the Quantum: Fifty Years of Struggle.” In From Quarks to Quasars: Philosophical Problems of Modern Physics, edited by Robert Colodny. Pittsburgh, PA: University of Pittsburgh Press, 1986. Reprinted in Stachel, Einstein from “B” to “Z.” Boston, Berlin, and Basel: Birkhauser, 2002a.
———. “Einstein on the Theory of Relativity,” 1987. In Collected Papers, vol. 1, pp. 253–274. Reprinted in Stachel, Einstein from “B” to “Z.” Boston, Berlin, and Basel: Birkhauser, 2002a.
———. “Einstein’s Search for General Covariance.” In Einstein and the History of General Relativity, edited by Don Howard and John Stachel. Einstein Studies, vol. 1. Boston/Berlin/Basel: Birkhauser, 1989. Reprinted in Stachel, Einstein from “B” to “Z.” Boston, Berlin, and Basel: Birkhauser, 2002a.
———. “Einstein and Quantum Mechanics.” In Conceptual Problems of Quantum Gravity, edited by Abhay Ashtekar and John Stachel. Einstein Studies, vol. 2. Boston, Berlin, Basel: Birkhauser, 1991. Reprinted in Stachel, Einstein from “B” to “Z.” Boston, Berlin, and Basel: Birkhauser, 2002a.
———. “The Other Einstein: Einstein Contra Field Theory.” Science in Context 6(1993): 275–290. Reprinted in Stachel, Einstein from “B” to “Z.” Boston, Berlin, and Basel: Birkhauser, 2002a.
———. “Einstein and Marić: A Collaboration that Failed to Develop.” In Creative Couples in the Sciences, edited by Helena M. Pycior, Nancy G. Slack, and Pnina Abir-Am. New Brunswick, NJ: Rutgers University Press, 1996. Reprinted in Satchel, Einstein from “B” to “Z.” Boston, Berlin, and Basel: Birkhauser, 2002a.
———. “Einstein’s Light Quantum Hypothesis, or Why Didn't Einstein Propose a Quantum Gas a Decade-and-a-Half Earlier?” In Einstein: The Formative Years, 1879–1909, edited by Don Howard and John Stachel. Boston: Birkhauser, 2000. Reprinted in Einstein from “B” to “Z.” Boston, Berlin, and Basel: Birkhauser, 2002a.
———. Einstein from “B” to “Z. ” Boston, Berlin, and Basel:
Birkhauser, 2002a.
———. “The First Two Acts,” 2002b. In Einstein from “B” to “Z.” Boston, Berlin, and Basel: Birkhauser, 2002a.
———. “The Young Einstein: Poetry and Truth,” 2002c. In Einstein from “B” to “Z.” Boston, Berlin, and Basel: Birkhauser, 2002a.
———. “Fresnel’s (Dragging) Coefficient as a Challenge to 19th Century Optics of Moving Bodies.” In The Universe of General Relativity, edited by A. J. Cox and Jean Einsenstaedt. Einstein Studies, vol. 11. Boston, Basel, Berlin: Birkhauser, 2005a.
———. “Introduction to the Centenary Edition,” 2005b. In Einstein’s Miraculous Year: Five Papers that Changed the Face of Physics. New introduction by John Stachel; foreword by Roger Penrose. 2nd ed., 2005b. Princeton, NJ: Princeton University Press, 2005.
———. “The Story of Newstein: Or Is Gravity Just Another Pretty Force?” In The Genesis of General Relativity, vol. 4, Gravitation in the Twilight of Classical Physics: The Promise of Mathematics, edited by Jürgen Renn and Matthias Schimmel. Berlin: Springer, 2007.
Will, Clifford. “Was Einstein Right? Testing Relativity at the Centenary.” In 100 Years of Relativity Space-Time Structure, edited by Abhay Ashtekar. Hackensack, NJ: World Scientific, 2005.
Winteler-Einstein, Maja. “Albert Einstein—Beitrag für Sein Lebensbild,” 1924. In Collected Papers, vol. 1.
Zubirini, Xavier. “La idea de naturaleza: la nueva fisica.” Translation in Nature, History, God. Washington, DC: University Press of America, 1981.
John Stachel
"Einstein, Albert."
Complete Dictionary of Scientific Biography.
2008.
Encyclopedia.com.
9 Dec. 2014
<http://www.encyclopedia.com>.
Loading...
martes, 2 de diciembre de 2014
Como programar un microcontrolador Atmel usbtiny
https://www.sparkfun.com/tutorials/93
Beginning Embedded Electronics - 2
Lecture 2 - How to Get Code Onto a Microcontroller
You can get all the parts for this lecture here.
We also highly recommend that you get a multimeter with a 'continuity'
setting. A good quality multimeter with this setting goes for ~$60 and
as high as $300 for a really spectacular one. We like our $60 cheapo.
Sorry for the confusion. When these tutorials were written and photographed, we used the ATmega8. We now carry the newer ATmega328. You will find all ATmega328 information in the following pages, but the pictures will show an ATmega8.
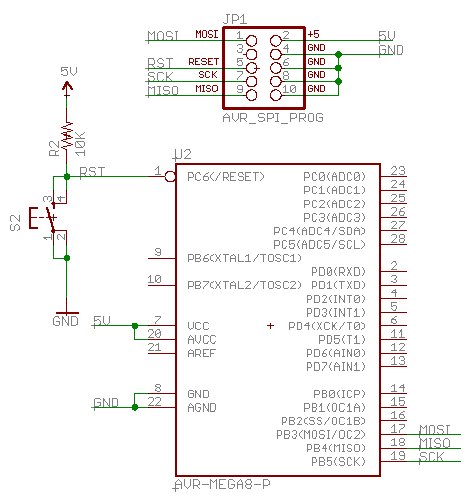
I'm assuming you've got your 5V supply tested and working. Next, we need to insert the ATmega into the breadboard and connect up power and ground.

Note: The 5V 'rail' is the horizontal row of holes next to the red line. You should have a wire connecting your 5V power regulator circuit to one hole on the 5V rail. This will energize all the holes next to the red line with 5V. This is true about the blue line as well. All the horizontal holes next to the blue line are connected together. One of these holes should be connected to the ground pin on your voltage regulator, and to the ground connection of your wall wart. You can connect the VCC pins on the ATmega328 to any holes along the 5V rail, and you connect the GND pins on the ATmega328 to any hole along the blue GND rail.
Oh, hey! If no one ever told you, there is a really simple way to figure out where pin 1 is on an IC. The manufacturer of anything polarized (tantalum caps, electrolytic caps, LEDs, ICs, etc) will always put some sort of marking on the device to indicate the how the device is supposed to be oriented. For ICs, there is a small dimple on one end of the IC. The blue arrow in the picture is pointing to this dimple. The orange arrow points at pin 1, and the blue labels show how the pin numbers increase.

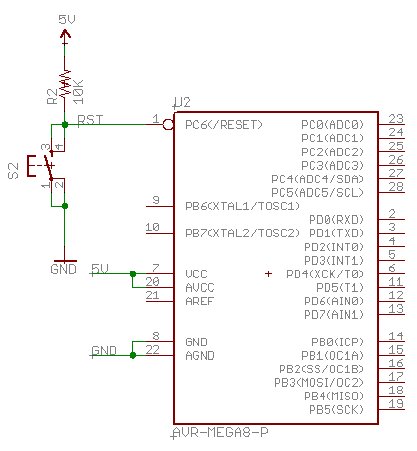
Actually this is not wholly true - there is one more connection that needs to be made before the ATmega328 starts running code. The RESET pin on the ATmega328 needs to be connected to VCC. You can either wire the RESET pin directly to 5V or you can 'tie it high' by connecting the RESET pin to VCC through a resistor. This will allow you to add a momentary reset button. What's this? The reset line on the ATmega328 is exactly what it sounds like - it resets the micro just like the reset works on your computer. If you look at the ATmega328 datasheet you'll see the RESET label is written with a line above it. This is nomenclature that indicates the reset pin is active low. What is 'active low'? The RESET pin is an input. A low level on this pin will put the micro into reset - i.e. the pin is activated with a low input, aka 'active low'. So unless you want your ATmega328 to stay in reset, you'll need to pull this pin high.
Now you need a reset button. A momentary switch is a switch that is activated (or closed) while you're touching it and open when you release the button. These are often called 'tactile switches' because they 'click' when you depress them giving the person pressing the button some 'tactile' feedback.





Sorry for the confusion. When these tutorials were written and photographed, we used the ATmega8. We now carry the newer ATmega328. You will find all ATmega328 information in the following pages, but the pictures will show an ATmega8.
I'm assuming you've got your 5V supply tested and working. Next, we need to insert the ATmega into the breadboard and connect up power and ground.

ATmega8 (works the same with ATmega168, and 328) straddling the middle row of the breadboard
You will need to slightly bend in the legs of the DIP
(dual inline package) to get the ATmega to straddle the breadboard
center. Be careful! Do not bend the pins too far inward. The pins of the
ATmega should insert into the inner two most rows on the breadboard. I
find it best to to insert one side and then slightly push the IC
sideways until the other side of pins can insert into the opposite row
on the breadboard. Confusing, I know.Note: The 5V 'rail' is the horizontal row of holes next to the red line. You should have a wire connecting your 5V power regulator circuit to one hole on the 5V rail. This will energize all the holes next to the red line with 5V. This is true about the blue line as well. All the horizontal holes next to the blue line are connected together. One of these holes should be connected to the ground pin on your voltage regulator, and to the ground connection of your wall wart. You can connect the VCC pins on the ATmega328 to any holes along the 5V rail, and you connect the GND pins on the ATmega328 to any hole along the blue GND rail.
Oh, hey! If no one ever told you, there is a really simple way to figure out where pin 1 is on an IC. The manufacturer of anything polarized (tantalum caps, electrolytic caps, LEDs, ICs, etc) will always put some sort of marking on the device to indicate the how the device is supposed to be oriented. For ICs, there is a small dimple on one end of the IC. The blue arrow in the picture is pointing to this dimple. The orange arrow points at pin 1, and the blue labels show how the pin numbers increase.

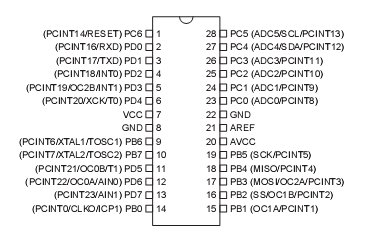
Pin labeling on an IC
Counting from the dimple, pin 1 is on the left and increases
down the left side of the IC. The pin numbers jump to the right side row
of pins and count up. See image from the ATmega328 datasheet below.
The ATmega328 should be in the breadboard, pin 7 (VCC) and pin
20 (AVCC) should be connected to your 5V rail and pins 8 and 22 (GND)
should be connected to GND on your bread board. If you turn your power
circuit on, the ATmega328 is now running, but it has nothing to run!Actually this is not wholly true - there is one more connection that needs to be made before the ATmega328 starts running code. The RESET pin on the ATmega328 needs to be connected to VCC. You can either wire the RESET pin directly to 5V or you can 'tie it high' by connecting the RESET pin to VCC through a resistor. This will allow you to add a momentary reset button. What's this? The reset line on the ATmega328 is exactly what it sounds like - it resets the micro just like the reset works on your computer. If you look at the ATmega328 datasheet you'll see the RESET label is written with a line above it. This is nomenclature that indicates the reset pin is active low. What is 'active low'? The RESET pin is an input. A low level on this pin will put the micro into reset - i.e. the pin is activated with a low input, aka 'active low'. So unless you want your ATmega328 to stay in reset, you'll need to pull this pin high.
Now you need a reset button. A momentary switch is a switch that is activated (or closed) while you're touching it and open when you release the button. These are often called 'tactile switches' because they 'click' when you depress them giving the person pressing the button some 'tactile' feedback.

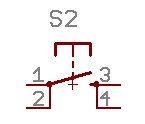
This is what the schematic part looks like. Notice pins 1 and 2
are connected together. 3 and 4 are connected together. And when you
press 'de button, it temporarily connects 1/2+3/4 together.

Notice this button has five legs. If your button has five legs,
just ignore the middle leg - it's not connected to anything and can be
clipped off.
To test this button, whip out the trusty multimeter and set it
to the continuity setting. This is the setting on nicer, mid-grade
multimeters that is crucial to troubleshooting and experimenting. Touch
the probes together - you should hear a tone indicating that there is
continuity or a (nearly) zero resistance path between the probes. Insert
the button into the breadboard and probe the two pins on one side of
the button. If you picked pins 1/2 or 3/4 you should hear a tone. These
pins are permanently connected inside switch. If you picked pins 1/3 or
2/4, you won't hear a noise - but hit the button. By hitting the button
you will make an electrical connection between all four pins - and you
should hear the tone! This means you have electrical continuity.

The schematic shows pins 1 and 2 of the reset switch connected
together (connected to ground) and pins 3/4 connected together
(connected to !RESET) . In practice, you just need the switch to work.
Play with your multimeter and find two pins that don't make noise when
the button is not touched, and do make noise when the button is
depressed. Use these two pins.
The schematic shown above is what we're going for. The 10K
resistor 'pulls' the reset pin high during normal activity. By pulling
the reset pin high, the ATmega328 runs normally. When you push the reset
switch (S2), the reset pin sees a continuous connection to ground.
Since the resistance through the depressed switch is nearly zero, it
wins (compared to the resistance of the 10K resistor!) and the reset pin
is pulled low, RESET is activated and the ATmega328 goes into reset.
Release the button and the reset pin is pulled high again and the
ATmega328 comes out of reset. Nifty!

ATmega328 pinout
See the dimple from the ATmega328 datasheet? Looking at the top
of the IC (legs down), with the dimple to the top, pin numbers increase
starting from 1 in the top left corner. This is how every IC pin is
numbered. However, the orientation marking varies a bit between
manufacturers and between packaging types. Look for a non-congruent
marking like a dimple, small dot, white arrow, a notched corner -
anything that makes that area of the chip different from the other parts
of the chip probably indicates pin 1. When in doubt, check the
datasheet.

Reset wired next to a ATmega8 (same applies for the ATmega168, and ATmega328)
Learn how to use the the continuity setting on your multimeter. It will be vital to troubleshooting down the road!
Each microcontroller manufacturer has a different method to get
code in the flash memory of the micro. In the past few years there has
been emphasis placed on ISP or "in system programming". ISP allows you
to program the IC without having to disconnect the microcontroller from
the application. This is not trivial! History was much more painful.
Atmel has designed a relatively straight forward method that requires
the control of a few pins (6 total). Because of this simple interface,
the hardware programmer that is required to connect your computer to
this ISP interface is very straight forward (cheap!) as well.

The red stripe indicates the location of Pin 1
Remember how we identified pin1 on the IC from the dimple? Well
connectors also need polarization so that we don't reverse the
orientation of the connector and fry things. Unfortunately the way
connectors are numbered is opposite that of ICs. In the picture of the
ISP connector, you see the red stripe indicating pin 1. An IC counts
sequentially down one side. Connectors on the other hand, increase pin
numbers, back and forth, as you work your way down the connector.
The programming chain looks something like this:
-
There is a free C compiler called AVR-GCC. User writes code in C and then compiles that code into HEX files
-
AVR-GCC can be installed on the Windows platform with an easy WinAVR install program
-
The user gets this HEX code onto an AVR via the ISP pins
-
Both a serial port programmer and a parallel port programmere have been designed to connect the computer port to the AVR ISP pins
-
The computer runs a command line program to transfer the HEX file from the computer, to the serial or parallel port, and out to the AVR ISP pins
-
The micro runs the machine code (*.HEX files) once powered or reset
What's a C compiler?
This is a program that inputs a program written in the C language and
outputs a HEX file. We prefer to program in C because it is easier for
us than assembly and more flexible than BASIC.
What's a HEX file?
This is a file that contains various hexidecimal characters. These hex
'codes' represent machine instructions that the ATmega328 understand.
This file is what gets sent down to the programmer, and the programmer
loads these machine instructions onto the ATmega328.
Before we can get too crazy, download and install WinAVR
on the computer that you will be doing your code development on. If
this link goes out of date, a google search should take you straight to
it. The windows install should be fairly straight forward - follow all
the defaults. WinAVR contains a version of the GCC compiler and various
other tools including avrdude and Programmer's Notepad. avrdude is a
simple command line program that takes a HEX file and sends it to the
serial or parallel port for programming onto an Atmel microcontroller.
Working backwards up this list, I'll provide you with an example
'Hello World' HEX file that will prove that everything is working
correctly on your micro. With any micro controller board, the first
trick is always to get an LED to blink. This is the 'Hello World' of
embedded systems. Guess what blink_1MHz.hex does?
With the blink hex file in hand, you now need to get it onto the
micro. You will need to connect the AVR-PG1 (or the AVR-PG2) to the
ATmega328. The easiest way to do this is with 9 wires running from your
breadboard to the 10-pin connector on the ISP connector on the
AVR-PG1/PG2.

Jamming wires into the ISP connector is not a good long-term
solution but for the sake of getting the LED to blink, it'll do. I've
cut short wires and stripped both ends. One stripped end is inserted
into the end of the black programming connector, the other end is
inserted into the breadboard.

The AVR-PG2 parallel programmer wired into the ATmega328. I've
also wired up two 0.1uF caps. These decoupling caps are placed near the
VCC and GND pins on the ATmega328 to help reduce noise into the IC. You
may think you have a straight DC 5V but not really - these 0.1uF caps
help reduce ripple on the 5V line. Yes, the ATmega328 will probably run
without them but they're good to have installed.
AVR ISP Note: You really do have to wire all 4 GND pins. You cannot wire just one of the GND pins on the ISP connector.
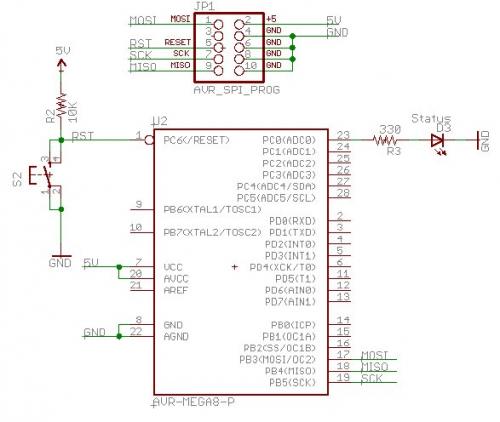
Additionally we need an LED to control. This can be tied to any GPIO pin. PC0 looks like a good spot.

The resistor/LED order does not matter - just remember (from
Tutorial 1) that you must have the resistor! The GPIO pin doesn't
actually matter. blink_1MHz.hex will toggle all the pins on all ports so
you can hook the resistor to any pin. As you add more peripheral
hardware you will want to dedicate some pins for alternate use (such as
TX and RX pins for serial communication).
You're getting closer! Time to program the chip!
Once WinAVR is installed, you should have a few new icons on
your desktop. Programmers Notepad is a nice code editor and highlighter.
What's a code editor/highlighter? When programming, you will
need a text editor on your computer so that you can create (type) code.
Once you've created this 'code' on your computer (inside the code
editor) you will pass this code to the compiler (you will click a button
that runs the compiler with the C file you've typed) and the compiler
will create a HEX file (assuming there are no problems or typos in your
code). The highlighter? When creating code, it's often nice to have
various parts of your program color coded so that you can tell a common
things like for( ) and #define. This highlighting helps a lot when programming.
Use whichever text tool you like. Notepad will work, but is pretty rudimentary. I also like JFE
from my PIC days. Both have a 'tools' option which is great but JFE is
better in my opinion because it lists the C functions that you can
double click on and navigate to. If there is a way to do a similar trick
in Programmer's Notepad 2, please let me know! Because Programmers
Notepad v2 (aka PN2) comes with the WinAVR installation, we'll use it!
AVR-GCC is extremely powerful, very complex, and difficult to
use initially. I am used to passing a *.c file to a PIC compiler (CC5x)
and getting a HEX file back out. No fuss, no mess. Believe you me, the
pain of getting AVR-GCC up and running is worth it. AVR-GCC is a truly
nice compiler, and it's free. I've included a stock Makefile and blink_1MHz.c file in blink_1MHz.zip
to get you started. I am by no means a Linux or make type of person.
All you need to know is that when you type 'make' at the command prompt,
the compiler is going to look for a file called 'Makefile' (no file
extension!) and use that file to direct how to compile your C file.

These are the only two files you should need to get blink to
compile. Open up blink_1MHz.c in programmer's notepad and click on
Tools->Make All. This is the same as typing 'make all' from the
command prompt from what ever directory you saved these two files. For
example
C:\Code\Blink>make all
should compile your code as well. It's just a bit easier to do
this through the Programmer's Notepad interface rather than toggling
back and forth to the Command Prompt window. Once you have successfully
compiled the C file into a HEX file, you now need to get that hex file
onto the AVR. It's finally time to power up your system! The cheap AVR
programmers require the target (that's your breadboard) to provide power
to the programmer (that's the AVR-PG1 or PG2). Power up your bread
board - you should see the power LED come on. From here on out, I will
assume you're using the AVR-PG2 parallel port programmer.
There is only two spots in the makefile that you should be
concerned about at this time. These two spots are located under the
programming options section. This makefile is huge, but scroll down to
the Programming Options (avrdude) section. Now put a '#' in front of
lines you want to comment out.
If you're using the AVR-PG1 (serial port programmer) you edit like this:
#AVRDUDE_PROGRAMMER = stk200
AVRDUDE_PROGRAMMER = ponyser
# com1 = serial port. Use lpt1 to connect to parallel port.
#AVRDUDE_PORT = lpt1
AVRDUDE_PORT = COM1
If you're using the AVR-PG2 (parallel port programmer) you edit like this:
AVRDUDE_PROGRAMMER = stk200
#AVRDUDE_PROGRAMMER = ponyser
# com1 = serial port. Use lpt1 to connect to parallel port.
AVRDUDE_PORT = lpt1
#AVRDUDE_PORT = COM1
Of course the port numbers depend on your specific computer but
once you get things working, you'll be set for life. Assuming you've
edited and saved your makefile, go back to PN2. With your breadboard
powered, click Tools->Program. This will send the command 'make
program' to the command prompt. If everything is setup correctly, you
should have successfully loaded blink_1MHz.hex onto your target
ATmega328 and your LED should be blinking.
If you get an error :
can't open device "giveio"
Then read this page. Basically you need to copy the giveio.sys file from C:\WinAVR/bin to the C:\Windows directory, then type install_giveio.bat at the command prompt.
Typical Problems:
If you still are not able to program the AVR - this is where 99% of first time users end up. Dig in and troubleshoot.
Are the ISP connections correct? It's easy to get the ISP connector backwards. Take a look at the photos above.
Is there a loose wire? Pull out the multimeter and check that
you've got 5V being delivered to the VCC and GND pins on the ATmega328.
Do the wires going into the ISP connector have a good solid connection?
Do you have your ATmega328 connected to both power and ground?
Is your 5V supply outputting 5V?
Do you have the right COM port or LPT port selected in your makefile?
There is a multitude of things to check. It's hard! I know. But
once you get things correctly set up, and that LED blinks - it will feel
fantastic!
Ok - I'm going to assume that you got the code correctly loaded
onto the AVR and that the LED is blinking. Congratulations! You are now
well on your way to a whole world of pain! Once you get one thing
working, it's hard to stop! GPS, datalogging, RF, PCB layout - it's all
just a couple hops away.
You can get all the parts for this lecture here.
Here are some additional resources for AVR programming:
We love feedback! Please report typos, comments, or recommendations to spark@sparkfun.com.
Lecture 1 - Background and Power Supply
Lecture 2 - How to Get Code Onto a Microcontroller
Lecture 3 - What is an oscillator?
Lecture 4 - UART and Serial Communication
Lecture 5 - AVR GCC Compiling
Lecture 6 - Soldering Basics
Lecture 7 - SMD Soldering
Lecture 8 - Eagle: Schematics
Lecture 9 - Eagle: PCB Layout
Lecture 10 - Eagle: Creating a new part
Lecture 2 - How to Get Code Onto a Microcontroller
Lecture 3 - What is an oscillator?
Lecture 4 - UART and Serial Communication
Lecture 5 - AVR GCC Compiling
Lecture 6 - Soldering Basics
Lecture 7 - SMD Soldering
Lecture 8 - Eagle: Schematics
Lecture 9 - Eagle: PCB Layout
Lecture 10 - Eagle: Creating a new part
Installing an Arduino Bootloader
https://learn.sparkfun.com/tutorials/installing-an-arduino-bootloader
Installing an Arduino Bootloade
Contributors:
 M-Short
M-Short
Overview
Do you have a bricked Arduino that won’t accept code anymore? Or, maybe you wrote your own firmware and would like to upload it to your Arduino? Or, maybe you just want to learn more about the inner-workings of Arduino, AVR, and microcontrollers in general. Well, you’re in luck! This tutorial will teach you what a bootloader is, why you would need to install/reinstall it, and go over the process of doing so.Suggested Reading
You may want to check out these tutorials before continuing down the bootloader path.What is a Bootloader?
Atmel AVRs are great little ICs, but they can be a bit tricky to program. You need a special programmer and some fancy .hex files, and its not very beginner friendly. The Arduino has largely done away with these issues. They’ve put a .hex file on their AVR chips that allows you to program the board over the serial port, meaning all you need to program your Arduino is a USB cable.The bootloader is basically a .hex file that runs when you turn on the board. It is very similar to the BIOS that runs on your PC. It does two things. First, it looks around to see if the computer is trying to program it. If it is, it grabs the program from the computer and uploads it into the ICs memory (in a specific location so as not to overwrite the bootloader). That is why when you try to upload code, the Arduino IDE resets the chip. This basically turns the IC off and back on again so the bootloader can start running again. If the computer isn’t trying to upload code, it tells the chip to run the code that’s already stored in memory. Once it locates and runs your program, the Arduino continuously loops through the program and does so as long as the board has power.
Why Install a Bootloader
If you are building your own Arduino, or need to replace the IC, you will need to install the bootloader. You may also have a bad bootloader (although this is very rare) and need to reinstall the bootloader. There are also cases where you’ve put your board in a weird setting and reinstalling the bootloader and getting it back to factory settings is the easiest way to fix it. We’ve seen boards where people have turned off the serial port meaning that there is no way to upload code to the board, while there may be other ways to fix this, reinstalling the bootloader is probably the quickest and easiest. Like I said, having a bad bootloader is actually very very rare. If you have a new board that isn’t accepting code 99.9% of the time its not the bootloader, but for the 1% of the time it is, this guide will help you fix that problem.Selecting a Programmer
We are going to talk about 2 different types of programmers you can use to install or reinstall bootloaders.Option 1: Dedicated Programmers
For a quick easy programmer we recommend looking into the AVR Pocket Programmer (Windows only).Or, you can use the official Atmel AVR MKII programmer.
The AVR Pocket Programmer or most cheaper options will work just fine for most applications, but they may have problems with some boards, specifically ones with lots of memory like the ATMega2560 based boards.
Option 2: Using the Arduino as a Programmer
The other option is grabbing an Arduino Uno (or Duemilanove). If you go into the Arduino IDE you will see an example sketch called ‘Arduino as ISP.’ If you upload this code to your Arduino, it will basically act as an AVR programmer. This isn’t really recommended for production of boards, or boards with lots of memory, but, in a pinch, it works pretty well. Also as of this writing the code only works on ATmega328 boards. Maybe one day it will work on the Leonardo or Due, but not yet.Connecting the Programmer
In-Circuit Serial Programming (ICSP)
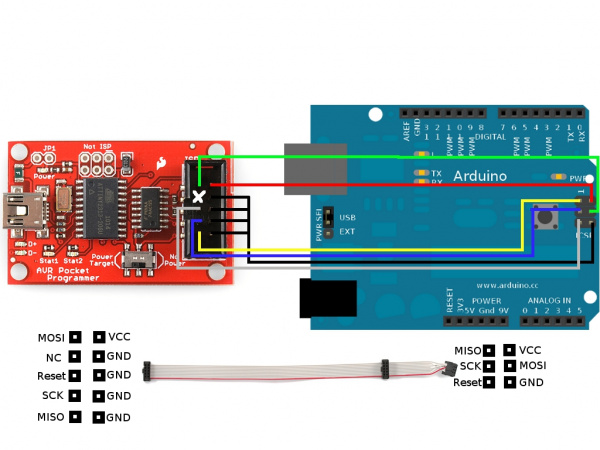
It’s very uncommon to program ICs before they are soldered onto a PCB. Instead, most microcontrollers have what’s called an in-system programming (ISP) header. Particularly, some IC manufacturers, such as Atmel and Microchip, have a specialized ISP method for programming their ICs. This is referred to as in-circuit serial programming (ICSP) Most Arduino and Arduino compatible boards will have a 2x3 pin ICSP header on them. Some may even have more than one depending on how many ICs live on the PCB. It breaks out three of the SPI pins (MISO, MOSI, SCK), and power, ground, and reset. These are the pins you’ll need to connect your programmer to in order to reflash the firmware on your board.
Here we have the Arduino Uno R3. It
has two ICSP headers: one for the ATmega16U2 and one for the ATmega328.
To reflash the bootloader on this board, you would use just the ICSP
header for the ATmega328.
On some smaller boards you may not see this connector, but the pins should be broken out elsewhere. Whether you’re using an SMD IC or a DIP IC,
the ISP pins should be accessible in one form or another. Some boards
might only have test points for the ISP header. If this is the case, you
may want to consider getting an ISP Pogo Adapter. This kit allows you to temporarily make a good connection with test test points in order to reprogram your IC.
ISP Pogo Adapter Kit Fully Assembled. You can connect any of the programmers we mentioned in the previous section to this board.
If you are having trouble finding the ICSP pins on your particular Arduino board, you can consult this website for detailed pinouts of most Arduino related ICs and then some.Once you have located the six ICSP pins on your board, it’s time to hook up your programmer to the board. You can use a programming cable to connect the two, or, if you don’t have a cable, you can just use some male-to-female jumper wires.
If you are using a programmer such as the MKII or the Pocket Programmer, your setup should look something like this:
Click for larger image.
Or, if you’re using the Arduino as your programmer, it should look like this:
Click for larger image.
Here’s a table to help clarify which connections go where.| Arduino as ISP | AVR Programmer | ISP Header | ATmega328 | ATmega32U4 |
| Vcc/5V | 5V | Pin 2 | Vcc | Vcc |
| GND | GND | Pin 6 | GND | GND |
| MOSI/D11 | MOSI | Pin 4 | D11 | D16 |
| MISO/D12 | MISO | Pin 1 | D12 | D14 |
| SCK/D13 | SCK | Pin 3 | D13 | D15 |
| D10 | Reset | Pin 5 | Reset | Reset |
Uploading Code - Easy Way
The easy way to upload the bootloader involves using the Arduino IDE. Open your IDE select the board you want to program. Then select the programmer (if you are using the Arduino as ISP you will also need to select the COM port that the Arduino as ISP is connected to). Then select BurnBootloader. This will take the board you selected and look up the associated bootloader in the board.txt file. Then, it will find the bootloader in the bootloader folder and install it. This only works if the board is installed correctly in the IDE and you have the correct bootloader.If for some reason you want to use a bootloader that isn’t installed in the Arduino IDE, visit the nest section. However, it’s probably easier to just install the bootloader from the Arduino IDE. For those who are curious about settings such as fuse bits, have no fear. Arduino takes care of all the messy details for you when you burn bootloaders through it.
Uploading Code - Hard Way
The hard way is for those people who want to use the command line. This method may be more preferable if you are modifying and recompiling and don’t want to have to keep updating the IDE, but otherwise its pretty unnecessary. Again you will need to get the programmer, and hook everything up. In this example we are using avrdude on Windows.There are two steps to this process. The first step involves setting the fusebits. Fusebits are the part of the AVR chip that determine things like whether you are using an external crystal or whether you want brown out detection. The commands listed below are for the Arduino Uno using an ATMega328, they will probably work on some other similar boards such as the Duemilanove, but make sure you know what you are doing before playing with fusebits (NOTE: these fusebits will not work on a 3.3V/8MHz board). All the required fuse bits are listed in the boards.txt file for different boards, but again, if you have a boards.txt file installed then just use the Easy Way.
Arduino as ISP:
avrdude -P comport -b 19200 -c avrisp -p m328p -v -e -U efuse:w:0x05:m -U hfuse:w:0xD6:m -U lfuse:w:0xFF:mAVR Pocket Programmer:
avrdude -b 19200 -c usbtiny -p m328p -v -e -U efuse:w:0x05:m -U hfuse:w:0xD6:m -U lfuse:w:0xFF:mThe second step is actually uploading the program.
Arduino as ISP:
avrdude -P comport -b 19200 -c avrisp -p m328p -v -e -U flash:w:hexfilename.hex -U lock:w:0x0F:m
AVR Pocket Programmer: avrdude -b19200 -c usbtiny -p m328p -v -e -U flash:w:hexfilename.hex -U lock:w:0x0F:mOne last bit of info. As we stated earlier, a bootloader is essintially a .hex file. Thus, you can use this method to upload and code you wish to your ICs.
Resources and Going Further
For more info on AVRs, bootloaders, and flashing firmware to other boards, check out these other great tutorials.- AVRDUDE
- Bootloader info from Arduino
- Arduino as ISP
- Pinouts for Various ICs and Development Boards
- Getting started with the Pocket Programmer