Definition 1: A QR factorization (or QR decomposition) of a square matrix A consists of an orthogonal matrix Q and an upper triangular matrix R such that A = QR.
Property 1 (QR Factorization): For any n × n invertible matrix A, we can construct a QR factorization.
Proof: Let
A1, …, An represent the columns of
A. Since
A is invertible, we know that
A1, …, An are independent and forms a basis for the set of all
n × 1 column vectors. We can therefore we can use the Gram-Schmidt process to construct an orthonormal basis
Q1, …, Qn for the set of all
n × 1 column vectors. Let
Q be the
n ×
n matrix whose columns are
Q1, …, Qn. By Property 4 of
Orthogonal Vectors and Matrices,
Q is an orthogonal matrix, and so by Property 6 of
Orthogonal Vectors and Matrices,
QTQ = I.
We seek a matrix
R such that
A = QR. Since
QTQ = I, it follows that
QTA = QTQR = R, and so we conclude that
R = QTA is the required matrix. Let
R = [
rij], and so
rij =
Qi · Aj. As we saw in the proof of Theorem 1 of
Orthogonal Vectors and Matrices, each
Qi can be expressed as a linear combination of
A1, …, Ai, which means that
rij = 0 for
i > j, which shows that
R is an upper triangular matrix. It is also easy to show by induction that
rij > 0 for each
i.
Observation: We can extend Property 1 to certain non-square matrices. The proof is similar and Q and R are constructed in the same way.
Property 2 (QR Factorization): For any m × n matrix A with rank (A) = n ≤ m , we can construct an m × n orthonormal matrix Q and an n × n upper triangular matrix R such that A = QR.
Observation: Shortly we will show
how to use the QR Factorization to calculate eigenvalues and
eigenvectors, and in fact we will show a better way to produce such a QR
Factorization, which is less prone to rounding errors.
For now we show how to use QR factorization to find the solution to
AX = C, the problem studied in
Determinants and Linear Equations. First we note that since
A = QR and
Q is orthogonal, if
AX = C, then
C = AX = QRX and so
QTC = QTQRX = RX. Thus
RX = QTC. But since
R
is an upper triangular matrix all of whose diagonal elements are
non-zero (actually they are positive), we can use backwards substitution
to find the solution for
X. In fact if
R =[
rij],
X = [
xj] and
QTC = [
bi], then we will have a series of equations of the form (looking from the bottom up):
The first equation can be used to find the value of x1. Substituting this value for x1 in the second equation enables you find x2. Continuing in this manner you can find xn-1. Substituting these values in the last equation enables you to find xn.
Example 2: Solve the following system of linear equations using QR Factorization
We could solve this problem using
Gaussian elimination, as can be seen from Figure 2 where the array
formula =ELIM(U4:X7) in range U10:X13 produces the solution x = -0.34944, y = 0.176822 and z = 0.792727.
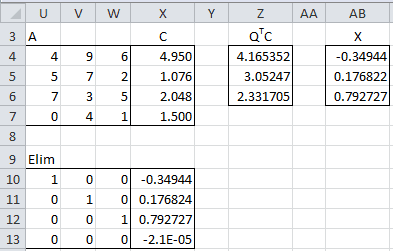
Figure 1 – Solving AX = C using QR Factorization
We now show how to find a solution using QR factorization. First we calculate
QTC (range Z4:Z6) as =MMULT(TRANSPOSE(I4:K7),X4:X7) using the values for
Q shown in Figure 1 of
Orthogonal Vectors and Matrices. We next calculate the values for
X (range AB4:AB6) via backwards substitution using the formulas in Figure 2.
Figure 2 – Formulas in Figure 1
Definition 2: A Householder matrix A is a square matrix for which there exists a vector V such that VTV = I and A = I – 2VVT.
Property 3: A Householder matrix is orthogonal
Proof: Let
A be a Householder matrix. First we show that
A is symmetric, as follows:
We next show that A2 = I, from which it follows that AAT = A2 = I, which by definition means that A is orthogonal.
Observation: We already showed
how to generate a QR factorization for any matrix using the Gram-Schmidt
procedure. Unfortunately, for practical purposes this procedure is
unstable, in the sense that as it is applied on a computer, round off
errors accumulate and so while theoretically a valid QR factorization is
obtained, in practice the results can sometimes be wrong.
We now present a procedure for
constructing a QR factorization, using Householder matrices, which is
more stable. As we did previously, we start with the case of a square
matrix.
Property 4: Every invertible square matrix A has a QR factorization. Furthermore there is an efficient algorithm for finding this QR factorization.
Define Vk = [vi] by
vi = 0 for i < k
Define
Pk =
I – 2
VkVkT,
Qk =
PkQk-1 and
Rk+1 = PkRk.
Now define
R = Rn and
Q =
Qn-1T.
Definition 3: The QR factorization procedure for finding the eigenvalues/vectors of a square matrix is as follows:
Let
Q and
R be defined as above. Let
A0=
A,
Q0=
Q and
R0 =
R. Define
Ak+1 =
RkQk. Since
Ak+1 is also invertible it has a QR decomposition
Ak+1 =
Qk+1Rk+1.
Property 5: If the eigenvalues of A are distinct and non-zero then Ak converges to an upper triangular matrix with the same eigenvalues as A. If A is symmetric then Ak converges to a diagonal matrix with the same eigenvalues as A.
Observation: Since the eigenvalues of an upper triangular matrix are found on the diagonal, this means that for k sufficiently large the eigenvalues of A are found on the diagonal of Ak.
Example 3: Use the QR decomposition method to find the eigenvalues of
![\left[\begin{array}{ccc} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \end{array}\right]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_uuvuMPY6fQIbzKczNhASe0fVnh5BA4ka8csH8dSVbZS7rsh2f_Ifj1XytrtFHeJWZgXfg6odj7Tj-Dpca-nV1XIsNy-4XW159kcsRVm07-1wQwvm6cxpnLsDHe3GhtgQyvREfCgJiz3AzEfURCsfFm5JTM4FvLpe3i7EhQUDblzO310XE4qGvQKqaNUxHUn1-0dcmGfezTVe7d9P2sJUVMTHbdOHGpd1lxX1aNiIG8Cak-KOFLvP9ufxBtUb4ehinMGegbTiiCQrsRLZLRWbSQ8uP2BLppV5E=s0-d "\left[\begin{array}{ccc} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \end{array}\right]")
We begin by finding
Q and
R.
Figure 3 – QR Factorization using a Householder matrix (step 1)
Thus
where A = QR, R is an upper triangular matrix and QTQ = I. Calling A0 = A, R0 = R and Q0 = Q, we now define a new A = RQ (i.e. A1 = R0Q0) and repeat the process.
Figure 4 – QR Factorization using a Householder matrix (step 2)
The result is a new R and Q, which we now call R1 and Q1 such that A1 = Q1R1, R1 is an upper triangular matrix and Q1TQ1 = I. As before we now define a new A, i.e. A2 = R1Q1 and repeat the process. We continue this process until we get an Ak which is sufficiently close to being a diagonal matrix.
We now skip to the 9th iteration where
A has now converged to a diagonal matrix:
Figure 5 – QR Factorization using a Householder matrix (step 9)
Thus
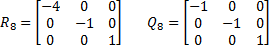
and so
Thus the eigenvalues of the original matrix
A are 4, 1 and 1.
Once you find an eigenvalue you can use
the Gaussian Elimination Method to find the corresponding eigenvectors
since these are solutions to the homogeneous equation (
A – λI)
X = 0, which can be solved as described in Definition 5 of
Determinants and Linear Equations.
The only problem with this approach is when the eigenvalues of a matrix
are not all distinct (such as in Example 3). Gaussian elimination can
find one such eigenvector, but not a set of orthogonal eigenvectors (one
for each instance of the repeated eigenvectors, as is required in
Example 3).
A better approach is to use the fact that the corresponding eigenvectors are the columns of the matrix B = Q0Q1…Qk (where k is the iteration where Ak is sufficiently close to a diagonal matrix). For Example 3 we define B0 = Q0 and Bn+1 = BnQn (shown as B′Q
in K32:M34 of Figure 4 and K214:M216 of Figure 5. Thus we conclude that
the eigenvectors corresponding to 4, 1, 1 are the columns in the matrix
Since the process described above is
complicated and tedious to carry out, it is simpler and faster to use
the following supplemental functions eVALUES and eVECTORS as described
in
Eigenvalues and Eigenvectors.
Example 4: Use the eVECTORS supplemental function to find the eigenvalues and eigenvectors for Example 3.
The output from eVECTORS(A6:C8) is shown in Figure 6.
Figure 6 – Calculating eigenvalues/vectors using eVECTORS
which is the same result we obtained previously.
Observation: We can extend Property 4 to certain non-square matrices. The proof is similar and Q and R are constructed in the same way.
Property 6 (QR Factorization): For any m × n matrix A with rank(A) = n ≤ m, we can construct in an efficient way an m × n orthonormal matrix Q and an n x n upper triangular matrix R such that A = QR.
Since the process described above is
complicated and tedious to carry out, it is simpler and faster to use
the following supplemental functions to create a QR factorization of a
matrix.
Real Statistics Functions: The Real Statistics Resource Pack provides the following supplemental array functions, where R1 is a m × n range in Excel
QRFactorR(R1): Produces the n × n array R for which A = QR where A is the matrix in R1. Note that to obtain Q you use the fact that Q = AR-1; i.e. Q is obtained using the formula =MMULT(R1, MINVERSE(R2)) where range R2 contains the formula QRFactorR(R1).
QRFactor(R1): Produces an m+n × n array. The first m rows of the output is Q and the next n rows of the output is R where A = QR and A is the matrix in range R1.
You can optionally specify what is
considered zero in the algorithm used to calculate these functions. The
default is 0, but it may be acceptable to use some other small value
(e.g. 0.00001) as sufficiently small to be considered to be zero. To
specify this value you use QRFactorR(R1, prec) and QRFactorQ(R1, prec). If the prec parameter is not used then it defaults to 0, and so QRFactorR(R1) = QRFactorR(R1, 0).
Example 5: Find the QR factorization of the matrix in range A4:D9 of Figure 7
Figure 7 – QR Factorization
R (range F4:I7) is calculated by the array formula =QRFactorR(A4:D9) and Q (range F10:I14) by =MMULT(A4:D9,MINVERSE(F4:I7)). Both Q and R (range K4:N13) can be calculated by =QRFactor(A4:D9).
As you can see from the figure,
QTQ = I and so
Q is orthogonal and
A = QR.
Real Statistics Functions: As we
saw in Example 2, QR Factorization can be used to solve a system of
linear equations. The approach described above can be extended to invert
a matrix. The Real Statistics Resource Pack provides the following two
supplemental functions to automate these processes.
QRSolve(R1, R2) – assuming R1 is an m × n range describing matrix A and R2 is an m × 1 range describing the column vector C, QRSolve outputs an n × 1 column vector X containing the solution to AX = C
QRInverse(R1) = inverse of the matrix described by range R1 (assumes that R1 is a square matrix)
Observation: Referring to Figure 1, QRSolve(U4:W7, X4:X7) would output the result described in AB4:AB7.
Example 6: Find the inverse of the matrix in range W18:Y20 of Figure 8 using QRInverse.
Figure 8 – Matrix inversion using QR Factorization
Using QRInverse(W18:Y20), you obtain the
results shown in range AA18:AC20. This is the same result as obtained
using MINVERSE(W18:Y20).
Real Statistics Data Analysis Tool: The
Matrix data analysis tool contains a
QR Factorization option that computes the QR factorization of the matrix in the Input Range. See Figure 3 of
Matrix Operations for an example of the use of this tool.
en algunos valores que se
localicen, por ejemplo, desde la fila 3 hasta la fila 6 de la
columna B, nos situamos en una celda en la que nos interese dejar
el resultado de dicha evaluación y se digita 
en Excel la sintaxis es: 
, en Excel se escribe 