Calculating Capacitor Current in Transformerless Power Supplies

Transformer less AC to DC power supply circuit using dropping capacitor

Jaseem vp / July 19, 2012

http://www.circuitsgallery.com/2012/07/transformer-less-ac-to-dc-capacitor-power-supply-circuit2.html

Production of low voltage DC power supply from AC power is the most important problem faced by many electronics developers and hobbyists. The straight forward technique is the use of a step down transformer to reduce the 230 V or 110V AC to a preferred level of low voltage AC. But i-St@r comes with the most appropriate method to create a low cost power supply by avoiding the use of bulky transformer.Yes, you can construct power supply for your development without a transformer. This circuit is so simple and it uses a voltage dropping capacitor in series with the phase line. Transformer less power supply is also called as capacitor power supply. It can generate 5V, 6V, 12V 150mA from 230V or 110V AC by using appropriate zener diodes. See the design below.

Circuit diagram

Components required

1. Resistors (470kΩ, 1W; 100Ω)
2. Capacitors (2.2µF, 400V, X rated; 1000µF, 50V)
3. Bridge rectifier (1N4007 diodes x 4)
4. Zener diode (6.2V, 1W)
5. LED (Optional)

Working of Transformer less capacitor power supply

• This transformer less power supply circuit is also named as capacitor power supply since it uses a special type of AC capacitor in series with the main power line.

• A common capacitor will not do the work because the mains spikes will generate holes in the dielectric and the capacitor will be cracked by passing of current from the mains through the capacitor.

• X rated capacitor suitable for the use in AC mains is vital for reducing AC voltage.

• A X rated dropping capacitor is intended for 250V, 400V, 600V AC. Higher voltage versions are also obtainable. The dropping capacitor is non polarized so that it can be connected any way in the circuit.

• The 470kΩ resistor is a bleeder resistor that removes the stored current from the capacitor when the circuit is unplugged. It avoid the possibility of electric shock.

• Reduced AC voltage is rectifiered by bridge rectifier circuit. We have already discussed about bridge rectifiers. Then the ripples are removed by the 1000µF capacitor.

• This circuit provides 24 volts at 160 mA current at the output. This 24 volt DC can be regulated to necessary output voltage using an appropriate 1 watt or above zener diode.

• Here we are using 6.2V zener. You can use any type of zener diode in order to get the required output voltage.

Design

Reactance of the capacitor,
where f is the supply frequency and C is the capacitance.
If the supply frequency is 50Hz, then reactance of 2.2µF X rated capacitor is given by,

So output current,

You can design your own supply if you need high current rating other than 159mA by choosing different capacitor values.

Calculating Capacitor Current in Transformerless Power Supplies

https://www.homemade-circuits.com/calculating-capacitor-current-in/

Last Updated on November 18, 2017 by Swag 76 Comments

You may have studied countless transformerless power supplies in this blog and in the web, however calculating the crucial mains capacitor current in such circuits has always remained an issue for the many constructors.

Analyzing a Capactive Power Supply

Before we learn the formula for calculating and optimizing the mains capacitor current in a transformerless power supply, it would be important to first summarize a standard transformerless power supply design.
The following diagram shows a classic transformerless power supply design:

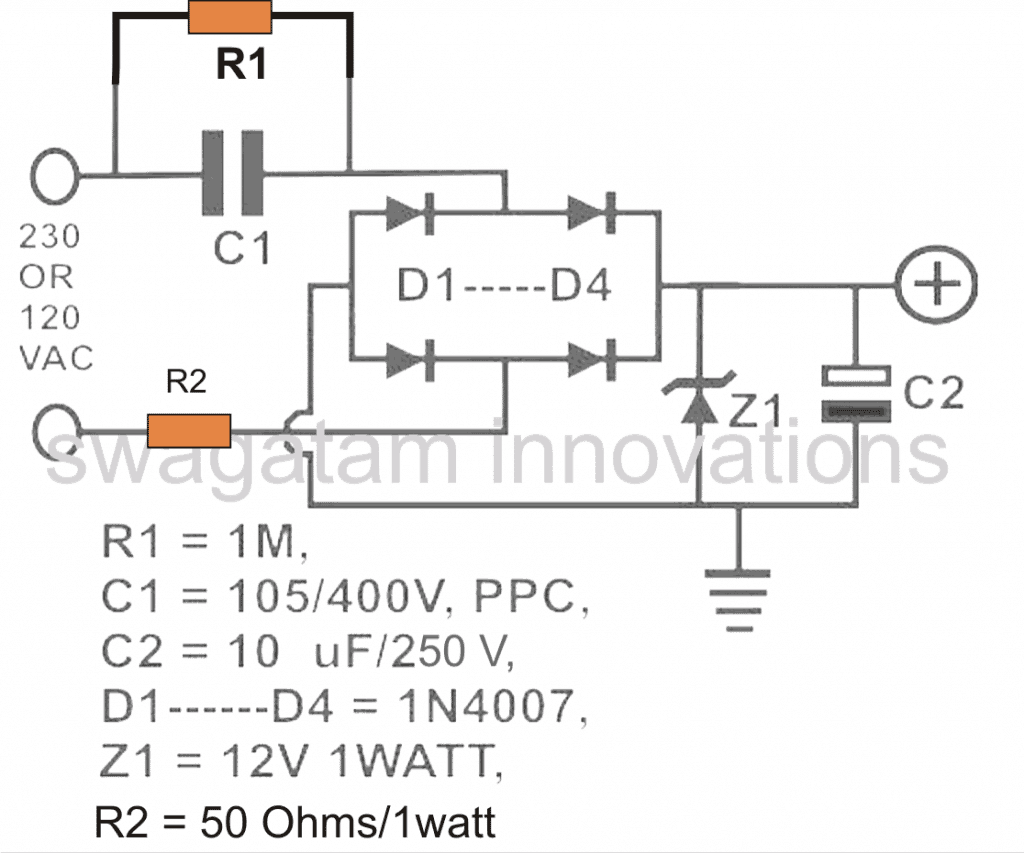
Referring to the diagram, the various components involved are assigned with the following specific functions:
C1 is the nonopolar high voltage capacitor which is introduced for dropping the lethal mains current to the desired limits as per the load specification. This component thus becomes extremely crucial due to the assigned mains current limiting function.
D1 to D4 are configured as a bridge rectifier network for rectifying the stepped down AC from C1, in order to make the output suitable to any intended DC load.
Z1 is positioned for stabilizing the output to the required safe voltage limits.
C2 is installed to filter out any ripple in the DC and to create a perfectly clean DC for the connected load.
R2 may be optional but is recommended for tackling a switch ON surge from mains, although preferably this component must be replaced with a NTC thermistor.

Capacitor Controls Current

In the entire transformerless design discussed above, C1 is the one crucial component which must be dimensioned correctly so that the current output from it is optimized optimally as per the load specification.
Selecting a high value capacitor for a relatively smaller load may increase the risk of excessive surge current entering the load and damaging it sooner.
A properly calculated capacitor on the contrary ensures a controlled surge inrush and nominal dissipation maintaining adequate safety for the connected load.

Using Ohm's Law

The magnitude of current that may be optimally permissible through a transformerless power supply for a particular load may be calculated by using Ohm's law:
I = V/R
where I = current, V = Voltage, R = Resistance
However as we can see, in the above formula R is an odd parameter since we are dealing with a capacitor as the current limiting member.
In order to crack this we need to derive a method which will translate the capacitor's current limiting value in terms of Ohms or resistance unit, so that the Ohm's law formula could be solved.

Calculating Capacitor Reactance

To do this we first find out the reactance of the capacitor which may be considered as the resistance equivalent of a resistor.
The formula for reactance is:
Xc = 1/2(pi) fC
where Xc = reactance,
pi = 22/7
f = frequency
C = capacitor value in Farads
The result obtained from the above formula is in Ohms which can be directly substituted in our previously mentioned Ohm's law.
Let's solve an example for understanding the implementation of the above formulas:
Let's see how much current a 1uF capacitor can deliver to a particular load:
We have the following data in our hand:
pi = 22/7 = 3.14
f = 50 Hz (mains AC frequency)
and C= 1uF or 0.000001F
Solving the reactance equation using the above data gives:
Xc = 1 / (2 x 3.14 x 50 x 0.000001)
=  3184 ohms approximately
Substituting this equivalent resistance value in our Ohm's law formula, we get:
R = V/I
or I = V/R
Assuming V = 220V (since the capacitor is intended to work with the mains voltage.)
We get:
I = 220/3184
= 0.069 amps or 69 mA approximately
Similarly other capacitors can be calculated for knowing their maximum current delivering capacity or rating.
The above discussion comprehensively explains how a capacitor current may be calculated in any relevant circuit, particularly in transformerless capacitive power supplies.




https://circuitdigest.com/electronic-circuits/transformerless-power-supply

X-Rated Capacitor

As mentioned they are connected in series with phase line of AC to lower down the voltage, they are available in 230v, 400v, 600v AC or higher ratings.

Below is the table for output current and output voltage (without the Load), of different values of X-rated capacitors:

Capacitor Code	Capacitor value	Voltage	Current
104k	0.1 uF	4 v	8 mA
334k	0.33 uF	10 v	22 mA
474k	0.47 uF	12 v	25 mA
684k	0.68 uF	18 v	100 mA
105k	1 uF	24 v	40 mA
225k	2.2 uF	24 v	100 mA

Selection of voltage dropping capacitor is important, it is based on Reactance of Capacitor and  the amount of current to be withdrawn. The Reactance of the capacitor is given by below formula:

X = 1 / 2¶fC

X = Reactance of Capacitor

f = frequency of AC

C = Capacitance of X rated capacitor

We have used 474k means 0.47uF capacitor and frequency of AV mains is 50 Hz so the Reactance X is:

X = 1 / 2*3.14*50*0.47*10^-6 = 6776 ohm (approx)

Now we can calculate the current (I) in the circuit:

I = V/X = 230/6775 = 34mA

So that’s how the Reactance and Current is calculated.

Como trabajar con un LCD con modulo I2C en Arduino en 3 pasos para un LCD 20x4 ( o 16x2)

Como trabajar con un LCD con modulo I2C en Arduino en 4 pasos para un LCD 20x4 ( o 16x2)

Paso 1. Alambrar el modulo I2C al Arduino UNO
SDA - Pin A4 de Arduino
SCL - Pin A4 de Arduino
VCC - Fuente Arduino
GND - Tierra Arduino

Paso 2. Escanear la dirección del módulo con el siguiente código

//Descargado de:
//https://miarduinounotieneunblog.blogspot.com.co/2015/12/display-lcd-16x2-con-comunicacion-i2c.html

/*  TITULO: Escaner de direcciones I2C

    AUTOR:
   
    MARIANO DEL CAMPO GARCÍA (@2016) --> INGENIERO TÉCNICO INDUSTRIAL ESPECIALIDAD ELECTRÓNICA
    - FACEBOOK: https://www.facebook.com/mariano.delcampogarcia
    - TWITTER: https://twitter.com/MarianoCampoGa
    - CORREO: marianodc83@gmail.com
   
   
    DESCRIPCIÓN DEL PROGRAMA
   
    Este programa sirve para buscar la dirección de comunicación I2C, en dispositivos conectados a nuestro
    Arduino mediante este protocolo de comunicación. El programa nos envía todas las direcciones de los
    dispositivos I2C que tengamos conectados en un determinado instante a través del monitor serie del IDE
    de Arduino. En este caso vamos a utilizar el escaner I2C para encontrar la dirección de un display LCD
    1602 conectado a través de este protocolo de comunicación.
 

    ESQUEMA DE CONEXION
   
                                      +-----+
         +----[PWR]-------------------| USB |--+
         |                            +-----+  |
         |         GND/RST2  [ ][ ]            |
         |       MOSI2/SCK2  [ ][ ]  A5/SCL[ ] |   SCL del módulo I2C conectado al LCD 1602
         |          5V/MISO2 [ ][ ]  A4/SDA[ ] |   SDA del módulo I2C conectado al LCD 1602
         |                             AREF[ ] |
         |                              GND[ ] |
         | [ ]N/C                    SCK/13[ ] |  
         | [ ]IOREF                 MISO/12[ ] |  
         | [ ]RST                   MOSI/11[ ]~|  
         | [ ]3V3    +---+               10[ ]~|  
         | [ ]5v    -| A |-               9[ ]~|  
         | [ ]GND   -| R |-               8[ ] |  
         | [ ]GND   -| D |-                    |
         | [ ]Vin   -| U |-               7[ ] |  
         |          -| I |-               6[ ]~|  
         | [ ]A0    -| N |-               5[ ]~|  
         | [ ]A1    -| O |-               4[ ] |  
         | [ ]A2     +---+           INT1/3[ ]~| 
         | [ ]A3                     INT0/2[ ] |  
         | [ ]A4/SDA  RST SCK MISO     TX>1[ ] |  
         | [ ]A5/SCL  [ ] [ ] [ ]      RX<0[ ] |  
         |            [ ] [ ] [ ]              |
         |  UNO_R3    GND MOSI 5V  ____________/
          \_______________________/

  NOTAS:
   - La alimentación y la masa del módulo LCM 1602 I2C V1 instalado en el LCD 1602, van directamente conectadas
     a VCC (+5V) y GND respectivamente. 
*/

// Librería necesaria para comunicación I2C
#include <Wire.h>


void setup()
{
  Wire.begin(); // Iniciamos la comunicación I2C

  Serial.begin(9600); // Iniciamos la comunicación con el monitor serie
  //while (!Serial);             // Leonardo: wait for serial monitor
  Serial.println("\nEscaner de direcciones I2C");
}


void loop()
{
  byte error, address;
  int nDevices;

  Serial.println("Escaneando...");

  nDevices = 0;
  for(address = 1; address < 127; address++ )
  {
    // Se utiliza el valor de retorno de Write.endTransmisstion() para ver si se ha reconocido
    // o no la dirección I2C de un dispositivo
  
    Wire.beginTransmission(address);
    error = Wire.endTransmission();

    if (error == 0)
    {
      Serial.print("Dispositivo I2C encontrado en la direccion 0x");
      if (address<16)
        Serial.print("0");
      Serial.print(address,HEX);
      Serial.println("!");

      nDevices++;
    }
    else if (error == 4)
    {
      Serial.print("Error desconocido en la direccion 0x");
      if (address<16)
        Serial.print("0");
      Serial.println(address,HEX);
    }   
  }
  if (nDevices == 0)
    Serial.println("No se han encontrado direcciones I2C de ningun dispositivo \n");
  else
    Serial.println("Hecho\n");

  delay(5000);           // Espera 5 segundos hasta el siguiente escaneo
}


Paso 3. Descargar la libreria desde Github, e instalarla en Arduino (Programa -> Incluir Libreria...)

https://github.com/fdebrabander/Arduino-LiquidCrystal-I2C-library


 https://cloud.mail.ru/public/4q5r/YzCuu7hEW

Paso 4. Hola mundo del LCD con I2C
Tener en cuenta escribir la dirección del escaneo en la creación del objeto: lcd(0x3F, 20, 4), en este caso el escaneo nos arrojo 0x3f



#include <Wire.h>
#include <LiquidCrystal_I2C.h>

// Set the LCD address to 0x3F for a 16 chars and 2 line display
LiquidCrystal_I2C lcd(0x3F, 20, 4);

void setup()
{
  // initialize the LCD
  lcd.begin();

  // Turn on the blacklight and print a message.
  lcd.backlight();
  lcd.print("Hello, world!");
}

void loop()
{
  // Do nothing here...
}



Otro enlace interesante:
http://osoyoo.com/2017/01/15/use-arduino-serial-port-to-talk-with-i2c-lcd-display/

Programa en LAbVIEW para guardar la adquisición de 2 señales en un archivo plano txt

Programa en LAbVIEW 2017 para guardar la adquisición de 2 señales en un archivo plano txt










https://cloud.mail.ru/public/GF8d/dA4EDDoCY

Las columnas del archivo dados.txt son:

Tiempo: contador i, se multiplica por el Sampled Period, si se quiere hacer analisis en excel
Señal 1: Una señal aleatoria de 0 a 100
Señal 2: Otra señal aleatoria de 0 a 100

Aplicacion en LabVIEW para comunicacion Serial y Guardar en archivo de Excel

Aplicacion en LabVIEW para comunicacion Serial y Guardar en archivo de Excel
-Comunicación serial (VISA se debe descargar e instalar)
-Aplicación con 4 leds
-Escritura en un archivo de excel


Enlaces version Labview 2017 y código Arduino
https://cloud.mail.ru/public/MGAc/qZq8TPUgh

En version LabVIEW 2015
https://cloud.mail.ru/public/AzM9/nLwqzFso3

A continuación se presentan algunos pantallazos del programa en LabVIEW, en Arduino y el archivo de Excel que se escribe

Labview 2017 Full 1 link y todos sus módulos

LabVIEW 2017

 https://drive.google.com/drive/folders/0B8WW70Y4DPUqYVd0QlZHQnJBem8

  https://www.youtube.com/watch?v=vFue-b9WS7Q

Labview 2017 Full 1 link y todos sus módulos

 

http://softwareparaingenieros.com/labview-2017/

 

 

 

book Blender Game Engine Beginner's Guide The non programmer's guide to creating 3D video games Victor Kuller Bacone

Buena página para descargar libro

Blender Game Engine
Beginner's Guide
The non programmer's guide to creating 3D video games
Victor Kuller Bacone

https://it-book.pro/download/?id=126&type=pdf

Programación Visual Basic (VBA) para Excel y Análisis Numérico

https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/NUMERICO/excel/

 

Programación Visual Basic (VBA) para Excel y Análisis Numérico

M.Sc. Walter Mora F., M.Sc. José Luis Espinoza B.
Escuela de Matemática
Instituto Tecnológico de Costa Rica

• Introducción
• Evaluación de funciones
  • Funciones definidas por el usuario
  • Errores comunes
  • Evaluando una función en varios tipos de parámetros
    • Evaluación con argumentos variables
    • Evaluación con argumentos variables y/o constantes
    • Construyendo rangos con un incremento fijo
  
  
• Gráficas
• Programación de macros
  • Introducción
    • Editar y ejecutar macros.
  • Funciones
    • Ejemplo 1: implementar una función.
    • Ejemplo 2: lectura de parámetros en celdas
  
  
• Elementos de programación en VBA
  • Flujo secuencial
  • Flujo condicional (If - Else)
  • Flujo repetitivo (For-Next, While-Wend)
  • Manejo de rangos
  • Subrutinas. Edición y ejecución de una subrutina
  • Ejecución de una subrutina mediante un botón
  • Matrices dinámicas
  • Inclusión de procedimientos de borrado
  
  
• Evaluando expresiones matemáticas escritas en lenguaje matemático común
  • Usando clsMathParser. Sintaxis.
  • Ejemplo: un graficador de funciones 2D y un graficador de superficies 3D
  • Ejemplo: series numéricas y series de potencias
  • Ejemplo: método de Newton-Raphson
  • Ejemplo: método de Romberg para integración
  • Ejemplo: la función Gamma
  • Ejemplo: cuadratura gaussiana e integral doble gaussiana.
    • Cuadratura gaussiana.
    • Integral doble gaussiana.
  
  
• Bibliografía
• archivo.pdf | archivo.zip

A good Page http://www.gregthatcher.com/

A good Page
http://www.gregthatcher.com/

Linear Algebra

• Gauss-Jordan Elimination Calculator
• Calculate Pivots
• Factorize into A=LU
• Inverse Matrix Calculator
• Null Space Calculator
• Left Null Space Calculator
• Column Space Calculator
• Row Space Calculator
• Multiply Two Matrices

Redes Neuronales en Python
http://pybrain.org/

Welcome to PyBrain

PyBrain is a modular Machine Learning Library for Python. Its goal is to offer flexible, easy-to-use yet still powerful algorithms for Machine Learning Tasks and a variety of predefined environments to test and compare your algorithms.
PyBrain is short for Python-Based Reinforcement Learning, Artificial Intelligence and Neural Network Library. In fact, we came up with the name first and later reverse-engineered this quite descriptive "Backronym".

How is PyBrain different?

While there are a few machine learning libraries out there, PyBrain aims to be a very easy-to-use modular library that can be used by entry-level students but still offers the flexibility and algorithms for state-of-the-art research. We are constantly working on more and faster algorithms, developing new environments and improving usability.

What PyBrain can do

PyBrain, as its written-out name already suggests, contains algorithms for neural networks, for reinforcement learning (and the combination of the two), for unsupervised learning, and evolution. Since most of the current problems deal with continuous state and action spaces, function approximators (like neural networks) must be used to cope with the large dimensionality. Our library is built around neural networks in the kernel and all of the training methods accept a neural network as the to-be-trained instance. This makes PyBrain a powerful tool for real-life tasks.

Using PyBrain

PyBrain is open source and free to use for everyone (it is licensed under the BSD Software Licence). Just download it and start using the algorithms and modules in your own project or have a look at the provided tutorials and examples. If you use PyBrain for your research, we kindly ask you to cite us in your publications. Use the reference below or import this bibtex reference.

http://robologs.net/2016/02/29/tutorial-de-arduino-y-blender/

Tutorial de Arduino y Blender

Posted on February 29, 2016 by Gl4r3

Nota: es recomendable tener unos conocimientos básicos de como funciona la interfaz de Blender para seguir bien el tutorial.
Animaciones, edición de video, videojuegos, realidad virtual… lo que más me gusta de Blender es que permite hacer de todo. Para los que no conozcáis Blender, se trata de una suite de creación 3D con la que se puede hacer modelaje, rigging, VFX, composición e incluso videojuegos. Los usuarios más avanzados pueden crear scripts en Python para hackear personalizar la aplicación a su gusto.

Hoy voy a enseñaros una parte de Blender de la que pocas veces se habla: la posibilidad de recibir datos a través del puerto de serie. Usaremos esta característica para recibir datos de una placa Arduino y mover un objeto en Blender.
Así que poned buena música y empezamos.

---

1- Instalar Blender

La última versión de Blender puede bajarse desde la página de descargas de blender.org. En el momento de redactar este tutorial, la versión que tengo es la 2.76. Descargad Blender, descomprimid el archivo y recordad cuál es su directorio.
Un par de apuntes para los que estéis en Linux: os recomiendo que no os bajéis la versión de Blender que hay en los repositoros de vuestra distribución. A mi no me ha dejado utilizar la librería pySerial, mientras la versión que he descargado de blender.org no me ha dado problemas.
Por otra parte, en Linux hay que ejecutar Blender en modo superusuario para poder utilizar el puerto de serie. Para hacerlo, abrid la Terminal dentro de la carpeta donde tengáis Blender y escribid:

sudo ./blender

Este es el splash screen de la v2.76.

---

2- pySerial y Blender

Blender lleva por defecto muchas librerías que podemos aprovechar para nuestros proyectos. Pero la librería pySerial no está, y habrá que instalarla. Por suerte, Blender es muy configurable y podemos hacerlo sin problema.
Lo primero es descargar la librería pySerial desde aquí y descomprimir el .tar.gz . Dentro de la carpeta que aparece después de la extracción, hay otra carpeta llamada “serial”. Hay que copiarla dentro de la carpeta de Blender->2.76->python->lib->python3.4
Este es mi path al directorio donde hay que copiar la carpeta “serial”:

Ahora, ¿cómo puede uno estar seguro de haber seguido bien todos los pasos? Abrid Blender. Arriba, en la barra de información hay un menú desplegable con distintas configuraciones para la pantalla. Pulsad la que pone Scripting.


La configuración del espacio de trabajo cambiará a esta:

La parte de abajo (esa ventana negra con el texto azul) es la consola de Python de Blender. Funciona como una consola de Python normal, sólo que en vez de utilizar las librerías Python del sistema usa las de Blender.
Si tecleáis “import serial” en la consola y no da ningún error, es que la librería pySerial se ha instalado bien.

La librería pySerial está lista

Pero si aparece algún mensaje de error, tendréis que revisar todos los pasos hechos hasta ahora.

---

3- Código de Arduino

El ejemplo más sencillo que se me ocurre es mover un cubo de Blender con Arduino.
Este programa envía por serial el mensaje 0.1 para que el cubo avance, y -0.1 para que retroceda.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

void setup() {    Serial.begin(9600); }     void loop() {    for(int i = 0; i < 100; i++)    {       Serial.print("&0.1"); Serial.print("\n");       delay(10);    }       for(int i = 0; i < 100; i++)    {       Serial.print("&-0.1"); Serial.print("\n");       delay(10);    } }

Si habéis leído el código, veréis que al principio de cada mensaje he puesto el carácter “&”. A veces, Blender no lee bien los strings que le llegan por Serial y cambia su contenido. Este “&” sirve como detector de errores: cuando escribamos el script en python para el Blender Game Engine, vamos a hacer que ignore cualquier mensaje que no empiece por este carácter.

---

4- Código de Blender

Vamos a colocar un script python al cubo que viene por defecto en la escena, para que se mueva según lo que llegue por serial.
Primero habrá que cambiar la configuración del espacio de trabajo a Game Logic. Id al desplegable de la barra de información y seleccionad la opción “Game Logic“.


La configuración de la pantalla cambiará a esta:

También cambiad el motor de Blender Render a Blender Game:

La ventana gris de arriba a la derecha es un editor de texto. Aquí es dónde vamos a programar el script en python para leer el puerto serial. Como no quiero que perdáis la vista, colocad el cursor sobre el editor de texto y pulsad Ctrl+Flecha Arriba para hacer grande la ventana.

*crujido de dedos* Vamos allá

Cread un nuevo script pulsando el botón “New” que hay en la barra de abajo, y cambiadle el nombre a “main.py”. Ahora copiad el script de abajo en el editor. ¡Eh, pero no tan rápido! Antes cambiad el “/dev/ttyUSB0” de la línea 6 por la dirección de vuestra placa Arduino.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

import serial #Comunicacion Serial import bge #Funciones propias de blender   #Abrimos el puerto serial ser = serial.Serial("/dev/ttyUSB0", 9600)     #Guardamos el controlador que esta ejecutando este script cont = bge.logic.getCurrentController()   #Buscamos el propietario del controlador (el cubo) obj = cont.owner   a = ser.readline() #Leer hasta el final de linea \n a = a.decode("ascii") #Decodificar la linea   if a[0] == "&" and len(a) >= 4:    a = a[1:] #Eliminamos el detector de errores    a = a[:-1] #Eliminamos el final de linea    obj.applyMovement([float(a),0,0], False) #Movemos el cubo     ser.close()

Comprobad que todos los tabuladores hayan quedado bien.
Cuando tengáis copiado el código habrá que asignarlo al cubo. Pulsad Ctrl+Flecha abajo para volver el editor de texto a su tamaño original.
Con el cubo seleccionado con el botón derecho, Id a la ventana de Game Logic Editor y añadid un sensor de tipo always. Activad el TRUE level triggering y poned Skip a 0.

Configuración del sensor Always

Después, hay que añadir un controlador de tipo “python”. Cambiad el nombre del script a main.py:


Por último, hay que juntar el Sensor Always con el Controlador Python. Para hacerlo, pulsad el círculo negro que hay a la derecha del sensor con el Botón Izquierdo del ratón y arrastrad hasta el anillo que hay a su derecha.

5- Probar el “juego”

Con Arduino conectado a través de USB a vuestro ordenador, si situáis el cursor encima de la escena 3D (dónde está el cubo) y pulsáis la tecla “P”, veréis como el Cubo se mueve de un lado a otro.
Espero que este tutorial os haya servido. Si tenéis dificultades en algún paso, podéis escribirme un comentario y os echaré una mano. ¡Hasta la próxima!

Runge-Kutta (RK4) numerical solution for Differential Equations

https://www.intmath.com/differential-equations/12-runge-kutta-rk4-des.php

12. Runge-Kutta (RK4) numerical solution for Differential Equations

In the last section, Euler's Method gave us one possible approach for solving differential equations numerically.
The problem with Euler's Method is that you have to use a small interval size to get a reasonably accurate result. That is, it's not very efficient.
The Runge-Kutta Method produces a better result in fewer steps.

Runge-Kutta Method Order 4 Formula

Applications of RK4

Mechanics

• Springs and dampeners on cars (This spring applet uses RK4.)

Biology

• Predator-prey models
• Fisheries collapses
• Drug delivery
• Epidemic prediction

Physics

• Climate change models
• Ozone protection

Aviation

• On-board computers
• Aerodynamics

$\displaystyle{y}{\left({x}+{h}\right)}$y(x+h) $\displaystyle={y}{\left({x}\right)}+$=y(x)+ $\displaystyle\frac{1}{{6}}{\left({F}_{{1}}+{2}{F}_{{2}}+{2}{F}_{{3}}+{F}_{{4}}\right)}$61​(F1​+2F2​+2F3​+F4​)

where

$\displaystyle{F}_{{1}}={h} f{{\left({x},{y}\right)}}$F1​=hf(x,y)
$\displaystyle{F}_{{2}}={h} f{{\left({x}+\frac{h}{{2}},{y}+\frac{{F}_{{1}}}{{2}}\right)}}$F2​=hf(x+2h​,y+2F1​​)
$\displaystyle{F}_{{3}}={h} f{{\left({x}+\frac{h}{{2}},{y}+\frac{{F}_{{2}}}{{2}}\right)}}$F3​=hf(x+2h​,y+2F2​​)
$\displaystyle{F}_{{4}}={h} f{{\left({x}+{h},{y}+{F}_{{3}}\right)}}$F4​=hf(x+h,y+F3​)

Where does this formula come from?

Here's a brief background to the formula.

Formula derivation

We learned earlier that Taylor's Series gives us a reasonably good approximation to a function, especially if we are near enough to some known starting point, and we take enough terms.
However, one of the drawbacks with Taylor's method is that you need to differentiate your function once for each new term you want to calculate. This can be troublesome for complicated functions, and doesn't work well in computerised modelling.
Carl Runge (pronounced "roonga") and Wilhelm Kutta (pronounced "koota") aimed to provide a method of approximating a function without having to differentiate the original equation.
Their approach was to simulate as many steps of the Taylor's Series method but using evaluation of the original function only.

Runge-Kutta Method of Order 2

We begin with two function evaluations of the form:

$\displaystyle{F}_{{1}}={h} f{{\left({x},{y}\right)}}$F1​=hf(x,y)
$\displaystyle{F}_{{2}}={h} f{{\left({x}+\alpha{h},{y}+\beta{F}_{{1}}\right)}}$F2​=hf(x+αh,y+βF1​)

The $\displaystyle\alpha$α and $\displaystyle\beta$β are unknown quantities. The idea was to take a linear combination of the $\displaystyle{F}_{{1}}$F1​ and $\displaystyle{F}_{{2}}$F2​ terms to obtain an approximation for the $\displaystyle{y}$y value at $\displaystyle{x}={x}_{{0}}+{h}$x=x0​+h, and to find appropriate values of $\displaystyle\alpha$α and $\displaystyle\beta$β.
By comparing the values obtains using Taylor's Series method and the above terms (I will spare you the details here), they obtained the following, which is Runge-Kutta Method of Order 2:

$\displaystyle{y}{\left({x}+{h}\right)}={y}{\left({x}\right)}+\frac{1}{{2}}{\left({F}_{{1}}+{F}_{{2}}\right)}$y(x+h)=y(x)+21​(F1​+F2​)

where

$\displaystyle{F}_{{1}}={h} f{{\left({x},{y}\right)}}$F1​=hf(x,y)
$\displaystyle{F}_{{2}}={h} f{{\left({x}+{h},{y}+{F}_{{1}}\right)}}$F2​=hf(x+h,y+F1​)

Runge-Kutta Method of Order 3

As usual in this work, the more terms we take, the better the solution. In practice, the Order 2 solution is rarely used because it is not very accurate.
A better result is given by the Order 3 method:

$\displaystyle{y}{\left({x}+{h}\right)}=$y(x+h)= $\displaystyle{y}{\left({x}\right)}+\frac{1}{{9}}{\left({2}{F}_{{1}}+{3}{F}_{{2}}+{4}{F}_{{3}}\right)}$y(x)+91​(2F1​+3F2​+4F3​)

where

$\displaystyle{F}_{{1}}={h} f{{\left({x},{y}\right)}}$F1​=hf(x,y)
$\displaystyle{F}_{{2}}={h} f{{\left({x}+\frac{h}{{2}},{y}+\frac{{F}_{{1}}}{{2}}\right)}}$F2​=hf(x+2h​,y+2F1​​)
$\displaystyle{F}_{{3}}={h} f{{\left({x}+\frac{{{3}{h}}}{{4}},{y}+\frac{{{3}{F}_{{2}}}}{{4}}\right)}}$F3​=hf(x+43h​,y+43F2​​)

This was obtained in a similar way to the earlier formula, by comparing Taylor's Series results.
The most commonly used Runge-Kutta formula in use is the Order 4 formula (RK4), as it gives the best trade-off between computational requirements and accuracy.

Get the Daily Math Tweet!
IntMath on Twitter

Let's look at an example to see how it works.

Example

Use Runge-Kutta Method of Order 4 to solve the following, using a step size of $\displaystyle{h}={0.1}$h=0.1 for $\displaystyle{0}\le{x}\le{1}$0≤x≤1.

$\displaystyle\frac{{\left.{d}{y}\right.}}{{\left.{d}{x}\right.}}=\frac{{{5}{x}^{2}-{y}}}{{e}^{{{x}+{y}}}}$dxdy​=ex+y5x2−y​
$\displaystyle{y}{\left({0}\right)}={1}$y(0)=1

Step 1

Note: The following looks tedious, and it is. We'll use a computer (not calculator) to do most of the work for us. The following is here so you can see how the formula is applied.
We start with $\displaystyle{x}={0}$x=0 and $\displaystyle{y}={1}$y=1. We'll find the $\displaystyle{F}$F values first:
$\displaystyle{F}_{{1}}={h} f{{\left({x},{y}\right)}}$F1​=hf(x,y) $\displaystyle={0.1}\frac{{{5}{\left({0}\right)}^{2}-{1}}}{{e}^{{{0}+{1}}}}$=0.1e0+15(0)2−1​ $\displaystyle=-{0.03678794411}$=−0.03678794411
For $\displaystyle{F}_{{2}}$F2​, we need to know:

$\displaystyle{x}+\frac{h}{{2}}={0}+\frac{0.1}{{2}}={0.05}$x+2h​=0+20.1​=0.05, and
$\displaystyle{y}+\frac{{F}_{{1}}}{{2}}$y+2F1​​ $\displaystyle={1}+\frac{{-{0.03678794411}}}{{2}}$=1+2−0.03678794411​ $\displaystyle={0.98160602794}$=0.98160602794

We substitute these into the $\displaystyle{F}_{{2}}$F2​ expression:
$\displaystyle{F}_{{2}}={h} f{{\left({x}+\frac{h}{{2}},{y}+\frac{{F}_{{1}}}{{2}}\right)}}$F2​=hf(x+2h​,y+2F1​​) $\displaystyle={0.1}{\left(\frac{{{5}{\left({0.05}\right)}^{2}-{0.98160602794}}}{{e}^{{{0.05}+{0.98160602794}}}}\right)}$=0.1(e0.05+0.981606027945(0.05)2−0.98160602794​) $\displaystyle=-{0.03454223937}$=−0.03454223937
For $\displaystyle{F}_{{3}}$F3​, we need to know:

$\displaystyle{y}+\frac{{F}_{{2}}}{{2}}$y+2F2​​ $\displaystyle={1}+\frac{{-{0.03454223937}}}{{2}}$=1+2−0.03454223937​ $\displaystyle={0.98272888031}$=0.98272888031

So
$\displaystyle{F}_{{3}}={h} f{{\left({x}+\frac{h}{{2}},{y}+\frac{{F}_{{2}}}{{2}}\right)}}$F3​=hf(x+2h​,y+2F2​​) $\displaystyle={0.1}{\left(\frac{{{5}{\left({0.05}\right)}^{2}-{0.98272888031}}}{{e}^{{{0.05}+{0.98272888031}}}}\right)}$=0.1(e0.05+0.982728880315(0.05)2−0.98272888031​) $\displaystyle=-{0.03454345267}$=−0.03454345267
For $\displaystyle{F}_{{4}}$F4​, we need to know:

$\displaystyle{y}+{F}_{{3}}$y+F3​ $\displaystyle={1}-{0.03454345267}$=1−0.03454345267 $\displaystyle={0.96545654732}$=0.96545654732

So
$\displaystyle{F}_{{4}}={h} f{{\left({x}+{h},{y}+{F}_{{3}}\right)}}$F4​=hf(x+h,y+F3​) $\displaystyle={0.1}{\left(\frac{{{5}{\left({0.1}\right)}^{2}-{0.96545654732}}}{{e}^{{{0.1}+{0.96545654732}}}}\right)}$=0.1(e0.1+0.965456547325(0.1)2−0.96545654732​) $\displaystyle=-{0.03154393258}$=−0.03154393258

Step 2

Next, we take those 4 values and substitute them into the Runge-Kutta RK4 formula:
$\displaystyle{y}{\left({x}+{h}\right)}$y(x+h) $\displaystyle={y}{\left({x}\right)}+\frac{1}{{6}}{\left({F}_{{1}}+{2}{F}_{{2}}+{2}{F}_{{3}}+{F}_{{4}}\right)}$=y(x)+61​(F1​+2F2​+2F3​+F4​)

$\displaystyle={1}+\frac{1}{{6}}{\left(-{0.03678794411}\right.}$=1+61​(−0.03678794411 $\displaystyle-\ {2}\times{0.03454223937}$− 2×0.03454223937 $\displaystyle-\ {2}\times{0.03454345267}$− 2×0.03454345267 $\displaystyle{\left.-\ {0.03154393258}\right)}$− 0.03154393258)

$\displaystyle={0.9655827899}$=0.9655827899
Using this new $\displaystyle{y}$y-value, we would start again, finding the new $\displaystyle{F}_{{1}}$F1​, $\displaystyle{F}_{{2}}$F2​, $\displaystyle{F}_{{3}}$F3​ and $\displaystyle{F}_{{4}}$F4​, and substitute into the Runge-Kutta formula.
We continue with this process, and construct the following table. (I used a spreadsheet to obtain the table. Using calculator is very tedious, and error-prone.)
The table is super wide, so I have put it in the following link:

View table

$\displaystyle{x}$x	$\displaystyle{y}$y	$\displaystyle{F}_{{1}}={h}\frac{{\left.{d}{y}\right.}}{{\left.{d}{x}\right.}}$F1​=hdxdy​	$\displaystyle{x}+\frac{h}{{2}}$x+2h​	$\displaystyle{y}+\frac{{F}_{{1}}}{{2}}$y+2F1​​	$\displaystyle{F}_{{2}}$F2​	$\displaystyle{y}+\frac{{F}_{{2}}}{{2}}$y+2F2​​	$\displaystyle{F}_{{3}}$F3​	$\displaystyle{x}+{h}$x+h	$\displaystyle{y}+{F}_{{3}}$y+F3​	$\displaystyle{F}_{{4}}$F4​
0	1	−0.0367879441	0.05	0.9816060279	−0.0345422394	0.9827288803	−0.0345434527	0.1	0.9654565473	−0.0315439326
0.1	0.9655827899	−0.0315443	0.15	0.9498106398	−0.0278769283	0.9516443257	−0.0278867954	0.2	0.9376959945	−0.023647342
0.2	0.937796275	−0.023648185	0.25	0.9259721824	−0.0189267761	0.9283328869	−0.0189548088	0.3	0.9188414662	−0.0138576597
0.3	0.9189181059	−0.0138588628	0.35	0.9119886745	−0.0084782396	0.9146789861	−0.0085314167	0.4	0.9103866892	−0.0029773028
0.4	0.9104421929	−0.0029786344	0.45	0.9089528756	0.0026604329	0.9117724093	0.002580704	0.5	0.9130228969	0.0082022376
0.5	0.913059839	0.0082010354	0.55	0.9171603567	0.013727301	0.9199234895	0.0136258867	0.6	0.9266857257	0.018973147
0.6	0.9267065986	0.0189722976	0.65	0.9361927474	0.0240794197	0.9387463085	0.0239658709	0.7	0.9506724696	0.0287752146
0.7	0.9506796142	0.0287748718	0.75	0.9650670501	0.0332448616	0.967302045	0.0331305132	0.8	0.9838101274	0.0372312889
0.8	0.9838057659	0.0372315245	0.85	1.0024215282	0.0409408747	1.0042762033	0.0408359751	0.9	1.024641741	0.0441484563
0.9	1.024628046	0.0441492608	0.95	1.0467026764	0.0470593807	1.0481577363	0.0469712279	1	1.0715992739	0.0494916177
1	1.0715783953

I haven't included any values after $\displaystyle{y}$y in the bottom row as we won't be using them.

Easy to understand math videos:
MathTutorDVD.com

Here is the graph of the solutions we found, from $\displaystyle{x}={0}$x=0 to $\displaystyle{x}={1}$x=1.

For interest, I extended the result up to $\displaystyle{x}={10}$x=10, and here is the resulting graph:

Exercise

Solve the following using RK4 (Runge-Kutta Method of Order 4) for $\displaystyle{0}\le{x}\le{2}$0≤x≤2. Use a step size of $\displaystyle{h}={0.2}$h=0.2:

$\displaystyle\frac{{\left.{d}{y}\right.}}{{\left.{d}{x}\right.}}={\left({x}+{y}\right)} \sin{{x}}{y}$dxdy​=(x+y)sinxy
$\displaystyle{y}{\left({0}\right)}={5}$y(0)=5

Show answer

Here's the table of values we get. Once again, it's a very wide table so I've put it separately here:

View table

Here is the graph of the solutions we found, from $\displaystyle{x}={0}$x=0 to $\displaystyle{x}={2}$x=2.

For interest, I extended the result up to $\displaystyle{x}={6}$x=6, and here is the resulting graph:

We observe the graph is not very smooth. If we use a smaller $\displaystyle{h}$h value, the curve will generally be smoother.
In fact, this curve is asymptotic to the $\displaystyle{x}$x-axis (it smoothly gets closer to the axis as $\displaystyle{x}$x gets larger). The above graph shows what happens when our intervals are too coarse. (Those wiggles after around $\displaystyle{x}>{4.5}$x>4.5 should not be there.)
Here is the solution graph again, but this time I've used $\displaystyle{h}={0.1}$h=0.1. It's better, but still has a "wiggle" near $\displaystyle{x}={5}$x=5 that should not be there.

If I took even smaller values of $\displaystyle{h}$h, I'd get a smoother curve. However, that's only up to a point, because rounding errors become significant eventually. Also, computing time goes up for little added benefit.

Improvements to Runge-Kutta

As you can see from the above example, there are points in the curve where the $\displaystyle{y}$y values change relatively quickly (between $\displaystyle{0}$0 and $\displaystyle{1}$1) and other places where the curve is more nearly linear (from $\displaystyle{1}$1 to $\displaystyle{2}$2). Also, we have strange behavior near $\displaystyle{x}={5}$x=5.
In practice, when writing a computer program to perform Runge-Kutta, we allow for variable $\displaystyle{h}$h values - quite small when the curve is changing quickly, and larger $\displaystyle{h}$h values when the curve is relatively smooth.
Mathematics computer algebra systems (like Mathcad, Mathematica and Maple) include routines that calculate RK4 for us, so we just need to provide the function and the interval of interest.

Caution

Always be wary of your answers! Numerical solutions are only ever approximations, and under certain conditions, you can get chaotic results.

IntMath forum

Latest Differential Equations forum posts:

Got questions about this chapter?
Differential equation - has y^2 by Aage [Pending...]
Differential equation by Struggling [Pending...]
dy/dx = xe^(y-2x), form differntial eqaution by grabbitmedia [Solved!]
ODE seperable method by Ahmed [Pending...]
solve the rlc transients AC circuits by Kingston [Solved!]

top

11. Euler's Method - a numerical solution for Differential Equations