https://docs.microsoft.com/en-us/windows/application-management/per-user-services-in-windows
Browse to System\CurrentControlSet\Services\PimIndexMaintenanceSvc. In the list of values, highlight Start and click Select.
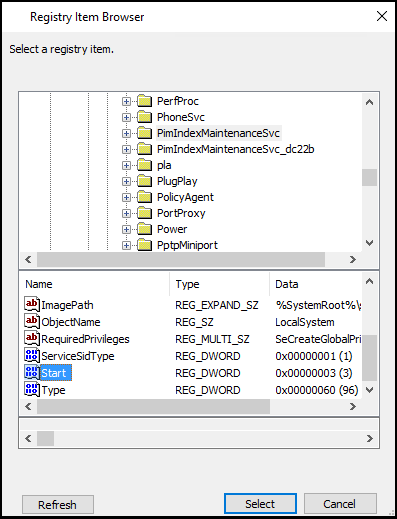
https://docs.microsoft.com/en-us/windows/application-management/per-user-services-in-windows
Browse to System\CurrentControlSet\Services\PimIndexMaintenanceSvc. In the list of values, highlight Start and click Select.

https://endurtech.com/should-i-disable-windows-10-onesyncsvc-service/
The OneSyncSvc synchronizes your Microsoft Account, OneDrive, Windows Mail, Contacts, Calendar and various other Apps. Your Mail App and other Apps and services, which are dependent upon this functionality, will not work properly when this service is disabled or not running.
Since I don’t personally use any of these services or its related Apps I decided to disable it. To my bliss, browsing my Workgroup network with Windows Explorer is near instantaneous by comparison. In short, there are no more delays in opening networked folders.
Again, assuming you don’t use or need any of the above related services or Apps and want to browse your networked computers faster give disabling the OneSyncSvc service a try. To disable OneSyncSvc click “Start” and type “regedit” then press “Enter” on your keyboard. Copy and paste the below address into the address bar at the top:
HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Services\OneSyncSvc
Locate and set the “Start” DWORD from the default value of “2” to “4“. A restart would be required to implement this change.
You would then want to “Favorite” this location within your Registry Editor in case you change your mind or run into issues. Then simply revert the Start DWORD back to “2” to enable the OneSyncSvc service and all its related functionality. Once again, a restart would be required to implement this change.

I hope this article has helped increase the speed with which you browse your networked environment. I welcome your thoughts, questions or suggestions regarding this article.
Again, if you use any of the above mentioned services you would not want to disable the OneSyncSvc service.
You may support my work and future improvements by sending me a tip using your Brave browser or by sending me a one time donation using your credit card.
Let me know if you found any errors within my article or if I may further assist you by answering any additional questions you may have.
https://superuser.com/questions/1334438/how-to-disable-onesyncsvc-c523d-on-win10
The easy way to disable the OneSync service (and it's mirror) is to use the Registry.
regedit and press Enter.Computer\HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Services\OneSyncSvc_c523d. N.B. MS may change the suffix for that key, so look for OneSyncSvc_, knowing the last few characters may differ.Start to 4, which means "disabled". N.B. if you are not an Administrator, or if the key is owned by TrustedInstaller, you may need to change owner and permissions on the key OneSyncSvc_c523d and its subkeys.Buen Libro de Estadistica Descripotiva con ejemplos prácticos
https://drive.google.com/file/d/1s4qC_dgQGjQiBGkljcns15sZvp2gJsYU/view?usp=sharing
https://silo.tips/download/instituto-superior-tecnologico-norbert-wiener-19

INSTITUTO SUPERIOR TECNOLÓGICO NORBERT WIENER
 |
Manual del
Alumno
ASIGNATURA: Estadística I
Los hombres dudan muchas veces antes de dar el primer paso,
porque piensan que no podrán alcanzar la meta que se han propuesto. Esta
actitud es el principal obstáculo que se opone a su progreso, y que cada uno de
nosotros con un pequeño esfuerzo de voluntad puede vencer.
Mahatma Gandhi
![]()
ESTADISTICA I
Índice General
Pag N° 1. Estadística General................................................................................................... 5
2.
Estadística Descriptiva........................................................ 7
3.
Las Variables Estadísticas................................................. 10
4.
La Organización de los Datos…........................................ 11
5. Práctica Calificada……..........................................................
6.
Presentación de los Datos.................................................. 24
7.
Estadígrafos de Tendencia Central.................................... 25
8.
Estadígrafos de Tendencia Central.................................... 29
9.
Estadígrafos de Tendencia No Central.............................. 35
11
Estadígrafos de Dispersión…............................................. 41
![]() 12. Distribución
Bidimensional............................................... 34
12. Distribución
Bidimensional............................................... 34
14. Regresión Lineal…............................................................ 45
15. Regresión Lineal - Análisis de Correlación....................... 49
16. Análisis de Regresión Lineal............................................. 65
17. Números Indices................................................................ 75
Problemas resueltos…............................................................ 83
10.
Problemas
propuestos....................................................... 90
![]()
SESION #1
CAPITULO I – ESTADISTICA
GENERAL
DEFINICION
Y CLASIFICACION DE LA ESTADISITICA
ESTADISTICA: Es una ciencia aplicada a cualquier tema
del saber humano y se encarga de
recopilar, ordenar, clasificar y presentar una información llamada Muestra, con
el fin de inferir acerca del comportamiento de una población.
La Estadística se clasifica en:
1.
Estadística Descriptiva; es la que se encarga de recopilar, ordenar,
clasificar y presenta una información, llamada muestra aleatoria.
2.
Estadística Inferencial; es la parte de la Estadística que se encarga de
inferir sobre el comportamiento de una población a partir de una muestra, bajo un margen de error o incertidumbre
que es cuantificado por la teoría de probabilidades.
CONCEPTOS FUNDAMENTALES EN
ESTADISTICA
POBLACION: Es
un conjunto de observaciones que tienen una característica en común la cual se
desea estudiar, la población representa la totalidad de elementos de un
determinado estudio y puede ser finita o infinita.
Ejemplos:
1.
Habitantes de Lima (aptos para el sufragio). Población Infinita
![]()
2.
Alumnos de WIENER (altura en
mts.) Población Finita
Una población si es infinita no se puede estudiar
en forma completa; aún si es finita es muy engorroso estudiarla en forma
completa por que involucra pérdida de tiempo, dinero, etc., por esta razón nos
basamos en una muestra aleatoria.
MUESTRA
Es un subconjunto de la población y para que la
muestra sea representativa debe ser aleatoria o no sesgada.
Una
muestra es aleatoria cuando cada elemento de la población tiene la misma
posibilidad de ser seleccionado en la muestra.
La
demostraremos por: n= tamaño de la
muestra ó número total de observaciones en la muestra.
Ejemplos:
1. Encuesta a 900 personas
de Lima aptos para el sufragio. n = 900
2. Altura (mts) de 45
alumnos de WIENER
n = 45.
PARAMETRO
Número
que representa a la población. Este valor generalmente es estimado a partir de
una muestra, porque para que sea calculado exactamente se requiere de la
información completa de una población lo cual es muy difícil (los procesos de
estimación de parámetros será tema de estudio en Estadística Inferencial).
ESTADIGRAFO
Llamado
también estadístico o estimador. Número que representa a la muestra y que puede
ser calculado teniendo la información de una muestra. Los Estadígrafos se
dividen en:
![]()
1. Estadígrafos de Posición o Tendencia Central: Son aquellos números que tienden al centro de las observaciones.
2. Es tadígrafos de Dispersión: Son aquellos números que cuantifican la
variabilidad de las observaciones de una muestra.
DATO:
Es la recopilación
o anotación de cada característica de las observaciones de una muestra.
Ejemplo:
Altura (mts) de n=5 alumnos de WIENER: 1.65, 1.59, 1.68, 1.63,
1.69.
SESION # 2
CAPITULO
II – ESTADISTICA DESCRIPTIVA
La Estadística Descriptiva, se encarga de recopilar
la información de una muestra aleatoria, esta información
tiene que ser ordenada para una buena presentación; Esta ordenación se basa en
las llamadas Tablas de Frecuencias y
también en los Gráficos Estadísticos.
RECOPILACION DE DATOS
Es el momento en el cual el investigador se pone en
contacto con los objetos o elementos sometidos a estudio, con el propósito de
obtener datos o respuestas de las variables consideradas; a partir de estos
![]()
datos o respuestas se calculan los Estadígrafos o
indicadores estadísticos.
FUENTES DE DATOS
La fuente de datos, es el lugar, la institución,
las personas o elementos donde están o que poseen los datos que se necesitan para
cada uno de las variables o aspectos de la investigación o estudio.
En general, se puede
disponer de cinco tipos de fuentes de datos:
1.
Las Oficinas de Estadística.- Como instituciones
responsables de recopilar, procesar y publicar las estadísticas sociales o
nacionales.
2.
Archivos o Registros Administrativos.- Como el Registro Civil,
Electoral, Escalafón o Personal, Padrón de Contribuyentes, etc.. Estos
registros no tienen fines Estadísticos, su función es de tipo legal y
administrativo, sin embargo pueden utilizarse como fuentes de datos estadísticos.
3.
Documentos.- Boletines, e informes estadísticos que son las publicaciones o estudios que preparan
los organismos especializados.
4.
Encuestas y Censos.- Son fuentes directas y especiales, que se
construyen en un momento determinado, recopilando datos de una parte o de la
totalidad de una población.
5.
Los Elementos o Sujetos.- Son aquellos que están sometidos a un estudio,
pueden ser personas, instituciones, animales u objetos.
![]()
TECNICAS DE
RECOPILACION O RECOLECCION DE DATOS
Es el conjunto de métodos y procedimientos que se
llevan a cabo para recolectar los datos.
Las más frecuentes técnicas utilizadas son:
1.
La Observación.- Es la acción de mirar de mirar en forma sistemática y
profunda, con el interés de descubrir la importancia de aquello que se observa.
2.
La Técnica Documental.- Es aquella que busca datos a través de
documentos, fuentes escritas o gráficas de todo tipo. Ejm.: Libros, Informes,
Autobiografías, fotografías, planos, videos,
etc.
3.
La Entrevista.- Es la interrelación o diálogo entre personas, donde una
de ellas se llama Entrevistador o Encuestador quien solicita a otra persona
llamada Entrevistado o Encuestado le proporcione algunos datos o información.
4.
El Cuestionario.- Es un instrumento constituido por un conjunto de
preguntas sistemáticamente elaboradas, que se formulan al Entrevistado o
Encuestado, con el propósito de obtener los datos de las variables consideradas
en el estudio. El Cuestionario se desarrolla en el Formulario o Cédula, en
donde las preguntas están debidamente organizadas.
5.
La Encuesta.- Es la técnica por la cual se obtiene la información tal
como se necesita, preparada exprofesamente y con objetivo estadístico. Permite
observar y registrar características en las unidades de análisis de una determinada población o muestra,
![]()
delimitada en el tiempo y en el espacio. El
Entrevistado da respuesta a las preguntas en el formulario o Cédula..
SESION # 3
CAPITULO
III – LAS VARIABLES ESTADISTICAS
LA VARIABLE:
Es la representación simbólica de los datos.
Ejemplo:
Sea X: altura de 5 alumnos de WIENER Donde: Xi,
i= 1 a 5 X1= 1.65 mts., X4 = 1.63 mts.
Las variables se
clasifican en:
I.
Variable Cualitativa: Es aquella variable que representa a datos que
indican cualidades, características, propiedades, etc., no son numéricas (no medibles).
Ejemplos:
X = Control de calidad de productos de una industria. Bueno, Malo, Regular, Muy Bueno.
Y = Estado Civil de una muestra de 200
personas. Soltero, Casado, Viudo, Divorciado.
II.
Variable Cuantitativa: Es aquella variable que representa a datos que
indican valores numéricos (son medibles), y se clasifican en:
![]()
Variable Discreta: Es aquella que representa a datos numéricos que no
se pueden fraccionar, sirven para contar o enumerar (pertenecen a los reales).
Variable Continua: Es aquella variable que representa a datos
que pueden ser fraccionados (pertenecen a los reales).
Ejemplo: El Peso (Kg.) de 6 personas. 65, 56,
59, 70, 63.
La variable continua es la que más utilizamos,
especialmente para los estudios correspondientes en Ingeniería (Volumen,
Temperatura, Pesos, Mediciones, etc.).
SESION # 4
CAPITULO
IV – LA ORGANIZACIÓN DE LOS DATOS
Distribución o Tablas de Frecuencias: Es la condensación, simplificación, ordenación, del
conjunto de observaciones que forman la muestra; la característica principal es
no perder ningún dato de la muestra.
También se puede decir que la Distribución de Frecuencia es la
representación estructurada, en forma de tabla, de toda la información que se
ha recogido sobre la variable que se estudia.
![]() Categorías
o Clases.- Son los datos que están agrupados por sus características comunes.
Categorías
o Clases.- Son los datos que están agrupados por sus características comunes.
![]()
Frecuencia de Clases.- Es el número o cantidad de datos que componen
una Categoría o Clase. Las Frecuencias se clasifican en :
1.
Frecuencia Absoluta (Simple).- Representa a
la cantidad de datos de cada Clase.
2.
Frecuencia Absoluta Acumulada.- Representa a
la suma en forma acumulativa de Clase en
Clase de sus respectivas Frecuencias Absolutas.
3.
Frecuencia Relativa (Simple) .- Es el % que
representa a la cantidad de datos de una Clase con respecto al total de datos.
4.
Frecuencia Relativa Acumulada.- Representa a
la suma en forma acumulativa de Clase en Clase de sus respectivas Frecuencias
Relativas.
Veamos un ejemplo
(4.1) :
Medimos la altura de los niños de una clase y
obtenemos los siguientes resultados (cm):
|
Alumno |
Estatura |
Alumno |
Estatura |
Alumno |
Estatura |
|
|
|
|
|
|
|
|
Alumno 1 |
1,25 |
Alumno 11 |
1,23 |
Alumno 21 |
1,21 |
|
Alumno 2 |
1,28 |
Alumno 12 |
1,26 |
Alumno 22 |
1,29 |
|
Alumno 3 |
1,27 |
Alumno 13 |
1,30 |
Alumno 23 |
1,26 |
|
Alumno 4 |
1,21 |
Alumno 14 |
1,21 |
Alumno 24 |
1,22 |
|
Alumno 5 |
1,22 |
Alumno 15 |
1,28 |
Alumno 25 |
1,28 |
|
Alumno 6 |
1,29 |
Alumno 16 |
1,30 |
Alumno 26 |
1,27 |
|
Alumno 7 |
1,30 |
Alumno 17 |
1,22 |
Alumno 27 |
1,26 |
|
Alumno 8 |
1,24 |
Alumno 18 |
1,25 |
Alumno 28 |
1,23 |
|
Alumno 9 |
1,27 |
Alumno 19 |
1,20 |
Alumno 29 |
1,22 |
|
Alumno 10 |
1,29 |
Alumno 20 |
1,28 |
Alumno 30 |
1,21 |
Si presentamos esta información estructurada
obtendríamos la siguiente Tabla de Frecuencias:
![]()
|
Variable |
Frecuencias
Absolutas |
Frecuencias
Relativas |
||
|
(Valor) |
Simple |
Acumulada |
Simple |
Acumulada |
|
|
|
|
|
|
|
1,20 |
1 |
1 |
3,3% |
3,3% |
|
1,21 |
4 |
5 |
13,3% |
16,6% |
|
1,22 |
4 |
9 |
13,3% |
30,0% |
|
1,23 |
2 |
11 |
6,6% |
36,6% |
|
1,24 |
1 |
12 |
3,3% |
40,0% |
|
1,25 |
2 |
14 |
6,6% |
46,6% |
|
1,26 |
3 |
17 |
10,0% |
56,6% |
|
1,27 |
3 |
20 |
10,0% |
66,6% |
|
1,28 |
4 |
24 |
13,3% |
80,0% |
|
1,29 |
3 |
27 |
10,0% |
90,0% |
|
1,30 |
3 |
30 |
10,0% |
100,0% |
Si los valores que toma la variable son muy
diversos y cada uno de ellos se repite muy pocas veces, entonces conviene
agruparlos por intervalos, ya que de otra manera obtendríamos una tabla de
frecuencia muy extensa que aportaría muy poco valor a efectos de síntesis.
Según los tipos de variables y formas de la tabla
de frecuencias, tendremos las siguientes Tablas de frecuencias
1ER. CASO:
Tablas de Frecuencias para la variable Cualitativa:
En
este caso como la variable cualitativa indica cualidades, propiedades, etc., y
no son medibles; entonces se agrupa de acuerdo a cada categoría que se
diferencia en la variable cualitativa. (Sin un orden establecido).
Ejemplo: (4.2).
Se tiene la
siguiente información que representa el Estado Civil de 50 personas encuestadas
(edad; 20-30 años).
|
Estado Civil |
No. de personas |
% |
|
Soltero |
25 |
50% |
|
Casado |
10 |
20% |
|
Viudo |
1 |
2% |
|
Divorciado |
6 |
12% |
|
Conviviente |
8 |
16% |

![]() Los gráficos que se
presentan en este caso son los siguientes: 1). Diagrama de barra:
Los gráficos que se
presentan en este caso son los siguientes: 1). Diagrama de barra:
2. Gráfico por Sectores Circulares.
 |
2DO. CASO: Tabla de frecuencia para la variable discreta y n
< 30 :
En
este caso la variable es discreta y la muestra pequeña, además hay que
considerar que no haya muchos datos diferentes. La Tabla de frecuencias es por
CLASES, donde cada clase representa el valor numérico de la variable.
![]()
La tdf es de la sgte. forma general:
|
Clase Xi |
Fi |
Fi |
hi |
Hi |
|
x1 |
f1 |
F1 |
h1 |
H1 |
|
x2 |
f2 |
F2 |
h2 |
H2 |
|
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
|
Xm |
Fm |
Fm=n |
hm |
.Hm=1 |
Donde:
n = numero de clases o intervalos de clase.
fi = frecuencia absoluta: es el número de
observaciones que hay en cada clase o intervalo de clase. Además:
fi+f2+f3+.... + fm =n
 |
Fi = frecuencia absoluta acumulada: es
el numero de observaciones acumuladas hasta la clase i, es decir:
F1=f1 F2=f1+f2
.
.
![]()
Fm=f1+f2+f3...+fm =
hi = frecuencia relativa: representa la
relación que existe entre la frecuencia absoluta y el número total de
observaciones:
 |
Generalmente la
frecuencia relativa se expresa en forma porcentual: hi % = 100%.
Hi = frecuencia relativa acumulada: frecuencias relativas acumuladas hasta la clase i.
Hi=h1 H2=h1+h2
.
. Hm=h1+h2+....hm=1
 También :
También :
Se expresa en forma
porcentual. Hi x 100%
Ejemplo:
![]()
Los siguientes datos representan el numero de
defectos en 15
diskettes: 5, 10, 5, 11,6,6,3,3,3,5,5,5,10,6,3.
Agrupar en tabla de
frecuencias:
Solución:
Como la muestra es pequeña y la variable representa
a datos discretos, entonces agrupamos en clases:
|
No de Defectos Xi |
No. diskettes fi |
Fi |
hi% |
Hi% |
|
3 |
4 |
4 |
26.7 |
23.7 |
|
5 |
5 |
9 |
33.3 |
60.0 |
|
6 |
3 |
12 |
20.0 |
80.0 |
|
10 |
2 |
14 |
13.3 |
93.3 |
|
11 |
1 |
15 |
6.7 |
100.0 |
Los gráficos que se presentan en este 2do. Caso
son:
![]() 1. Histograma de
frecuencias: En el sistema de coordenadas rectangulares comparamos
Xi vs. fi (o hi%).
1. Histograma de
frecuencias: En el sistema de coordenadas rectangulares comparamos
Xi vs. fi (o hi%).

![]() 3ER. CASO: Tabla de frecuencias por intervalos de clase:
3ER. CASO: Tabla de frecuencias por intervalos de clase:
En este caso generalmente la variable es continua,
también puede ser usado para la variable discreta siendo la muestra grande (generalmente n >= 30).
La tdf tiene la siguiente forma:
|
Intervalos (Li - Ls) |
Xi |
Fi |
Fi |
hi |
Hi |
|
[X’o - X’1> |
X1 |
f1 |
F1 |
h1 |
H1 |
|
[X’1 - X’2> |
X2 |
f2 |
F2 |
h2 |
H2 |
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
|
[X’m-1- X’m] |
Xm |
Fm |
Fm |
hm |
Hm |
Donde:
![]()
X i= marca de clase o
punto medio de cada intervalo de clase, se obtiene mediante la semisuma de los
limites de cada intervalo.
X i = Ls
+ Li
2
fi , Fi, hi, Hi ; representan las frecuencias definidas en el
caso anterior.
Procedimiento
para construir una tdf por intervalos de clase:
1er. Paso:
Calcular el número de intervalos de clase (K):
Para calcular el valor de K, tenemos dos criterios:
a)
Criterio personal; de acuerdo a la experiencia del investigador se puede
asumir un valor de m para un tamaño de muestra
determinado.
b)
Mediante la Regla de Sturges:
K =1 +3.3 log. n
2do. Paso:
Calcular la amplitud o tamaño del intervalo de
clase:(A)
Para calcular la
amplitud del intervalo (A) nos basaremos en la siguiente expresión:
![]()
A = Rango de la
muestra
K
donde: Rango de la muestra = Valor Mayor – Valor
Menor
Con este procedimiento calculamos una amplitud que
será constante para cada intervalo, y lo mismo ocurrirá entre cada marca de
clase.
Los intervalos serán de la forma: [Li
Ls], pudiendo ser considerado cerrado en el último intervalo.
La amplitud A es
preferible que sea redondeada considerando la misma cantidad de decimales que
tengan los dato de la muestra.
3er. Paso: Tabulaciones
Tabular y presentar los datos agrupados en la
tdf.,
Ejemplos: (2.3)
Los siguientes datos
representan el peso (gr.) de 35 sobrecitos
de unas sustancias: 68, 73, 61, 46, 49,
96, 68, 90, 97, 53, 75, 93, 72, 60,
71, 75, 74, 75, 71, 77, 83, 68, 85, 76, 88, 59, 78, 62, 55, 48, 43, 47,
60, 84, 80. Agrupar en tdf. Solución:
1) Calculamos K = 1 +3,3 Log
35 = 6.095 = 6
2)
Calcula la amplitud del intervalo A:
![]()
![]() A 97 43 9
A 97 43 9
6
3)
Tabular en
tdf:
|
Peso (grs) |
Xi |
fi |
Fi |
hi% |
Hi% |
|
[43 – 52> |
47.5 |
5 |
5 |
14.3 |
14.3 |
|
[52 – 61> |
56.5 |
5 |
10 |
14.3 |
28.6 |
|
[61 – 70> |
65.5 |
5 |
15 |
14.3 |
42.9 |
|
[70 – 79> |
74.5 |
11 |
26 |
31.4 |
74.3 |
|
[79 – 88> |
83.5 |
4 |
30 |
11.4 |
85.7 |
|
[88 – 97] |
92.5 |
5 |
35 |
14.3 |
100.0 |
Se observa por ejemplo
que: 11 sobrecitos tienen un peso comprendido en el intervalo [70-79> grs. y
representan el 31.4% del total.
También vemos que 15 sobrecitos pesan menos de 70
grs. y representan el 42.9% del total.
![]()
SESION # 5
PRIMERA
PRACTICA CALIFICADA
SESION # 6
PRESENTACION
DE DATOS
LOS GRAFICOS
Los gráficos son representaciones en forma de
figuras geométricas, de superficie o volumen con el objeto de ilustrar los
cambios o dimensión de una variable, para comparar visualmente dos o más
variables similares o relacionadas. Para una rápida comprensión de situaciones
o variaciones en cantidades, es muy útil traducir los números en gráficos o
imágenes. Por su naturaleza, un gráfico no toma en cuenta los detalles y no
tiene la misma precisión que una tabla estadística.
Veamos algunos tipos de Gráficos :
1.
Histograma
de frecuencias: Representa un conjunto de rectángulos levantados desde cada intervalo de
clase hasta la frecuencia correspondiente (absoluta ó relativa).
2.
Polígono
de frecuencias: Consiste en unir los puntos medios ó marcas de clase levantadas hasta
cada frecuencia correspondientes, generalmente para su construcción nos podemos
basar del Histograma de frecuencias.
Propiedad:
Area del Histograma = Area del Polígono de frecuencia.
3.
Ojiva: Se
construye basándose en un diagrama escalonado, es decir considerando las
frecuencias acumuladas (absoluta ó relativa), y uniendo los límites de cada intervalo.
 HISTOGRAMA Y POLIGONO DE FRECUENCIAS
HISTOGRAMA Y POLIGONO DE FRECUENCIAS
 |
SESION # 7
LOS
ESTADIGRAFOS DE TENDENCIA CENTRAL
Se
llaman así, porque tienden a ubicar el centro de las observaciones; Estos
estadígrafos de posición son: media, mediana, moda, media geométrica, media
armónica, etc. Estudiaremos los más importantes:
![]() 1. La Media Aritmética
1. La Media Aritmética
Llamada también promedio, es el estadigrafo de
posición más simple y fácil de calcular, por eso es el más común.
Se calcula teniendo en
cuenta los siguientes casos:
1er. Caso: Datos no agrupados en tablas de frecuencias:
Sean X1, X2........... , Xn variables que representan
los n datos de una
 |
muestra, la media
aritmética se calcula:
2do. Caso: Datos
Agrupados en tabla de frecuencias:
 En este caso se calcula mediante la siguiente fórmula:
En este caso se calcula mediante la siguiente fórmula:
fi
= frec. Absoluta hi = frec. Relativa
.
 O también:
O también:
|
|
![]()
hi = frec. Relativa
PROPIEDADES DE LA MEDIA ARITMETICA
1. La
media de los datos todos iguales a una misma constante es igual a la constante:
Sea K = cte. y
cada Xi = k -----------------
X X (K ) K
2. ![]()
![]() Si a cada dato e le
suma o resta una constante k, la media queda
sumada o restada por dicha constante:
Si a cada dato e le
suma o resta una constante k, la media queda
sumada o restada por dicha constante:
Si Xi = Xi +
K -------------------- X(Y) = X(X+k) =
X (X) + k
3. Si a cada dato se le
multiplica o divide por una constante k, la media queda multiplicada o dividida
por dicha constante.
4. Sí Yi = Xi*
k---------------------------- X(Y)
= X(X* k) = X (X) * k
NOTA. Todas las propiedades cumplen para datos agrupados
y no agrupados
![]()
![]()
![]()
![]() ( Xi X
) 0
( Xi X
) 0
Datos no agrupados
![]()
![]() ( Xi
( Xi
X )* fi 0
5. La suma de las
desviaciones respecto a la media es
igual a cero.
SESION # 8
ESTADIGRAFOS
DE TENDENCIA CENTRAL
2. Media Geométrica: se eleva cada valor al número de veces que se ha
repetido. Se multiplican todo estos resultados y al producto final se le
calcula la raíz "n" (siendo "n" el total de datos de la
muestra).
Según el tipo de datos que
se analice será más apropiado utilizar la media aritmética o la media
geométrica.
La media geométrica se suele utilizar en series de
datos como tipos de interés anuales, inflación, etc., donde el valor de cada
año tiene un efecto multiplicador
sobre el de los años anteriores. En todo caso, la media aritmética es la medida
de posición central más utilizada.
Lo más positivo de la media es que en su cálculo se
utilizan todos los valores de la
serie, por lo que no se pierde ninguna información.
Sin embargo, presenta el problema de que su valor
(tanto en el caso de la media aritmética como geométrica) se puede ver muy
influido por valores extremos, que se aparten en exceso del resto de la serie.
Estos valores anómalos podrían condicionar en gran medida el valor de la media,
perdiendo ésta representatividad.
3. La Mediana (Me) :
Es aquel estadígrafo de posición que divide en dos
partes iguales al conjunto de observaciones; es decir la mediana representa el
valor central de una distribución de datos ordenados en forma creciente o
decreciente.
1er. Caso: Datos No agrupados en TDF:
Primero se
ordena los datos en forma creciente o decreciente y luego se tiene en cuenta
sí:
a) n es impar. La mediana es el
valor central.
![]()
 Es el elemento
que ocupa la posición (n+1) /2
Es el elemento
que ocupa la posición (n+1) /2
Ejemplo: Calcular la Me de los siguientes valores:
32, 34, 31, 42, 36, 41,
32, 45, 37, n=9
Ordenando: 31, 32, 32,
34, 34, 36, 37, 41, 42, 45.
Observamos el valor
central:
Me=36 (representa
el 5to. dato)
b) n es par.La mediana es igual al
promedio o la semisuma de los valores centrales.
Ejemplo: la Me de 12,21,16,18,20,19,16,15,16,17.
![]() Ordenando: 12,15,16,16,16,17,18,19,20,21,
Ordenando: 12,15,16,16,16,17,18,19,20,21,
2do. Caso: Datos Agrupados en TD:
![]()
 En este caso la Se me calcula mediante la siguiente fórmula:
En este caso la Se me calcula mediante la siguiente fórmula:
Donde:
Li = limite inferior de
la clase mediana.
Ame := tamaño del intervalo de la clase mediana.
Fme-1 = Frec. Abs. Acumulada anterior a la clase mediana.
fme = Frecuencia
absoluta de la clase mediana.
Clase Mediana: Es aquel intervalo que contiene el valor que ocupa la posición media, es
decir contiene a la mediana. Se calcula mediante:
El primer valor Fi mayor o igual que n/2
4. LA MODA (Mo)
Representa al valor
que más se repite en un conjunto de observaciones:
-
Si la distribución de frecuencias tiene un solo valor máximo, entonces: UNIMODAL.
-
Si la distribución presenta más de un valor máximo: , entonces: POLIMODAL.
-
Si no hay algún valor que se repita con más frecuencia: DISTRIBUCION UNIFORME
1er. Caso: Datos no
agrupadas
Señalar el valor que más se repite.
Ej. 4,5,6,7,4,5,4,6,5,5,4,5,5 Mo = 5 UNIMODAL
Ej. 7,7,6,8,8,6,8,7,7,9,12,11,10,8Mo = 8
BIMODAL
2do. Caso: Datos
Agrupados en Tablas de Frecuencias_
 |
![]()
Donde:
Li = limite
inferior de la clase modal. Amo = Amplitud
de la clase modal.
D1 = Diferencia ente la
Frec. Absoluta de la clase modal menos la frecuencia absoluta anterior.
D2 = Diferencia ente la
Frec. Absoluta de la clase modal
menos la siguiente.
Clase Modal: Representa el intervalo con la mayor
frecuencia absoluta.
Ejemplos. (3.1)
![]()
Calcular la Media
Aritmética, Mediana y Moda de la Tabla de frecuencias del ejemplo (2.3).
![]() gramos
gramos
Para calcular la mediana, la clase mediana es el 4to. intervalo:
 gramos
gramos
Para calcular la Moda,
la clase modal es el 4to. intervalo, por que presenta la mayor frecuencia
absoluta.
D1=11 - 5 = 6
D2=11 – 4 =7
![]() Mo 70
Mo 70
9 * 6
![]()
![]() 6 7
6 7
74.15
Gramos
Nota: La media =mediana = moda, si la
distribución es simétrica.
SESION # 9
![]()
ESTADIGRAFOS DE TENDENCIA NO CENTRAL
Las medidas de Posición o de Tendencia no
centrales permiten conocer otros puntos característicos de la distribución que
no son los valores centrales. Entre otros indicadores, se suelen utilizar una
serie de valores que dividen la muestra en tramos iguales:
Cuartiles: son 3 valores que
distribuyen la serie de datos, ordenada de forma creciente o decreciente, en
cuatro tramos iguales, en los que cada uno de ellos concentra el 25% de los
resultados.
Percentiles: son 99 valores que
distribuyen la serie de datos, ordenada de forma creciente o decreciente, en
cien tramos iguales, en los que cada uno de ellos concentra el 1% de los
resultados.
![]()
aunque haría falta distribuciones con mayor
número de datos.
|
Variable |
Frecuencias
absolutas |
Frecuencias
relativas |
||
|
(Valor) |
Simple |
Acumulada |
Simple |
Acumulada |
|
X |
x |
x |
x |
X |
|
1,20 |
1 |
1 |
3,3% |
3,3% |
|
1,21 |
4 |
5 |
13,3% |
16,6% |
|
1,22 |
4 |
9 |
13,3% |
30,0% |
|
1,23 |
2 |
11 |
6,6% |
36,6% |
|
1,24 |
1 |
12 |
3,3% |
40,0% |
|
1,25 |
2 |
14 |
6,6% |
46,6% |
|
1,26 |
3 |
17 |
10,0% |
56,6% |
|
1,27 |
3 |
20 |
10,0% |
66,6% |
|
1,28 |
4 |
24 |
13,3% |
80,0% |
|
1,29 |
3 |
27 |
10,0% |
90,0% |
|
1,30 |
3 |
30 |
10,0% |
100,0% |
2º
cuartil: es el valor 1,26 cm, ya que entre este valor y el 1º cuartil se situa
otro 25% de la frecuencia.
![]()
Atención: cuando un cuartil
recae en un valor que se ha repetido más de una vez (como ocurre en el ejemplo
en los tres cuartiles) la medida de posición no central sería realmente una de
las repeticiones
Fórmulas para calcular los Cuartiles

![]() Q1 Li
Q1 Li
F 2

![]() Q2 Li
Q2 Li
F 2
Para calcular el Tercer Cuartil
Q3 Li

![]() F 2
F 2
Q1 = Primer Cuartil Q2 = Segundo Cuartil Q3 = Tercer Cuartil
 |
![]()
Li = Límite Real inferior de la Clase que contiene el
Cuartil n = Número de datos
F1 = Frec. Acumulada de la clase anterior a la clase del
Cuartil F2 = Frecuencia absoluta de la Clase del Cuartil
i = Intervalo de Clase
Ejemplo: Calcular el Primer Cuartil de la siguiente
distribución de frecuencias, referente al consumo de energía eléctrica de un
grupo de usuarios
|
Consumo Kw Hora |
Número de Consumidor |
Frecuencia Acumulada |
Límites Reales |
|
05 - 24 |
4 |
4 |
4.5 - 24.5 |
|
25 - 44 |
6 |
10 |
24.5 - 44.5 |
|
45 - 64 |
14 |
24 |
44.5 - 64.5 |
|
65 - 84 |
22 |
46 |
64.5 - 84.5 |
|
85 - 104 |
14 |
60 |
84.5 - 104.5 |
|
105 - 124 |
5 |
65 |
104.5 - 124.5 |
|
125 - 144 |
7 |
72 |
124.5 - 144.5 |
|
145 - 164 |
3 |
75 |
144.5 - 164.5 |
|
|
75 |
|
|
 |
Como cada Cuartil representa el 25%, entonces el Primer
Percerntil será el 25%.
Respuesta.- El 25% de los usuarios
consume 57 KW Hora.
CURSO: ESTADISTICA I
![]()
D = El Decil
Li = Límite Real inferior de la Clase que contiene el
Decil D # = El número de Decil que se quiere
hallar
n = Número de datos
F1 = Frec. Acumulada de la clase anterior a la clase del
Cuartil F2 = Frecuencia absoluta de la Clase del Cuartil
i = Intervalo de Clase
Utilizando el ejemplo: Calcular el Cuarto Decil de
la distribución de frecuencias, referente al consumo de energía eléctrica del
grupo de usuarios
 |
Como cada Decil representa el 10%, entonces el Cuarto
Decil será el 40%..
Respuesta.- El 40% de los usuarios
consume 69.95 KW Hora.
 |
P = El Percentil
Li = Límite Real inferior de la Clase que contiene el Percentil
![]()
P # = El número de Percentil que se quiere hallar n =
Número de datos
F1 = Frec. Acumulada de la clase anterior a la clase del
Percentil F2 = Frecuencia absoluta de la Clase del Percentil
i = Intervalo de Clase
Utilizando el ejemplo: Calcular el
Percentil 79 de la distribución de frecuencias, referente al consumo de energía
eléctrica del grupo de usuarios
 |
Como cada Percentil representa el 1%, entonces el
Percerntil 79 será el 79%..
Respuesta.- El 79% de los usuarios
consume 103.43 KW Hora.
SESION # 10
EXAMEN PARCIAL
SESION # 11
ESTADIGRAFOS
DE DISPERSION O VARIABILIDAD
Son
aquellos números que miden o cuantifican la variabilidad de las observaciones,
con respecto a un estadígrafo posición (generalmente la media aritmética). Los
principales estadígrafos de dispersión son los siguientes:
1. LA VARIANZA:
V (X)
 |

Se
define como el promedio del cuadrado de las desviaciones con respecto a la
media.
![]()
![]() Cuando la varianza es muestral, entonces V(x) se puede denotar como y si la varianza es poblacional, entonces
V(x) se denota como .En este capítulo estudiaremos la varianza
Cuando la varianza es muestral, entonces V(x) se puede denotar como y si la varianza es poblacional, entonces
V(x) se denota como .En este capítulo estudiaremos la varianza
muestral.
La varianza se
calcula, teniendo en cuenta los siguientes casos:
1er. Caso: Datos no agrupados en tablas de frecuencia:
|
|
|
|
Desarrollando esta
sumatoria, obtenemos una forma más simple para calcular la varianza:
 |
|
2do.
Caso: Datos agrupados en tablas de frecuencias:
 O también:
O también:
CURSO: ESTADISTICA I
![]()
Desarrollando esta
sumatoria, obtenemos:
 |
O también:
 |
|
Donde: |
|
|
|
Xi |
= |
marca
de clases. |
|
fi |
= |
frecuencia absoluta |
|
hi |
= |
frecuencia relativa |
Propiedades de la Varianza:
1.
V(X) >= 0 (siempre
la varianza es positiva ó
igual a cero).
|
2, |
V(K) = 0 |
Esto es si cada Xi = k (constante). |
|
3. |
V(X+/- K) = V(X) |
si a cada Xi se le suma (o resta), |
|
|
una constante K |
entonces la varianza no varia. |
![]() 4.
4.
![]() CURSO: ESTADISTICA I
CURSO: ESTADISTICA I
si
a cada dato se multiplica (o por una constante K, entonces la
constante sale elevada cuadrado).
Siendo
a y b constantes, X e Y variables independientes
![]()
5.
2.
DESVIACION
STANDART O TIPICA : S(X)
Se
define como la raíz cuadrada positiva de la varianza, y como la varianza esta
expresada en unidades cuadradas, la desviación standart (que esta expresada en
las mismas unidades de los datos), representa mejor la variabilidad de las
observaciones.
 |
3.
COEFICIENTE DE VARIACION: C.V.
Representa la
relación que existe entre la desviación standart y el promedio de un conjunto
de observaciones. El C.V. como no tiene unidades se debe expresar en porcentaje
y sirve como medios de comparación con otras distribuciones de cualquier tipo
de unidad.
Se calcula:
 |
Donde:
S(x) = desviación típica
X = promedio aritmético ó
Ejemplos:
1.
Los siguiente datos son temperaturas en grados Fahrenheit
415,500,480,490,476,500,432,479,489,497,496,478,453.
Sin ordenar en
tablas de frecuencias:
a) Calcular la varianza.
b)
Si a cada dato se le divide entre 5 y luego se suma
10. Hallar la nueva varianza.
Solución:
a)
Primero tenemos que calcular el promedio para datos
no agrupados:
 °F
°F
Entonces,
calculamos la varianza:
b)
![]() Es decir:
Es decir:
 |
Esto se resuelve
usando propiedades:
2. Dada la siguiente
tabla de frecuencias, que representa el peso (grs), de 34 sobres de cartas:
|
Intervalos |
Xi |
fi |
Fi |
|
[ 7 – 8> |
7.5 |
1 |
1 |
|
[ 8 – 9> |
8.5 |
2 |
3 |
|
[ 9 – 10> |
9.5 |
8 |
11 |
|
[10 – 11> |
10.5 |
11 |
22 |
|
[11 – 12> |
11.5 |
6 |
28 |
|
[12 – 13] |
12.5 |
6 |
34 |
a)
Calcular el peso promedio y la mediana.
b)
Calcular el Coeficiente de Variación (C.V.)
Solución:
a)
Calculando el
promedio:
Calculando
la mediana:
![]() Gramos
Gramos
b)
Para calcular el
C.V. debemos primero calcular la varianza
Calculamos la
desviación standart: S(X)=-1.2708 grs. Entonces:
3. Se tiene dos muestras:
En qué muestra cree
Ud. Que halla menos variabilidad?
![]()
![]()
![]()
Solución:
Primero
hay que tener en cuenta que no se puede comparar las desviaciones standares de
cada nuestra, porque están expresadas en
diferente unidades, pero si podemos compararlas con sus C.V. respectivos:
Entonces,
comprando ambos coeficientes nos damos cuenta que existe menor dispersión en
los datos de la primera muestra.
![]()
SESION # 12
CAPITULO V:
DISTRIBUCION BIDIMENSIONAL
ANALISIS
DE REGRESION Y CORRELACION LINEAL SIMPLE
Los
métodos estadísticos presentados lo hemos referido hasta Ahora a una sola
variable, muchos de los problemas de trabajo estadístico, sin embargo
involucran 2 ó más variables. En algunos casos las variables se estudian
Simultáneamente, para ver la forma en que se encuentran interrelacionadas,
también si se desea estudiar una variable de interés particular. Estos dos
casos de problemas se conocen por lo general con los nombres de correlación y regresión.
Antes
de definir estos casos hablaremos sobre aspectos importantes que involucran 2
variables: Distribución Bidimensional.
5.1. Cálculo de la
Covarianza: S (XY)
La
varianza, es la medida que estudia la dispersión de dos variables, se calcula
teniendo en cuenta:
1er.
Caso: Datos no agrupados en tablas de frecuencia: En este
caso, las variables X é Y se toman en forma simultánea; es decir se considera
no agrupados porque se toman los valores
![]()
como puntos cartesianos (pares de valores). (X1,Y2),
(X2,Y2). (Xm,Ym). Esto es:
|
X |
X1 |
X2 |
X3 |
.......... |
XN |
|
Y |
Y1 |
Y2 |
Y3 |
.......... |
YN |
N: número de
observaciones ó total de pares de valores.
 De cada observación se analiza dos variables Simultáneamente. Las
Covarianza; S (XY) se define:
De cada observación se analiza dos variables Simultáneamente. Las
Covarianza; S (XY) se define:
.............................
( I )
desarrollando la
sumatoria y simplificando:
 |
![]()
Para
calcular la covarianza S(XY), es preferible utilizar la ec. (II). Los promedios
de X y de Y, así como las desviaciones standares S(X) Y S(Y), se calculan
como en los capítulos 3 y 4.
2do. Caso: Datos
Agrupados en tablas de frecuencias:
En
este caso cada variable X e Y, están agrupados en tablas de frecuencias
presentándose lo que se llama: Distribución Bidimensional o Tabla de Doble
Entrada.
En forma tabular:
X : agrupado en K intervalos (y = 1... k)
Y : agrupado
en m intervalos (j = 1.. m).
Donde:
Xi : marca de clase (variable X) Yj : marca
de clase (variable Y)
fij : frecuencia absoluta conjunta,
corresponde al número de observaciones que existe en el I-ésimo intervalo de X con el j-ésimo
intervalo de Y.
Observaciones:
(1)
Según la definición de la covarianza (tanto para
datos agrupados como no agrupados), la covarianza puede ser negativa.
(2)
La covarianza presenta unidades de cada una de las
variables involucradas.
(3)
La covarianza S(XY), también se denota: Cov (X,Y)
![]()
Ejemplos:
(5.1) Dada la
siguiente tabla, que representa la medida (X) en cm. De 8 barretas de metal y
el peso (Y) en libras de cada una de ellas, calcular:
a) S(X) b) S(Y) c) S(XY)
|
X |
1 |
3 |
4 |
6 |
8 |
9 |
11 |
14 |
|
Y |
1 |
2 |
4 |
4 |
5 |
7 |
8 |
9 |
Solución:
Este ejemplo,
corresponde a datos no agrupados en tabla de frecuencias.
a)
![]()
|
S2 (X)
=
b) ![]()
|
S2 (Y)
![]()
(5.2) Dada la
siguiente tabla en el cual se estudia las alturas (pulg) y los pesos (libras)
de 300 estudiantes hombres en una Universidad:
X
: altura (pulgadas).
Y
![]()
![]() : peso (libras).
: peso (libras).
|
Y X |
58-62 |
62-66 |
66-70 |
70-74 |
74-78 |
Total fy |
|
90-110 |
2 |
1 |
|
|
|
3 |
|
100-120 |
7 |
8 |
4 |
2 |
|
21 |
|
130-140 |
5 |
15 |
22 |
7 |
1 |
50 |
|
50-160 |
2 |
12 |
63 |
19 |
5 |
101 |
|
170-180 |
|
7 |
28 |
32 |
12 |
79 |
|
190-200 |
|
2 |
10 |
20 |
7 |
39 |
|
210-220 |
|
|
1 |
4 |
2 |
7 |
|
Total Fx |
16 |
45 |
128 |
84 |
27 |
300 |
Calcular:
![]()
S (X) , S(Y) , S (XY)
Solución:
Como
la tabla es Bidimensional, podemos formar tablas de frecuencias para cada una
de las variables por separado, a este proceso se le conoce como TABLAS
MARGINALES.
Tabla marginal para
x::
|
Intervalos |
Xi |
Fi |
|
58 – 62 |
60 |
16 |
|
62 – 66 |
64 |
45 |
|
66 – 70 |
68 |
128 |
|
70 – 74 |
72 |
84 |
|
74 – 78 |
76 |
27 |
300
Tabla Marginal para Yi:
|
Intervalos |
Yj |
f.j. |
|
90 – 110 |
100 |
3 |
|
110 – 130 |
120 |
21 |
|
130 – 150 |
140 |
50 |
|
150 – 170 |
160 |
101 |
|
170 – 190 |
180 |
79 |
|
190 – 210 |
200 |
39 |
|
210 – 230 |
220 |
7 |
300
La variable X presenta 5 intervalos ( i = 1..... 5)
La variable Y presenta 7 intervalos ( j = 1..... 7)
Calculando:

 |
|
Calculando la Covarianza:
 |
![]()
SESION # 14
REGRESION LINEAL
5.2. Diagrama de
Puntos y Curvas de Ajuste:
Representan
los puntos (X1, Y1), (X2, Y2)..... (XN, YN) en un sistema de coordenadas
rectangulares, donde al sistema de puntos resultantes lo llamaremos Diagrama
de Dispersión o Diagrama de Puntos: Con el diagrama de dispersión es
posible representar una curva que se aproxime a los datos: Curva de
Aproximación.
Entonces, encontrar
ecuaciones de curvas de aproximaciones que se ajusten a los datos, es buscar
una: Curva
de Ajuste.
Tenemos:
a) Conjunto de puntos
que se ajustan a una línea recta (ajuste lineal o relación lineal).
 |
Observamos que el
diagrama de puntos gira alrededor de una recta: Y = a+ bX
![]()
b) Conjunto de puntos o
diagrama de puntos cuya relación no es lineal.
 |
Algunas de las
ecuaciones de curvas de aproximación:
![]()
 Relación
lineal
Relación
lineal
Curva Polinomial
Hipérbola
Entonces,
lo que se desea es encontrar una curva de aproximación que se ajuste mejor a los datos, y así mostrar la
ecuación de la curva respectiva.
El
tipo más sencillo de una curva de aproximación es la línea recta cuya ecuación
puede escribirse: Y = a +b*X
![]()
5.3 Método de mínimos Cuadrados:
![]() De todas las curvas de aproximación a una serie de datos puntuales, la
curva tiene la propiedad de que:
De todas las curvas de aproximación a una serie de datos puntuales, la
curva tiene la propiedad de que:
sea mínimo
Se conoce como la mejor curva de ajuste por
el método de mínimos cuadrados.
Di= desviación de
cada punto con respecto ala línea recta.
Este método
consiste en minimizar la suma de los cuadrados de las desviaciones Di.
Entonces
para ajustar un diagrama de dispersión a la línea recta, utilizaremos este
método de los MINIMOS CUADRADOS. Es decir una recta de aproximación de mínimos
cuadrados del conjunto de puntos (x1, y1), (x2,y2),......,(xn,yn), tiene la
ecuación: Y = a+b*X , donde a y b se determinan mediante el sistema de
ecuaciones normales, son las siguientes:
 |
Donde al desarrollar y despejar a
y b se obtienen:


Otras
ecuaciones más practicas para calcular los valores de a y b de la ecuación
aproximada Y = a +b*X son las siguientes:
 |
|||
Ejemplo:
Sean los valores:
|
x |
3 |
1 |
4 |
6 |
8 |
9 |
11 |
14 |
|
y |
2 |
1 |
4 |
4 |
5 |
7 |
8 |
9 |
a)
Construye el diagrama de puntos
b) Encuentra las
ecuaciones normales
c)
Encuentra la ecuación de la curva de ajuste.
Solución:
a)
Llevando los puntos al sistemas de coordenadas rectangulares.
 |
b) Al observar el
diagrama de puntos, notamos que se aproxima o ajusta a una línea recta, cuya
ecuación es: Y = a+b*X
c)
 |
|||||
 |
|||||
Para encontrar
las ecuaciones normales:
![]()
Entonces las ecuaciones normales son:
40 = 8*a +b* 56
364 = 56*a +b*524
|
Resolviendo el sistema (Método de Mínimos
Cuadrados) a= 6/11 = 0.545 b=7/11=0.636
d) La ecuación
resultante será :
nota : Si la ecuación es Y = a +b*X
entonces b mide la pendiente de la
línea recta.
![]()
SESION # 15
SEGUNDA
PRACTICA CALIFICADA SESION # 16
5.4 Análisis de
correlación lineal simple:
Definición: Estudia
el grado de asociación que existe entre las variables en estudio, el
coeficiente que mide la mutua asociación se denomina: Coeficiente de
Correlación (r).
Las asociaciones que se pueden presentar son:
1)
Correlación o
asociación Positiva (+), es decir a medidas altas de una variable, le
corresponden medidas altas de otra variable, cambios en el mismo sentido
(Relación Directamente Proporcional)
X ![]() entonces Y
entonces Y ![]()
X ![]() entonces Y
entonces Y ![]()
Ejemplo :
altura y peso
2)
Correlación o
Asociación Negativa (-), En este caso, a valores altos de una variable,
corresponden valores bajos de la otra variable y viceversa. (Relación
inversamente proporcional).
3)
Medidas
no Correlaciónales; No existe ninguna asociación entre las variables.
Características de
Coeficiente de Correlación Lineal Simple
1) r se calcula
mediante la siguiente fórmula:
 |
S (XY)
: covarianza de X e Y
S (X) : desviación
standart de X S (Y) : desviación standart de Y
2)
r es un número abstracto (sin
unidades) y oscila entre –1 y 1, es decir:
![]()
3)
- Si
r es positivo (Correlación
Positiva), entonces las dos características tienden a variar en el mismo sentido.
- Si r es negativo (Correlación Negativa), las dos características
tienden a variar en sentido contrario.
4)
Si r=+1 ó r=-1, entonces la asociación es perfecta.
5)
Si r = 0, no existe asociación entre las variables:
6)
La asociación, tiende a ser más estrecha, cuando r:
Ejemplo:
(5.4) Calcula
el coeficiente de correlación, del ejemplo (5.1); donde: S(X) =4.06;
S(Y) =2.65;
S(XY)=10.5
 |
Interpretación.- Existe
una alta asociación entre las variables estudiadas. (5.5) del ejemplo (5.2),
donde: S(X)=3.929 pulgadas S(Y)=24.202
libras,
S(XY)=51.370 pulg/lbs
 |
Interpretación.- Existe asociación entre
las alturas y pesos de los estudiantes de la Universidad dada, esta asociación
es directamente proporcional.
5.4 Análisis de Regresión Lineal Simple:
En las relaciones
entre las variables se pueden presentar los siguientes casos:
i)
![]() X influye en Y : X Y
X influye en Y : X Y
X : variable independiente Y : variable dependiente
Ejemplo:
![]()
|
Edad agilidad mental
ii)
![]() Y influye en X Y X Y: variable independiente
Y influye en X Y X Y: variable independiente
X: Variable dependiente
![]() III) Las dos están
influenciadas entre si: X Y
III) Las dos están
influenciadas entre si: X Y
![]() X Y
X Y
Ejemplo : precio y producción de un articulo.
Definición: La regresión permite estudiar
la dependencia de una característica respecto a la otra, para establecer como
varía el promedio de la primera característica al variar la segunda en una
unidad de su medida.
Se
dice regresión lineal, porque las variaciones de la variable independiente,
pueden provocar variaciones proporcionales en las variables dependientes
(ajuste a la línea recta).
Se
dice que la regresión es simple, si una variable independiente influye sobre
otra variable dependiente.
![]()
Ejemplo:
![]() Proteína de harina volumen de pan
Proteína de harina volumen de pan
![]() Ecuación de
Regresión Lineal Simple.
Ecuación de
Regresión Lineal Simple.
 Es una ecuación para estimar una variable dependiente a partir de la
variable independiente.
Es una ecuación para estimar una variable dependiente a partir de la
variable independiente.
Si X : Variable independiente Y : Variable dependiente
Donde : Y = variable dependiente estimada
: b = coeficiente
de R.L.S.
Características del Coeficiente de R.L.S. (b)
1)
b : indica el número de unidades en que
varía la variable dependiente al variar la independiente en una unidad de su medida.
2)
Si b es positivo los cambios son
directamente proporcionales.
Si b es negativo
entonces los cambios son inversamente proporcional
3)
b : mide la pendiente de la línea de regresión.
4)
b, esta dado en unidades de la variable dependiente.
5)
b y r siempre tienen el mismo signo.
6)
b se calcula:
![]()
![]() Sí Y = f(X), entonces:
Sí Y = f(X), entonces:
 |
Y el valor de la
constante a:
![]() Si X= f (Y) (se
realiza cambio de X por Y y viceversa)
Si X= f (Y) (se
realiza cambio de X por Y y viceversa)
![]()
![]() Línea de Regresión.- consiste en el trazo
o gráfica de la ecuación de regresión lineal simple, es decir el gráfico de los puntos
Línea de Regresión.- consiste en el trazo
o gráfica de la ecuación de regresión lineal simple, es decir el gráfico de los puntos
si la ecuación es:
Regresión
de Y sobre X; o el gráfico de los puntos
(X,Y) si la ecuación es X= a+ bY
: Regresión de X sobre Y.
Ejemplo:
selecciona al azar
cuatro meses de un
año y se registra tanto los ingresos
como los gastos, en miles de dólares, de cierta empresa:
|
Ingreso (miles de dólares) |
10 |
11 |
12 |
13 |
|
Egresos (miles de dólares) |
4 |
5 |
9 |
10 |
I.
Efectuar un estudio de Regresión Lineal Simple,
asumiendo que los egresos están en función de los Ingresos:
1)
Calculando el coeficiente de Regresión b e interpretándolo
2)
Calculando el coeficiente de intersección a
![]()
3)
Encontrando la ecuación de
Regresión Lineal Simple y trazar la
línea de Regresión.
II.
Realiza un análisis de Correlación Lineal Simple, e
interprete el valor de r.
Solución:
I.
Como el egreso está en función de los ingresos:
Egresos: variable
dependiente: Y
Ingresos: variable
independiente: X
1)
Calculando b
Primero calculamos:
Entonces:
![]()
Interpretación.- Por
cada mil dólares adicional en el Ingreso de dicha empresa, habrá un aumento en
el Egreso de 2.2 miles de dólares en promedio.
2)
![]() Para calcular a :
Para calcular a :
3)
Ecuación de Regresión Lineal Simple:
Como Y es variable
dependiente, entonces:
Para el trazo en el
sistema de ejes cartesianos se tendrá que reemplazar en la ecuación de
Regresión, los diferentes valores de X:
Y=-18.30 +2.2. (10) =
3.7
Y=-18.30 +2.2
(11) = 5.9
Y=-18.30
+2.2 (12) = 8.1
Y=-18.30 +2.2 (13)
=10.30
También se puede
estimar nuevos valores de los Egresos (Yi) a partir de un valor Xi.
Ejemplo:
Para un ingreso de
15mil dólares, se espera tener en promedio un Egreso de:
Y
=-18.30 + (2.2) (15) = 14.7 miles de dólares La línea de Regresión: unión de
puntos (Xi,Yi)
II.
|
![]() Análisis de Correlación:
Análisis de Correlación:
![]()
Interpretación.- Existe
una alta asociación entre los ingresos y los egresos, siendo los cambios
directamente proporcionales.
![]()
SESION #17
CAPITULO VI: NUMEROS INDICES
Definición.- Un
número índice es una medida estadística diseñada para mostrar los cambios en
una variable (o en un grupo de variables) con respecto al tiempo, situación
geográfica, renta, profesión, etc.
Aplicaciones:
1. Comparar el costo de
alimentos en otros costos de vida durante un año o período con respecto al año
o período anterior.
2. En negocios y Economía.
Tipos de Indice:
(6.1) Indices Simples: Cambios en un
solo bien determinado
1)
Indices de Precios Relativos.- uno de los
ejemplos más sencillos de número índice es un precio relativo, que representa
la razón del precio de un bien determinado en un período con respecto a otro
período llamado base.
Indice de Precio
Relativo: IPR
Po : precio de un
bien en período base Pn : precio de un bien en período dado
Sí Pa:
precio de un bien en el período a Pb : precio de un bien en el período b
Ejemplo:
(6.1) Supóngase que los precios de consumo de 1 tarro
de leche en junio de 1990 es de 22,000 intis y en junio de 1989 fue de 5,000
intis, tomando 89 como base.
![]() El IPR Simple:
El IPR Simple:
Es
decir: en 1990 el precio de leche fue el 440% del que tenía en el año 89, es
decir se incrementó en un 340%
Observación: IPR Simple es un bien en un
período a (Pa), con respecto al mismo período a (Pa) =1
2)
Indices de Cantidades (o volumen) Relativos.- En lugar de
comparar precios de un bien, se puede también comparar cantidades de un bien
(cantidad de producción, consumo, exportación, etc.) calculemos la cantidad o
volumen relativo (suponiendo que las cantidades dentro de cualquier otro
período son constantes).
Indice de Cantidad
Relativo: IQR
![]()
qn
: cantidad de un bien en el período n
qo : cantidad de un bien en el período base
3)
Valor Relativo.- Si p es precio de un bien durante un período y la
cantidad o volumen producido, vendido, etc., durante ese período.
Valor
total = p * q
Ejemplo:
Si se han vendido
1000 tarros de leche a $0.75 c/u Valor total = 0.75 * 1000 = $ 750
![]()
Si
Po Y qo denotan precio y cantidad de un bien durante un período base y pn y qn
denotan el precio correspondiente durante un período dado, los valores totales
durante estos períodos son Vo y Vn respectivamente y el valor relativo (VR) se define:
(6.2) Indices Compuestos:
En
la práctica, no se esta tan interesada en comparaciones de precios, cantidades
etc., de bienes individualmente considerados, como en comparaciones de grandes
grupos de tales bienes, es decir es preferible considerar un grupo de bienes
para medir los cambios respectivos.
Los
principales Indices compuestos se calculan teniendo en cuenta los siguientes
métodos:
1)
Método de Agregación Simple.- Este método de cálculo de
un índice de precio (o cantidad), expresa el total de los precios (o cantidades) de bienes en el
período dado, como porcentaje del total de los precios (o cantidades de bienes
en el período base.
Tenemos:
Indice de Precios
de Agregación Simple: IPAS
Donde:
![]() Pn = suma total de precios de bienes empleados en el periodo dado. Po =
suma total de precios de bienes empleados en el año base.
Pn = suma total de precios de bienes empleados en el periodo dado. Po =
suma total de precios de bienes empleados en el año base.
Desventaja: No tiene en cuenta la importancia relativa de las cantidades de los diferentes bienes.
2)
método
de Media de Relativo Simple. En
este método existen varias posibilidades dependiendo del procedimiento empleado
para promediar los precios relativos (o cantidades relativas), tal como la
media aritmética, media geométrica, Mediana,
etc.
Tenemos :
Indice de precios
de Media de Relativo Simple: IPMRS (Promedio de los precios relativos de cada
uno de los bienes empleados):
Donde:
![]() (Pn/Po) = suma de
los precios relativos de bienes. N =
número total de bienes empleados.
(Pn/Po) = suma de
los precios relativos de bienes. N =
número total de bienes empleados.
![]()
Método de Agregación Ponderada. Para
salvar algún inconveniente del método de agregación simple, se da un peso al
precio de cada bien mediante un factor adecuado, tomando a menudo una cantidad
o volumen del bien determinado durante el periodo dado, o algún periodo típico
(que puede ser una media de varios años). Tales pesos indican la importancia de
cada bien particular.
Aparecen así, los
tres siguientes índices para precios:
(I). Indice de Precios de Laspeyres (o método del
año base): IPL
Pondera los precios considerando como factor de ponderación a las
cantidades en el periodo base.
Cuando los bienes empleados corresponden a la canasta familiar, el IPL se denomina
índice de Precios del Consumidor o Indice del Costo de Vida, y se utiliza para
medir el nivel de inflación.
(II) Indice de
Precios de Paasche (o método del
año dado): IPP
Pondera los precios de cada bien, considerando como factor de
ponderación a las cantidades del periodo dado.
![]()
(III). Indice Ideal de Fisher
Representa la media geométrica de los índices de Laspeyres y Paasche
(promedio de los índices ponderados).
Ejemplo:
(6.3) La tabla
muestra los precios y cantidades consumidas de cierto país de distintos
productos férreos en los años 79, 86 y 87.
|
Precios ($/Lbs) |
|||
|
Año |
1979 |
1986 |
1987 |
|
Plata |
17.00 |
26.01 |
27.52 |
|
Cobre |
19.36 |
41.88 |
29.99 |
|
Plomo |
15.18 |
15.81 |
14.46 |
|
Staño |
99.32 |
101.26 |
96.17 |
|
Zinc |
12.15 |
13.49 |
11.40 |
|
Cantidad (Mills de bls) |
|||
|
Año |
1979 |
1986 |
1987 |
|
Plata |
1357 |
3707 |
3698 |
|
Cobre |
2144 |
2734 |
2478 |
|
Plomo |
1916 |
2420 |
2276 |
|
Staño |
161 |
202 |
186 |
|
Zinc |
1872 |
2018 |
1424 |
a)
Calcular Indice de Precios de Agregación Simple para
el año 86, considerando como año base 1979
b)
Calcular el IPL para el año 87, con base en el año 79
c) Calcular el IPP para
el año 87, con año 86
Solución
Esto
significa, que los precios del conjunto de productos férreos, en el año 86,
representa el 121.7% de los precios que tenían en el año 79, es decir se
incrementaron en 21%.
Nota:
Las
fórmulas descritas anteriormente para obtener números índice de precios se
modifican fácilmente para obtener números índices de cantidad o volumen, con el
simple intercambio de p y q.
![]()
Ejemplo
: Indice de cantidad de Agregación Simple: IQAS
(6.4) Deflación
Aunque
los ingresos de las personas pueden elevarse teóricamente en un período de dos
años, su ingreso real puede netamente ser inferior, debido al incremento del
costo de vida y por consiguiente su poder de
adquisición.
Ejemplo (5.3)
Si
el ingreso de una persona en 1990 es el 150% de su ingreso en 1989 (es decir a aumentado en 50%)
mientras que el ICV es el 500% del año 89, el salario real de la
persona será en 1990
El
salario real de la persona en 1990 es el 30% del que tenía en 1989, es decir el
poder adquisitivo de esta persona ha disminuido en 70%.
ANEXOS PROBLEMAS RESUELTOS
a)
tablas de frecuencia y Estadigrafos de posición:
1)
|
La siguiente distribución muestra el peso en gramos de 30 paquetes de un
determinado producto:
Se pide completar
la tabla:
Solución
Si la sumatoria de
las hi = 1
Sabemos que : M/2
+ 0.17 +2M +M +0.13 = 1
M/2
+3M = 1-0.30 M/2 +3M = 0.7
![]() 7M = 1.4
7M = 1.4
|
sabemos
que
|
Por lo tanto
Remplazando
valores de hi
|
|
|
|
hi |
hi |
|
M/2 |
0.10 |
|
0.17 |
0.17 |
|
2M |
0.40 |
|
M |
0.20 |
|
0.13 |
0.13 |
Completando el
cuadro:
|
Intervalos |
Xi |
fi |
Fi |
hi |
Hi |
|
[10.5 14.5> |
12.25 |
3 |
3 |
0.10 |
0.10 |
|
[14.5 19.5> |
17 |
5 |
5 |
0.17 |
0.17 |
|
[19.5 24.5> |
22 |
12 |
12 |
0.40 |
0.67 |
|
[24.5 29.5> |
27 |
6 |
6 |
0.20 |
0.87 |
|
[29.5 35> |
32.25 |
4 |
4 |
0.13 |
1.00 |
30 1.00
2)Los siguientes datos son los
puntajes obtenidos por 50 estudiantes en un examen de Estadística I:
|
33, |
35, |
35, |
39, |
41, |
41, |
42, |
45, |
47, |
48, |
|
50, |
52, |
53, |
54, |
55, |
55, |
57, |
59, |
60, |
60, |
|
61, |
64, |
65, |
65, |
65, |
66, |
66, |
66, |
67, |
68, |
|
69, |
71, |
73, |
73, |
74, |
74, |
76, |
77, |
77, |
78, |
|
80, |
81, |
84, |
85, |
85, |
88, |
89, |
91, |
94, |
97. |
Clasificar estos
datos convenientemente en intervalos de clase de igual amplitud y construir los
gráficos respectivos.
Solución
I) Rango
= 97-33 = 64
II) K
= 1+3.32 * log (10) = 1+ 3.22 (1.699) = 6.47
|
![]()
Redondeando
al entero inmediato superior K = 7
(siete intervalos)
III) La amplitud de Clase A
= 64 / 7 = 9.14, aproximando al entero mayor (recuerda que la amplitud debe
tener la característica de los datos)
A = 10
Para facilitar el
conteo de las frecuencias, tomaremos como límite inferior de la primera clase
30.
|
clases |
xi |
fi |
Fi |
hI |
HI |
|
[30, 40> |
35 |
4 |
4 |
0.08 |
0.08 |
|
[40, 50> |
45 |
6 |
10 |
0.12 |
0.20 |
|
[50, 60> |
55 |
8 |
18 |
0.16 |
0.36 |
|
[60,
70 > |
65 |
13 |
31 |
0.26 |
0.62 |
|
[70, 80> |
75 |
9 |
40 |
0.18 |
0.80 |
|
[80, 90> |
85 |
7 |
47 |
0.14 |
0.94 |
|
[90, 100> |
95 |
3 |
50 |
0.06 |
1.00 |
|
TOTAL |
|
50 |
|
1.00 |
|
Nótese que en el
ultimo intervalo el límite superior puede ser abierto ya que sobrepasa al valor
más alto de los datos.
![]() GRAFICOS
GRAFICOS
![]()
2)
El supervisor de una planta de producción desea
comprobar si los pesos netos de las latas de conserva de durazno tienen el peso
reglamentario (18 onzas) para lo cual registra el peso de 36 latas obteniendo
los siguientes datos:
17.0, 17.5,
18.5, 18.1, 17.5,
18.0, 17.5, 17.3,
18.0, 18.0, 18.0,
17.6,
18.2, 17.6, 18.4,
17.7, 17.7, 17.9,
18.3, 17.1, 17.8, 17.3,
18.1,
17.6, 17.7, 18.2, 18.4,
18.0, 18.2, 17.1,
18.6, 18.1, 18.5,
18.4, 17.9, 18.2.
Se pide :
a) Presentar los datos
en una tabla de frecuencia.
b) Determine el peso promedio.
c) Determine el peso
central (la mediana).
d) Determine el peso Modal.
Solución
i) Rango = 18.6 – 17.0 =1.6
ii)
K = 1+ 3.32 * log (36) = 6.17 redondeamos a 6 intervalos
iii)
A = 1.6 / 6 = 0.266 lo aproximamos
a 0.3 (recuerden siempre se redondea
A hacia el mayor respetando la característica de los datos, en este caso con un
digito decimal). A = 0.3
a) La tabla
queda:
![]()
![]()
|
b)
onzas
c)
Para la mediana buscar en Fi aquel que sea igual o
mayor que n/2, es decir
![]()
Fi>= 36/2 =18.
![]() Onzas
Onzas
d) Para calcular la
moda usamos el intervalo de mayor fi
PROBLEMAS PROPUESTOS:
1) La siguiente tabla
muestra las frecuencias relativas de 200 alumnos.
|
EDADES |
16 |
19 |
22 |
25 |
28 |
31 |
|
Hi% |
10 |
15 |
37 |
75 |
85 |
100 |
a) Muestra los límites
de cada intervalo de clase.
b)
Que tanto por ciento de los estudiantes tienen
edades entre 12 y 26 años.
2) Los siguientes datos
son las velocidades en Km./h. De 30 carros que pasaron por un punto de control
de velocidades.
60, 30, 38, 60, 45, 20, 35, 20, 40, 54, 38,
35, 40, 10, 45, 60, 49,
49,
30, 55, 46, 105, 29, 38, 80, 40, 28, 15, 82,
72.
a)
Calcular la media de los datos sin clasificar.
b)
Agrupa estos datos convenientemente.
c) Calcule la media,
mediana y moda.
3)Un grupo de 50
empleados de sistemas de una gran compañía recibe un curso intensivo de
Programación de Ordenadores. De los varios ejercicios distribuidos durante el
curso, se muestra el número de ejercicios completados satisfactoriamente por
los miembros del grupo: 13,
9, 8, 14, 16, 15, 6, 15,
11, 5, 3, 11, 11, 9, 18, 18,
5, 1,15, 12,
16, 12, 14, 9, 6,
10, 5, 12,
17, 11, 12, 13,
8, 19, 12,
11, 18, 15,
13, 9, 10,
9, 10, 7, 21, 16, 12, 9,
2, 13.
a)
Agrupar estas cifras en una tabla de distribución de
frecuencias, usando el método de Sturges.
b)
Calcula la media, mediana y moda.
c)
Estima la desviación típica para datos no agrupados.
4)
Sean los siguientes datos: f1=3, F2=8, F3=18, f5=2, x4=3, K=6,
H4=0.875, A=2, n=24. Completa la tabla de distribución de frecuencias y
calcular la Varianza.
![]() 5)
5)
y dada la siguiente tdf:
|
intervalos |
hi% |
|
[0.5 2.5> |
2% |
|
[2.5 4.5> |
10% |
|
[4.5 6.5> |
h3% |
|
[6.5 8.5> |
16% |
|
[8.5 10.5> |
h5% |
|
[10.5 12.5> |
10% |
|
[12.5 14.5> |
2% |
a) Calcula h3% y h5%
b) Calcula la Varianza.
7) Se tiene una
distribución simétrica de frecuencias con 7
intervalos de igual amplitud A =20 y
considerando los siguientes datos:
X3*f3 = 1260, f2 + f5 = 62, H6% = 96%, f1 =
8, h3% = 21%.
a)
Calcula la media, mediana y moda
b)
Calcula el C.V.
8)
Se conocen los siguientes datos del peso de un grupo
de estudiantes:
![]()
|
= 50
si
se sabe que: h1=h3 y h2=h4
Determina:
a)
La media, mediana y desviación típica.
b) Presenta los datos
en un Histograma y polígono de frecuencias.
![]()
9) Sabiendo que la
tabla de frecuencias, es simétrica, completarla con los datos, dados, si además
se sabe que la mediana es igual a 27.5.
Luego calcula la media, la moda y la desviación estándar.
|
Intervalo |
Xi |
fi |
Fi |
hi |
Hi |
|
L0 L1 |
|
|
|
|
|
|
L1 L2 |
|
|
|
|
|
|
L2 L3 |
|
|
|
0.20 |
|
|
L3 L4 |
|
|
|
|
0.65 |
|
L4 L5 |
|
|
|
|
|
|
L5 50 |
|
|
|
|
0.95 |
|
50 L7 |
|
|
|
|
|
![]() = 60
= 60
10)
Una fabrica tiene dos departamentos uno de
producción y otro de ventas. Las siguientes tablas de frecuencias presentan los
haberes percibidos hasta fines de abril en cada uno de los departamentos.
![]()
|
Haberes
semanales en dólares |
N°de
trabajadores dpto. de
producción |
|
[10 15> |
15 |
|
[15 20> |
25 |
|
[20 25> |
30 |
|
[25 30> |
20 |
|
[30 35> |
5 |
|
[35 40 |
5 |
|
[40 45 |
0 |
|
Total |
100 |
|
Haberes mensuales en dólares |
N° de trabajadores Dpto. de Ventas |
|
[20 60> |
0 |
|
[60 80> |
5 |
|
[80 100> |
5 |
|
[100 120> |
15 |
|
[120 140> |
20 |
|
[140 160> |
5 |
|
total |
50 |
Calcule:
a) El haber promedio
mensual y la desviación típica correspondiente a cada departamento.
b) El haber promedio
mensual y la desviación típica del conjunto de trabajadores de ambos departamentos.
11)
Se ha recibido una muestra compuesta de 100 probetas
de concreto con el objetivo de analizarlas. Una de las pruebas consistió en
determinar la carga de rotura de dichas probetas, encontrándose los siguientes resultados:
|
Intervalo
de rotura |
N°
de probetas |
|
[120 125> |
10 |
|
[125 130> |
20 |
|
[130 135> |
38 |
|
[135 140> |
25 |
|
[140 145> |
7 |
Determine :
a)
La carga media de
rotura.
b)
La carga mediana de
rotura.
Regresión lineal
1) La tabla muestra
alturas con aproximación de pulgadas y los pesos con aproximación de libras de
una muestra seleccionada al azar:
|
altura |
70 |
63 |
72 |
60 |
66 |
70 |
74 |
65 |
62 |
67 |
65 |
68 |
|
peso |
155 |
150 |
180 |
135 |
156 |
168 |
178 |
160 |
132 |
145 |
139 |
152 |
a)
Hallar la ecuación de la recta de ajuste usando
mínimos cuadrados.
b)
Estimar el peso de un estudiante cuya altura es de
61 pulgadas.
c) Estimar la altura de
un estudiante cuyo peso es de 170 libras.
![]() Solución:
Solución:
|
X |
Y |
|
|
|
X*Y |
|
70 |
155 |
4900 |
|
10850 |
|
|
63 |
150 |
3969 |
9450 |
||
|
72 |
180 |
5184 |
12960 |
||
|
60 |
135 |
3600 |
8100 |
||
|
66 |
156 |
4356 |
10296 |
||
|
70 |
168 |
4900 |
11760 |
||
|
74 |
178 |
5476 |
13172 |
||
|
65 |
160 |
4225 |
10400 |
||
|
62 |
132 |
3844 |
8184 |
||
|
67 |
145 |
4489 |
9715 |
||
|
65 |
139 |
4225 |
9035 |
||
|
68 |
152 |
4624 |
10336 |
||
|
X = 802 |
Y=1850 |
|
X*Y = 124258 |
||
![]()
![]()
![]()
![]() Calculando
a y b:
Calculando
a y b:
![]() a = -60.75
a = -60.75
b = 3.22
a)
b)Y = -60.75 +
3.22(61) = 135.67 libras. Redondeando Y =136 libras.
c) 170 = -60.75 +
3.22 X
![]() Pulgadas, redondeando X =
72 pulgadas
Pulgadas, redondeando X =
72 pulgadas
2)
La producción de acero en Estados Unidos en millones
de toneladas cortas (una tonelada corta = 2000 libras), durante los años 1946 –
1956 aparecen en la siguiente tabla:
|
Años |
Producción
en Ton. cortas |
|
1946 |
66.6 |
|
1947 |
84.9 |
|
1948 |
88.6 |
|
1949 |
78.0 |
|
1950 |
96.8 |
|
1951 |
105.2 |
|
1952 |
93.2 |
|
1953 |
111.6 |
|
1954 |
88.3 |
|
1955 |
117.0 |
|
1956 |
115.2 |
a)
Halla la ecuación de ajuste (recta de mínimos cuadrados).
b)
Estima la
producción de acero durante los años 1957 y
1958.
c) Estima la producción de acero durante los años 1945
y 1944.
Solución:
Para poder trabajar
con los años se debe colocar una escala paralela que inicie en cero (pues las
fechas no sirven para estos cálculos).
|
Años |
X |
Y |
|
|
|
X * Y |
|
|
||||||
|
1946 |
0 |
66.6 |
0 |
0 |
||
|
1947 |
1 |
84.9 |
1 |
84.9 |
||
|
1948 |
2 |
88.6 |
4 |
177.2 |
||
|
1949 |
3 |
78.0 |
9 |
234.0 |
||
|
1950 |
4 |
96.8 |
16 |
387.2 |
||
|
1951 |
5 |
105.2 |
25 |
526.0 |
||
|
1952 |
6 |
93.2 |
36 |
559.2 |
||
|
1953 |
7 |
111.6 |
49 |
781.2 |
||
|
1954 |
8 |
88.3 |
64 |
706.4 |
||
|
1955 |
9 |
117.0 |
81 |
1053 |
||
|
1956 |
10 |
115.2 |
100 |
1152 |
||
|
TOTALES |
55 |
1045.4 |
385 |
5661.1 |
||
![]() a)
Hallando la recta de ajuste
a)
Hallando la recta de ajuste
![]() a = 75.30
a = 75.30
b = 3.95
![]()
b y c) Estimando la producción:
|
Años |
X |
Producción |
|
1944 |
-2 |
67.40 |
|
1945 |
-1 |
71.35 |
|
1957 |
11 |
118.75 |
|
1958 |
12 |
122.70 |
PROBLEMAS PROPUESTOS
1)
Construir una línea recta que aproxime los datos de la tabla:
a)
|
estimar los valores de
y para: x= 11, x= 15,
x=4, x= 6
b)
estimar los
valores de
x para:
y= 2, y=5,
2) La producción de acero en Estados Unidos en
millones de toneladas cortas(1 tonelada corta = 2000 libras) durante los años 1986 – 1996 aparece en la tabla:
a) Realiza el diagrama de
dispersión.
b)
|
Determina
la ecuación de la recta de ajuste.
c)
Estima la producción de acero
durante los años: 1997 y 1998.
d)
Estima la producción de acero
durante los años: 1985 y1984
e) Halla r e interpreta.
3)
Se desea encontrar una ecuación que estime los
ingresos anuales en función de los salarios mensuales,con este fin se ha
recopilado los salarios mensuales e
ingresos anuales de 8 trabajadores de una
empresa.
|
Salarios mensuales |
100 |
150 |
200 |
275 |
300 |
325 |
350 |
375 |
|
Ingresos anuales |
1200 |
1800 |
2400 |
3300 |
3600 |
3900 |
4200 |
4500 |
a)
![]() Crea el
diagrama de dispersión respectivo.
Crea el
diagrama de dispersión respectivo.
b)
|
Determina la recta de mínimos cuadrados.
c) Estima los salarios
mensuales para aquellos trabajadores
cuyo ingreso anual es de 5700.
d)
Calcula el coeficiente de Correlación
(interpretar).
![]()
4)
La producción de cigarrillos en Perú durante los
años 1985 –1992 fue:
|
Año |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
|
N°cigarrillos (millones) |
98.2 |
92.3 |
80.0 |
89.1 |
83.5 |
68.9 |
69.2 |
7.1 |
a) Representa el diagrama de dispersión con recta de aproximación.
b)
Halla la ecuación de mínimos cuadrados.
c)
Determina e interpretar el coeficiente de Correlación
d)
Estima la producción de cigarrillos para los años 1995 y 1998.
Números índices
Problemas
propuestos:
1) La siguiente tabla
muestra los precio y cantidades de alguno cereales en los años 1989 y 1998.
![]()
1989
|
producto |
Precio |
Cantidad |
|
Cebada |
1.39 |
237 |
|
Maíz |
1.24 |
3238 |
|
Avena |
0.72 |
1220 |
|
Arroz |
0.086 |
4077 |
|
Centeno |
1.42 |
18.1 |
|
Trigo |
2.24 |
1098 |
1998
|
producto |
Precio |
Cantidad |
|
Cebada |
1.24 |
470 |
|
Maíz |
1.15 |
3800 |
|
Avena |
0.65 |
1422 |
|
Arroz |
0.097 |
4702 |
|
Centeno |
1.27 |
32.5 |
|
Trigo |
2.23 |
1462 |
A)
Tomando como base a 1989 hallar el índice de Laspeyres,
El índice de
Paashe, el índice ideal de Fisher. Para el año 1998.
B)
Tomando como base a 1989 hallar el índice de Laspeyres,
El índice de
Paashe, el índice ideal de Fisher. Para el año 1989.
C) Determine el índice
de agregación simple para los años 1989 y 1998.
2) La tabla muestra los
precios al por menor y producciones medias de antracita y gasolina en EE.UU.
durante los años 1949 y 1958.
precios
|
producto |
1949 |
1958 |
![]()
|
antracita |
$20.13
por
tonelada corta |
28.20
por
tonelada corta |
|
gasolina |
20.3 cent. Por tonelada corta. |
21.4 cent. Por tonelada corta |
cantidades
|
producto |
1949 |
1958 |
|
antracita |
3559 millones de
toneladas cortas |
1821 millones de
toneladas cortas |
|
gasolina |
80.2 millones de barriles * |
118.6 millones de barriles * |
![]() Cada barril
contiene 42 galones.
Cada barril
contiene 42 galones.
a) Determina el índice
de agregación simple para 1958 con base en 1949.
b) Determina el índice
de agregación simple para 1949 con base en 1958.
c) Halla el índice de
Laspeyres, Paashe, Fisher para el año 1958 con respecto a 1949. Interpretar.

INSTITUTO SUPERIOR TECNOLÓGICO NORBERT WIENER

Manual del
Alumno
ASIGNATURA: Estadística I
Los hombres dudan muchas veces antes de dar el primer paso,
porque piensan que no podrán alcanzar la meta que se han propuesto. Esta
actitud es el principal obstáculo que se opone a su progreso, y que cada uno de
nosotros con un pequeño esfuerzo de voluntad puede vencer.
Mahatma Gandhi
![]()
ESTADISTICA I
Índice General
Pag N° 1. Estadística General................................................................................................... 5
2.
Estadística Descriptiva........................................................ 7
3.
Las Variables Estadísticas................................................. 10
4.
La Organización de los Datos…........................................ 11
5. Práctica Calificada……..........................................................
6.
Presentación de los Datos.................................................. 24
7.
Estadígrafos de Tendencia Central.................................... 25
8.
Estadígrafos de Tendencia Central.................................... 29
9.
Estadígrafos de Tendencia No Central.............................. 35
11
Estadígrafos de Dispersión…............................................. 41
![]() 12. Distribución
Bidimensional............................................... 34
12. Distribución
Bidimensional............................................... 34
14. Regresión Lineal…............................................................ 45
15. Regresión Lineal - Análisis de Correlación....................... 49
16. Análisis de Regresión Lineal............................................. 65
17. Números Indices................................................................ 75
Problemas resueltos…............................................................ 83
10.
Problemas
propuestos....................................................... 90
![]()
SESION #1
CAPITULO I – ESTADISTICA
GENERAL
DEFINICION
Y CLASIFICACION DE LA ESTADISITICA
ESTADISTICA: Es una ciencia aplicada a cualquier tema
del saber humano y se encarga de
recopilar, ordenar, clasificar y presentar una información llamada Muestra, con
el fin de inferir acerca del comportamiento de una población.
La Estadística se clasifica en:
1.
Estadística Descriptiva; es la que se encarga de recopilar, ordenar,
clasificar y presenta una información, llamada muestra aleatoria.
2.
Estadística Inferencial; es la parte de la Estadística que se encarga de
inferir sobre el comportamiento de una población a partir de una muestra, bajo un margen de error o incertidumbre
que es cuantificado por la teoría de probabilidades.
CONCEPTOS FUNDAMENTALES EN
ESTADISTICA
POBLACION: Es
un conjunto de observaciones que tienen una característica en común la cual se
desea estudiar, la población representa la totalidad de elementos de un
determinado estudio y puede ser finita o infinita.
Ejemplos:
1.
Habitantes de Lima (aptos para el sufragio). Población Infinita
![]()
2.
Alumnos de WIENER (altura en
mts.) Población Finita
Una población si es infinita no se puede estudiar
en forma completa; aún si es finita es muy engorroso estudiarla en forma
completa por que involucra pérdida de tiempo, dinero, etc., por esta razón nos
basamos en una muestra aleatoria.
MUESTRA
Es un subconjunto de la población y para que la
muestra sea representativa debe ser aleatoria o no sesgada.
Una
muestra es aleatoria cuando cada elemento de la población tiene la misma
posibilidad de ser seleccionado en la muestra.
La
demostraremos por: n= tamaño de la
muestra ó número total de observaciones en la muestra.
Ejemplos:
1. Encuesta a 900 personas
de Lima aptos para el sufragio. n = 900
2. Altura (mts) de 45
alumnos de WIENER
n = 45.
PARAMETRO
Número
que representa a la población. Este valor generalmente es estimado a partir de
una muestra, porque para que sea calculado exactamente se requiere de la
información completa de una población lo cual es muy difícil (los procesos de
estimación de parámetros será tema de estudio en Estadística Inferencial).
ESTADIGRAFO
Llamado
también estadístico o estimador. Número que representa a la muestra y que puede
ser calculado teniendo la información de una muestra. Los Estadígrafos se
dividen en:
![]()
1. Estadígrafos de Posición o Tendencia Central: Son aquellos números que tienden al centro de las observaciones.
2. Es tadígrafos de Dispersión: Son aquellos números que cuantifican la
variabilidad de las observaciones de una muestra.
DATO:
Es la recopilación
o anotación de cada característica de las observaciones de una muestra.
Ejemplo:
Altura (mts) de n=5 alumnos de WIENER: 1.65, 1.59, 1.68, 1.63,
1.69.
SESION # 2
CAPITULO
II – ESTADISTICA DESCRIPTIVA
La Estadística Descriptiva, se encarga de recopilar
la información de una muestra aleatoria, esta información
tiene que ser ordenada para una buena presentación; Esta ordenación se basa en
las llamadas Tablas de Frecuencias y
también en los Gráficos Estadísticos.
RECOPILACION DE DATOS
Es el momento en el cual el investigador se pone en
contacto con los objetos o elementos sometidos a estudio, con el propósito de
obtener datos o respuestas de las variables consideradas; a partir de estos
![]()
datos o respuestas se calculan los Estadígrafos o
indicadores estadísticos.
FUENTES DE DATOS
La fuente de datos, es el lugar, la institución,
las personas o elementos donde están o que poseen los datos que se necesitan para
cada uno de las variables o aspectos de la investigación o estudio.
En general, se puede
disponer de cinco tipos de fuentes de datos:
1.
Las Oficinas de Estadística.- Como instituciones
responsables de recopilar, procesar y publicar las estadísticas sociales o
nacionales.
2.
Archivos o Registros Administrativos.- Como el Registro Civil,
Electoral, Escalafón o Personal, Padrón de Contribuyentes, etc.. Estos
registros no tienen fines Estadísticos, su función es de tipo legal y
administrativo, sin embargo pueden utilizarse como fuentes de datos estadísticos.
3.
Documentos.- Boletines, e informes estadísticos que son las publicaciones o estudios que preparan
los organismos especializados.
4.
Encuestas y Censos.- Son fuentes directas y especiales, que se
construyen en un momento determinado, recopilando datos de una parte o de la
totalidad de una población.
5.
Los Elementos o Sujetos.- Son aquellos que están sometidos a un estudio,
pueden ser personas, instituciones, animales u objetos.
![]()
TECNICAS DE
RECOPILACION O RECOLECCION DE DATOS
Es el conjunto de métodos y procedimientos que se
llevan a cabo para recolectar los datos.
Las más frecuentes técnicas utilizadas son:
1.
La Observación.- Es la acción de mirar de mirar en forma sistemática y
profunda, con el interés de descubrir la importancia de aquello que se observa.
2.
La Técnica Documental.- Es aquella que busca datos a través de
documentos, fuentes escritas o gráficas de todo tipo. Ejm.: Libros, Informes,
Autobiografías, fotografías, planos, videos,
etc.
3.
La Entrevista.- Es la interrelación o diálogo entre personas, donde una
de ellas se llama Entrevistador o Encuestador quien solicita a otra persona
llamada Entrevistado o Encuestado le proporcione algunos datos o información.
4.
El Cuestionario.- Es un instrumento constituido por un conjunto de
preguntas sistemáticamente elaboradas, que se formulan al Entrevistado o
Encuestado, con el propósito de obtener los datos de las variables consideradas
en el estudio. El Cuestionario se desarrolla en el Formulario o Cédula, en
donde las preguntas están debidamente organizadas.
5.
La Encuesta.- Es la técnica por la cual se obtiene la información tal
como se necesita, preparada exprofesamente y con objetivo estadístico. Permite
observar y registrar características en las unidades de análisis de una determinada población o muestra,
![]()
delimitada en el tiempo y en el espacio. El
Entrevistado da respuesta a las preguntas en el formulario o Cédula..
SESION # 3
CAPITULO
III – LAS VARIABLES ESTADISTICAS
LA VARIABLE:
Es la representación simbólica de los datos.
Ejemplo:
Sea X: altura de 5 alumnos de WIENER Donde: Xi,
i= 1 a 5 X1= 1.65 mts., X4 = 1.63 mts.
Las variables se
clasifican en:
I.
Variable Cualitativa: Es aquella variable que representa a datos que
indican cualidades, características, propiedades, etc., no son numéricas (no medibles).
Ejemplos:
X = Control de calidad de productos de una industria. Bueno, Malo, Regular, Muy Bueno.
Y = Estado Civil de una muestra de 200
personas. Soltero, Casado, Viudo, Divorciado.
II.
Variable Cuantitativa: Es aquella variable que representa a datos que
indican valores numéricos (son medibles), y se clasifican en:
![]()
Variable Discreta: Es aquella que representa a datos numéricos que no
se pueden fraccionar, sirven para contar o enumerar (pertenecen a los reales).
Variable Continua: Es aquella variable que representa a datos
que pueden ser fraccionados (pertenecen a los reales).
Ejemplo: El Peso (Kg.) de 6 personas. 65, 56,
59, 70, 63.
La variable continua es la que más utilizamos,
especialmente para los estudios correspondientes en Ingeniería (Volumen,
Temperatura, Pesos, Mediciones, etc.).
SESION # 4
CAPITULO
IV – LA ORGANIZACIÓN DE LOS DATOS
Distribución o Tablas de Frecuencias: Es la condensación, simplificación, ordenación, del
conjunto de observaciones que forman la muestra; la característica principal es
no perder ningún dato de la muestra.
También se puede decir que la Distribución de Frecuencia es la
representación estructurada, en forma de tabla, de toda la información que se
ha recogido sobre la variable que se estudia.
![]() Categorías
o Clases.- Son los datos que están agrupados por sus características comunes.
Categorías
o Clases.- Son los datos que están agrupados por sus características comunes.
![]()
Frecuencia de Clases.- Es el número o cantidad de datos que componen
una Categoría o Clase. Las Frecuencias se clasifican en :
1.
Frecuencia Absoluta (Simple).- Representa a
la cantidad de datos de cada Clase.
2.
Frecuencia Absoluta Acumulada.- Representa a
la suma en forma acumulativa de Clase en
Clase de sus respectivas Frecuencias Absolutas.
3.
Frecuencia Relativa (Simple) .- Es el % que
representa a la cantidad de datos de una Clase con respecto al total de datos.
4.
Frecuencia Relativa Acumulada.- Representa a
la suma en forma acumulativa de Clase en Clase de sus respectivas Frecuencias
Relativas.
Veamos un ejemplo
(4.1) :
Medimos la altura de los niños de una clase y
obtenemos los siguientes resultados (cm):
|
Alumno |
Estatura |
Alumno |
Estatura |
Alumno |
Estatura |
|
|
|
|
|
|
|
|
Alumno 1 |
1,25 |
Alumno 11 |
1,23 |
Alumno 21 |
1,21 |
|
Alumno 2 |
1,28 |
Alumno 12 |
1,26 |
Alumno 22 |
1,29 |
|
Alumno 3 |
1,27 |
Alumno 13 |
1,30 |
Alumno 23 |
1,26 |
|
Alumno 4 |
1,21 |
Alumno 14 |
1,21 |
Alumno 24 |
1,22 |
|
Alumno 5 |
1,22 |
Alumno 15 |
1,28 |
Alumno 25 |
1,28 |
|
Alumno 6 |
1,29 |
Alumno 16 |
1,30 |
Alumno 26 |
1,27 |
|
Alumno 7 |
1,30 |
Alumno 17 |
1,22 |
Alumno 27 |
1,26 |
|
Alumno 8 |
1,24 |
Alumno 18 |
1,25 |
Alumno 28 |
1,23 |
|
Alumno 9 |
1,27 |
Alumno 19 |
1,20 |
Alumno 29 |
1,22 |
|
Alumno 10 |
1,29 |
Alumno 20 |
1,28 |
Alumno 30 |
1,21 |
Si presentamos esta información estructurada
obtendríamos la siguiente Tabla de Frecuencias:
![]()
|
Variable |
Frecuencias
Absolutas |
Frecuencias
Relativas |
||
|
(Valor) |
Simple |
Acumulada |
Simple |
Acumulada |
|
|
|
|
|
|
|
1,20 |
1 |
1 |
3,3% |
3,3% |
|
1,21 |
4 |
5 |
13,3% |
16,6% |
|
1,22 |
4 |
9 |
13,3% |
30,0% |
|
1,23 |
2 |
11 |
6,6% |
36,6% |
|
1,24 |
1 |
12 |
3,3% |
40,0% |
|
1,25 |
2 |
14 |
6,6% |
46,6% |
|
1,26 |
3 |
17 |
10,0% |
56,6% |
|
1,27 |
3 |
20 |
10,0% |
66,6% |
|
1,28 |
4 |
24 |
13,3% |
80,0% |
|
1,29 |
3 |
27 |
10,0% |
90,0% |
|
1,30 |
3 |
30 |
10,0% |
100,0% |
Si los valores que toma la variable son muy
diversos y cada uno de ellos se repite muy pocas veces, entonces conviene
agruparlos por intervalos, ya que de otra manera obtendríamos una tabla de
frecuencia muy extensa que aportaría muy poco valor a efectos de síntesis.
Según los tipos de variables y formas de la tabla
de frecuencias, tendremos las siguientes Tablas de frecuencias
1ER. CASO:
Tablas de Frecuencias para la variable Cualitativa:
En
este caso como la variable cualitativa indica cualidades, propiedades, etc., y
no son medibles; entonces se agrupa de acuerdo a cada categoría que se
diferencia en la variable cualitativa. (Sin un orden establecido).
Ejemplo: (4.2).
![]()
![]()
![]()
![]()
![]()
Se tiene la
siguiente información que representa el Estado Civil de 50 personas encuestadas
(edad; 20-30 años).
|
Estado Civil |
No. de personas |
% |
|
Soltero |
25 |
50% |
|
Casado |
10 |
20% |
|
Viudo |
1 |
2% |
|
Divorciado |
6 |
12% |
|
Conviviente |
8 |
16% |

![]() Los gráficos que se
presentan en este caso son los siguientes: 1). Diagrama de barra:
Los gráficos que se
presentan en este caso son los siguientes: 1). Diagrama de barra:
2. Gráfico por Sectores Circulares.

2DO. CASO: Tabla de frecuencia para la variable discreta y n
< 30 :
En
este caso la variable es discreta y la muestra pequeña, además hay que
considerar que no haya muchos datos diferentes. La Tabla de frecuencias es por
CLASES, donde cada clase representa el valor numérico de la variable.
![]()
La tdf es de la sgte. forma general:
|
Clase Xi |
Fi |
Fi |
hi |
Hi |
|
x1 |
f1 |
F1 |
h1 |
H1 |
|
x2 |
f2 |
F2 |
h2 |
H2 |
|
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
|
Xm |
Fm |
Fm=n |
hm |
.Hm=1 |
Donde:
n = numero de clases o intervalos de clase.
fi = frecuencia absoluta: es el número de
observaciones que hay en cada clase o intervalo de clase. Además:
fi+f2+f3+.... + fm =n

Fi = frecuencia absoluta acumulada: es
el numero de observaciones acumuladas hasta la clase i, es decir:
F1=f1 F2=f1+f2
.
.
![]()
Fm=f1+f2+f3...+fm =
hi = frecuencia relativa: representa la
relación que existe entre la frecuencia absoluta y el número total de
observaciones:

Generalmente la
frecuencia relativa se expresa en forma porcentual: hi % = 100%.
Hi = frecuencia relativa acumulada: frecuencias relativas acumuladas hasta la clase i.
Hi=h1 H2=h1+h2
.
. Hm=h1+h2+....hm=1
 También :
También :
Se expresa en forma
porcentual. Hi x 100%
Ejemplo:
![]()
Los siguientes datos representan el numero de
defectos en 15
diskettes: 5, 10, 5, 11,6,6,3,3,3,5,5,5,10,6,3.
Agrupar en tabla de
frecuencias:
Solución:
Como la muestra es pequeña y la variable representa
a datos discretos, entonces agrupamos en clases:
|
No de Defectos Xi |
No. diskettes fi |
Fi |
hi% |
Hi% |
|
3 |
4 |
4 |
26.7 |
23.7 |
|
5 |
5 |
9 |
33.3 |
60.0 |
|
6 |
3 |
12 |
20.0 |
80.0 |
|
10 |
2 |
14 |
13.3 |
93.3 |
|
11 |
1 |
15 |
6.7 |
100.0 |
Los gráficos que se presentan en este 2do. Caso
son:
![]() 1. Histograma de
frecuencias: En el sistema de coordenadas rectangulares comparamos
Xi vs. fi (o hi%).
1. Histograma de
frecuencias: En el sistema de coordenadas rectangulares comparamos
Xi vs. fi (o hi%).

![]() 3ER. CASO: Tabla de frecuencias por intervalos de clase:
3ER. CASO: Tabla de frecuencias por intervalos de clase:
En este caso generalmente la variable es continua,
también puede ser usado para la variable discreta siendo la muestra grande (generalmente n >= 30).
La tdf tiene la siguiente forma:
|
Intervalos (Li - Ls) |
Xi |
Fi |
Fi |
hi |
Hi |
|
[X’o - X’1> |
X1 |
f1 |
F1 |
h1 |
H1 |
|
[X’1 - X’2> |
X2 |
f2 |
F2 |
h2 |
H2 |
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
|
. |
. |
. |
. |
. |
. |
|
[X’m-1- X’m] |
Xm |
Fm |
Fm |
hm |
Hm |
Donde:
![]()
X i= marca de clase o
punto medio de cada intervalo de clase, se obtiene mediante la semisuma de los
limites de cada intervalo.
X i = Ls
+ Li
2
fi , Fi, hi, Hi ; representan las frecuencias definidas en el
caso anterior.
Procedimiento
para construir una tdf por intervalos de clase:
1er. Paso:
Calcular el número de intervalos de clase (K):
Para calcular el valor de K, tenemos dos criterios:
a)
Criterio personal; de acuerdo a la experiencia del investigador se puede
asumir un valor de m para un tamaño de muestra
determinado.
b)
Mediante la Regla de Sturges:
K =1 +3.3 log. n
2do. Paso:
Calcular la amplitud o tamaño del intervalo de
clase:(A)
Para calcular la
amplitud del intervalo (A) nos basaremos en la siguiente expresión:
![]()
A = Rango de la
muestra
K
donde: Rango de la muestra = Valor Mayor – Valor
Menor
Con este procedimiento calculamos una amplitud que
será constante para cada intervalo, y lo mismo ocurrirá entre cada marca de
clase.
Los intervalos serán de la forma: [Li
Ls], pudiendo ser considerado cerrado en el último intervalo.
La amplitud A es
preferible que sea redondeada considerando la misma cantidad de decimales que
tengan los dato de la muestra.
3er. Paso: Tabulaciones
Tabular y presentar los datos agrupados en la
tdf.,
Ejemplos: (2.3)
Los siguientes datos
representan el peso (gr.) de 35 sobrecitos
de unas sustancias: 68, 73, 61, 46, 49,
96, 68, 90, 97, 53, 75, 93, 72, 60,
71, 75, 74, 75, 71, 77, 83, 68, 85, 76, 88, 59, 78, 62, 55, 48, 43, 47,
60, 84, 80. Agrupar en tdf. Solución:
1) Calculamos K = 1 +3,3 Log
35 = 6.095 = 6
2)
Calcula la amplitud del intervalo A:
![]()
![]() A 97 43 9
A 97 43 9
6
![]()
3)
Tabular en
tdf:
|
Peso (grs) |
Xi |
fi |
Fi |
hi% |
Hi% |
|
[43 – 52> |
47.5 |
5 |
5 |
14.3 |
14.3 |
|
[52 – 61> |
56.5 |
5 |
10 |
14.3 |
28.6 |
|
[61 – 70> |
65.5 |
5 |
15 |
14.3 |
42.9 |
|
[70 – 79> |
74.5 |
11 |
26 |
31.4 |
74.3 |
|
[79 – 88> |
83.5 |
4 |
30 |
11.4 |
85.7 |
|
[88 – 97] |
92.5 |
5 |
35 |
14.3 |
100.0 |
Se observa por ejemplo
que: 11 sobrecitos tienen un peso comprendido en el intervalo [70-79> grs. y
representan el 31.4% del total.
También vemos que 15 sobrecitos pesan menos de 70
grs. y representan el 42.9% del total.
![]()
SESION # 5
PRIMERA
PRACTICA CALIFICADA
SESION # 6
PRESENTACION
DE DATOS
LOS GRAFICOS
Los gráficos son representaciones en forma de
figuras geométricas, de superficie o volumen con el objeto de ilustrar los
cambios o dimensión de una variable, para comparar visualmente dos o más
variables similares o relacionadas. Para una rápida comprensión de situaciones
o variaciones en cantidades, es muy útil traducir los números en gráficos o
imágenes. Por su naturaleza, un gráfico no toma en cuenta los detalles y no
tiene la misma precisión que una tabla estadística.
Veamos algunos tipos de Gráficos :
1.
Histograma
de frecuencias: Representa un conjunto de rectángulos levantados desde cada intervalo de
clase hasta la frecuencia correspondiente (absoluta ó relativa).
2.
Polígono
de frecuencias: Consiste en unir los puntos medios ó marcas de clase levantadas hasta
cada frecuencia correspondientes, generalmente para su construcción nos podemos
basar del Histograma de frecuencias.
Propiedad:
Area del Histograma = Area del Polígono de frecuencia.
3.
Ojiva: Se
construye basándose en un diagrama escalonado, es decir considerando las
frecuencias acumuladas (absoluta ó relativa), y uniendo los límites de cada intervalo.
 HISTOGRAMA Y POLIGONO DE FRECUENCIAS
HISTOGRAMA Y POLIGONO DE FRECUENCIAS

SESION # 7
LOS
ESTADIGRAFOS DE TENDENCIA CENTRAL
Se
llaman así, porque tienden a ubicar el centro de las observaciones; Estos
estadígrafos de posición son: media, mediana, moda, media geométrica, media
armónica, etc. Estudiaremos los más importantes:
![]() 1. La Media Aritmética
1. La Media Aritmética
Llamada también promedio, es el estadigrafo de
posición más simple y fácil de calcular, por eso es el más común.
Se calcula teniendo en
cuenta los siguientes casos:
1er. Caso: Datos no agrupados en tablas de frecuencias:
Sean X1, X2........... , Xn variables que representan
los n datos de una

muestra, la media
aritmética se calcula:
2do. Caso: Datos
Agrupados en tabla de frecuencias:
 En este caso se calcula mediante la siguiente fórmula:
En este caso se calcula mediante la siguiente fórmula:
fi
= frec. Absoluta hi = frec. Relativa
.
 O también:
O también:
|
|
![]()
hi = frec. Relativa
PROPIEDADES DE LA MEDIA ARITMETICA
1. La
media de los datos todos iguales a una misma constante es igual a la constante:
Sea K = cte. y
cada Xi = k -----------------
X X (K ) K
2. ![]()
![]() Si a cada dato e le
suma o resta una constante k, la media queda
sumada o restada por dicha constante:
Si a cada dato e le
suma o resta una constante k, la media queda
sumada o restada por dicha constante:
![]()
![]()
![]()
Si Xi = Xi +
K -------------------- X(Y) = X(X+k) =
X (X) + k
3. Si a cada dato se le
multiplica o divide por una constante k, la media queda multiplicada o dividida
por dicha constante.
![]()
![]()
![]()
4. Sí Yi = Xi*
k---------------------------- X(Y)
= X(X* k) = X (X) * k
NOTA. Todas las propiedades cumplen para datos agrupados
y no agrupados
![]()
![]()
![]()
![]() ( Xi X
) 0
( Xi X
) 0
Datos no agrupados
![]()
![]() ( Xi
( Xi
X )* fi 0
5. La suma de las
desviaciones respecto a la media es
igual a cero.
SESION # 8
ESTADIGRAFOS
DE TENDENCIA CENTRAL
2. Media Geométrica: se eleva cada valor al número de veces que se ha
repetido. Se multiplican todo estos resultados y al producto final se le
calcula la raíz "n" (siendo "n" el total de datos de la
muestra).
![]()
Según el tipo de datos que
se analice será más apropiado utilizar la media aritmética o la media
geométrica.
La media geométrica se suele utilizar en series de
datos como tipos de interés anuales, inflación, etc., donde el valor de cada
año tiene un efecto multiplicador
sobre el de los años anteriores. En todo caso, la media aritmética es la medida
de posición central más utilizada.
Lo más positivo de la media es que en su cálculo se
utilizan todos los valores de la
serie, por lo que no se pierde ninguna información.
Sin embargo, presenta el problema de que su valor
(tanto en el caso de la media aritmética como geométrica) se puede ver muy
influido por valores extremos, que se aparten en exceso del resto de la serie.
Estos valores anómalos podrían condicionar en gran medida el valor de la media,
perdiendo ésta representatividad.
3. La Mediana (Me) :
Es aquel estadígrafo de posición que divide en dos
partes iguales al conjunto de observaciones; es decir la mediana representa el
valor central de una distribución de datos ordenados en forma creciente o
decreciente.
1er. Caso: Datos No agrupados en TDF:
Primero se
ordena los datos en forma creciente o decreciente y luego se tiene en cuenta
sí:
a) n es impar. La mediana es el
valor central.
![]()
 Es el elemento
que ocupa la posición (n+1) /2
Es el elemento
que ocupa la posición (n+1) /2
Ejemplo: Calcular la Me de los siguientes valores:
32, 34, 31, 42, 36, 41,
32, 45, 37, n=9
Ordenando: 31, 32, 32,
34, 34, 36, 37, 41, 42, 45.
Observamos el valor
central:
Me=36 (representa
el 5to. dato)
b) n es par.La mediana es igual al
promedio o la semisuma de los valores centrales.
Ejemplo: la Me de 12,21,16,18,20,19,16,15,16,17.
![]() Ordenando: 12,15,16,16,16,17,18,19,20,21,
Ordenando: 12,15,16,16,16,17,18,19,20,21,
![]()
2do. Caso: Datos Agrupados en TD:
![]()
 En este caso la Se me calcula mediante la siguiente fórmula:
En este caso la Se me calcula mediante la siguiente fórmula:
![]()
Donde:
Li = limite inferior de
la clase mediana.
Ame := tamaño del intervalo de la clase mediana.
Fme-1 = Frec. Abs. Acumulada anterior a la clase mediana.
fme = Frecuencia
absoluta de la clase mediana.
Clase Mediana: Es aquel intervalo que contiene el valor que ocupa la posición media, es
decir contiene a la mediana. Se calcula mediante:
El primer valor Fi mayor o igual que n/2
4. LA MODA (Mo)
Representa al valor
que más se repite en un conjunto de observaciones:
-
Si la distribución de frecuencias tiene un solo valor máximo, entonces: UNIMODAL.
-
Si la distribución presenta más de un valor máximo: , entonces: POLIMODAL.
-
Si no hay algún valor que se repita con más frecuencia: DISTRIBUCION UNIFORME
1er. Caso: Datos no
agrupadas
Señalar el valor que más se repite.
Ej. 4,5,6,7,4,5,4,6,5,5,4,5,5 Mo = 5 UNIMODAL
Ej. 7,7,6,8,8,6,8,7,7,9,12,11,10,8Mo = 8
BIMODAL
2do. Caso: Datos
Agrupados en Tablas de Frecuencias_

![]()
Donde:
Li = limite
inferior de la clase modal. Amo = Amplitud
de la clase modal.
D1 = Diferencia ente la
Frec. Absoluta de la clase modal menos la frecuencia absoluta anterior.
D2 = Diferencia ente la
Frec. Absoluta de la clase modal
menos la siguiente.
Clase Modal: Representa el intervalo con la mayor
frecuencia absoluta.
Ejemplos. (3.1)
![]()
Calcular la Media
Aritmética, Mediana y Moda de la Tabla de frecuencias del ejemplo (2.3).
![]() gramos
gramos
Para calcular la mediana, la clase mediana es el 4to. intervalo:
 gramos
gramos
Para calcular la Moda,
la clase modal es el 4to. intervalo, por que presenta la mayor frecuencia
absoluta.
D1=11 - 5 = 6
D2=11 – 4 =7
![]() Mo 70
Mo 70
9 * 6
![]()
![]() 6 7
6 7
74.15
Gramos
Nota: La media =mediana = moda, si la
distribución es simétrica.
SESION # 9
![]()
ESTADIGRAFOS DE TENDENCIA NO CENTRAL
Las medidas de Posición o de Tendencia no
centrales permiten conocer otros puntos característicos de la distribución que
no son los valores centrales. Entre otros indicadores, se suelen utilizar una
serie de valores que dividen la muestra en tramos iguales:
Cuartiles: son 3 valores que
distribuyen la serie de datos, ordenada de forma creciente o decreciente, en
cuatro tramos iguales, en los que cada uno de ellos concentra el 25% de los
resultados.
Percentiles: son 99 valores que
distribuyen la serie de datos, ordenada de forma creciente o decreciente, en
cien tramos iguales, en los que cada uno de ellos concentra el 1% de los
resultados.
![]()
aunque haría falta distribuciones con mayor
número de datos.
|
Variable |
Frecuencias
absolutas |
Frecuencias
relativas |
||
|
(Valor) |
Simple |
Acumulada |
Simple |
Acumulada |
|
X |
x |
x |
x |
X |
|
1,20 |
1 |
1 |
3,3% |
3,3% |
|
1,21 |
4 |
5 |
13,3% |
16,6% |
|
1,22 |
4 |
9 |
13,3% |
30,0% |
|
1,23 |
2 |
11 |
6,6% |
36,6% |
|
1,24 |
1 |
12 |
3,3% |
40,0% |
|
1,25 |
2 |
14 |
6,6% |
46,6% |
|
1,26 |
3 |
17 |
10,0% |
56,6% |
|
1,27 |
3 |
20 |
10,0% |
66,6% |
|
1,28 |
4 |
24 |
13,3% |
80,0% |
|
1,29 |
3 |
27 |
10,0% |
90,0% |
|
1,30 |
3 |
30 |
10,0% |
100,0% |
2º
cuartil: es el valor 1,26 cm, ya que entre este valor y el 1º cuartil se situa
otro 25% de la frecuencia.
![]()
Atención: cuando un cuartil
recae en un valor que se ha repetido más de una vez (como ocurre en el ejemplo
en los tres cuartiles) la medida de posición no central sería realmente una de
las repeticiones
Fórmulas para calcular los Cuartiles

![]() Q1 Li
Q1 Li
F 2

![]() Q2 Li
Q2 Li
F 2
Para calcular el Tercer Cuartil
Q3 Li

![]() F 2
F 2
Q1 = Primer Cuartil Q2 = Segundo Cuartil Q3 = Tercer Cuartil

![]()
Li = Límite Real inferior de la Clase que contiene el
Cuartil n = Número de datos
F1 = Frec. Acumulada de la clase anterior a la clase del
Cuartil F2 = Frecuencia absoluta de la Clase del Cuartil
i = Intervalo de Clase
Ejemplo: Calcular el Primer Cuartil de la siguiente
distribución de frecuencias, referente al consumo de energía eléctrica de un
grupo de usuarios
|
Consumo Kw Hora |
Número de Consumidor |
Frecuencia Acumulada |
Límites Reales |
|
05 - 24 |
4 |
4 |
4.5 - 24.5 |
|
25 - 44 |
6 |
10 |
24.5 - 44.5 |
|
45 - 64 |
14 |
24 |
44.5 - 64.5 |
|
65 - 84 |
22 |
46 |
64.5 - 84.5 |
|
85 - 104 |
14 |
60 |
84.5 - 104.5 |
|
105 - 124 |
5 |
65 |
104.5 - 124.5 |
|
125 - 144 |
7 |
72 |
124.5 - 144.5 |
|
145 - 164 |
3 |
75 |
144.5 - 164.5 |
|
|
75 |
|
|

Como cada Cuartil representa el 25%, entonces el Primer
Percerntil será el 25%.
Respuesta.- El 25% de los usuarios
consume 57 KW Hora.
CURSO: ESTADISTICA I
![]()
D = El Decil
Li = Límite Real inferior de la Clase que contiene el
Decil D # = El número de Decil que se quiere
hallar
n = Número de datos
F1 = Frec. Acumulada de la clase anterior a la clase del
Cuartil F2 = Frecuencia absoluta de la Clase del Cuartil
i = Intervalo de Clase
Utilizando el ejemplo: Calcular el Cuarto Decil de
la distribución de frecuencias, referente al consumo de energía eléctrica del
grupo de usuarios

Como cada Decil representa el 10%, entonces el Cuarto
Decil será el 40%..
Respuesta.- El 40% de los usuarios
consume 69.95 KW Hora.

P = El Percentil
Li = Límite Real inferior de la Clase que contiene el Percentil
![]()
P # = El número de Percentil que se quiere hallar n =
Número de datos
F1 = Frec. Acumulada de la clase anterior a la clase del
Percentil F2 = Frecuencia absoluta de la Clase del Percentil
i = Intervalo de Clase
Utilizando el ejemplo: Calcular el
Percentil 79 de la distribución de frecuencias, referente al consumo de energía
eléctrica del grupo de usuarios

Como cada Percentil representa el 1%, entonces el
Percerntil 79 será el 79%..
Respuesta.- El 79% de los usuarios
consume 103.43 KW Hora.
SESION # 10
EXAMEN PARCIAL
SESION # 11
ESTADIGRAFOS
DE DISPERSION O VARIABILIDAD
Son
aquellos números que miden o cuantifican la variabilidad de las observaciones,
con respecto a un estadígrafo posición (generalmente la media aritmética). Los
principales estadígrafos de dispersión son los siguientes:
1. LA VARIANZA:
V (X)


Se
define como el promedio del cuadrado de las desviaciones con respecto a la
media.
![]()
![]() Cuando la varianza es muestral, entonces V(x) se puede denotar como y si la varianza es poblacional, entonces
V(x) se denota como .En este capítulo estudiaremos la varianza
Cuando la varianza es muestral, entonces V(x) se puede denotar como y si la varianza es poblacional, entonces
V(x) se denota como .En este capítulo estudiaremos la varianza
muestral.
La varianza se
calcula, teniendo en cuenta los siguientes casos:
1er. Caso: Datos no agrupados en tablas de frecuencia:
|
|
|
|
Desarrollando esta
sumatoria, obtenemos una forma más simple para calcular la varianza:

I
2do.
Caso: Datos agrupados en tablas de frecuencias:
 O también:
O también:
![]()
CURSO: ESTADISTICA I
![]()
Desarrollando esta
sumatoria, obtenemos:

O también:

|
Donde: |
|
|
|
Xi |
= |
marca
de clases. |
|
fi |
= |
frecuencia absoluta |
|
hi |
= |
frecuencia relativa |
Propiedades de la Varianza:
1.
V(X) >= 0 (siempre
la varianza es positiva ó
igual a cero).
|
2, |
V(K) = 0 |
Esto es si cada Xi = k (constante). |
|
3. |
V(X+/- K) = V(X) |
si a cada Xi se le suma (o resta), |
|
|
una constante K |
entonces la varianza no varia. |
![]() 4.
4.
![]() CURSO: ESTADISTICA I
CURSO: ESTADISTICA I
si
a cada dato se multiplica (o por una constante K, entonces la
constante sale elevada cuadrado).
Siendo
a y b constantes, X e Y variables independientes
![]()
5.
2.
DESVIACION
STANDART O TIPICA : S(X)
Se
define como la raíz cuadrada positiva de la varianza, y como la varianza esta
expresada en unidades cuadradas, la desviación standart (que esta expresada en
las mismas unidades de los datos), representa mejor la variabilidad de las
observaciones.

3.
COEFICIENTE DE VARIACION: C.V.
Representa la
relación que existe entre la desviación standart y el promedio de un conjunto
de observaciones. El C.V. como no tiene unidades se debe expresar en porcentaje
y sirve como medios de comparación con otras distribuciones de cualquier tipo
de unidad.
Se calcula:

Donde:
S(x) = desviación típica
X = promedio aritmético ó
Ejemplos:
1.
Los siguiente datos son temperaturas en grados Fahrenheit
415,500,480,490,476,500,432,479,489,497,496,478,453.
Sin ordenar en
tablas de frecuencias:
a) Calcular la varianza.
b)
Si a cada dato se le divide entre 5 y luego se suma
10. Hallar la nueva varianza.
Solución:
a)
Primero tenemos que calcular el promedio para datos
no agrupados:
 °F
°F
Entonces,
calculamos la varianza:
b)
![]() Es decir:
Es decir:

Esto se resuelve
usando propiedades:
2. Dada la siguiente
tabla de frecuencias, que representa el peso (grs), de 34 sobres de cartas:
|
Intervalos |
Xi |
fi |
Fi |
|
[ 7 – 8> |
7.5 |
1 |
1 |
|
[ 8 – 9> |
8.5 |
2 |
3 |
|
[ 9 – 10> |
9.5 |
8 |
11 |
|
[10 – 11> |
10.5 |
11 |
22 |
|
[11 – 12> |
11.5 |
6 |
28 |
|
[12 – 13] |
12.5 |
6 |
34 |
a)
Calcular el peso promedio y la mediana.
b)
Calcular el Coeficiente de Variación (C.V.)
Solución:
a)
Calculando el
promedio:
Calculando
la mediana:
![]() Gramos
Gramos
b)
Para calcular el
C.V. debemos primero calcular la varianza
![]()
Calculamos la
desviación standart: S(X)=-1.2708 grs. Entonces:
![]()
3. Se tiene dos muestras:
En qué muestra cree
Ud. Que halla menos variabilidad?
![]()
![]()
![]()
![]()
![]()
![]()
Solución:
Primero
hay que tener en cuenta que no se puede comparar las desviaciones standares de
cada nuestra, porque están expresadas en
diferente unidades, pero si podemos compararlas con sus C.V. respectivos:
![]()
![]()
Entonces,
comprando ambos coeficientes nos damos cuenta que existe menor dispersión en
los datos de la primera muestra.
![]()
SESION # 12
CAPITULO V:
DISTRIBUCION BIDIMENSIONAL
ANALISIS
DE REGRESION Y CORRELACION LINEAL SIMPLE
Los
métodos estadísticos presentados lo hemos referido hasta Ahora a una sola
variable, muchos de los problemas de trabajo estadístico, sin embargo
involucran 2 ó más variables. En algunos casos las variables se estudian
Simultáneamente, para ver la forma en que se encuentran interrelacionadas,
también si se desea estudiar una variable de interés particular. Estos dos
casos de problemas se conocen por lo general con los nombres de correlación y regresión.
Antes
de definir estos casos hablaremos sobre aspectos importantes que involucran 2
variables: Distribución Bidimensional.
5.1. Cálculo de la
Covarianza: S (XY)
La
varianza, es la medida que estudia la dispersión de dos variables, se calcula
teniendo en cuenta:
1er.
Caso: Datos no agrupados en tablas de frecuencia: En este
caso, las variables X é Y se toman en forma simultánea; es decir se considera
no agrupados porque se toman los valores
![]()
como puntos cartesianos (pares de valores). (X1,Y2),
(X2,Y2). (Xm,Ym). Esto es:
|
X |
X1 |
X2 |
X3 |
.......... |
XN |
|
Y |
Y1 |
Y2 |
Y3 |
.......... |
YN |
N: número de
observaciones ó total de pares de valores.
 De cada observación se analiza dos variables Simultáneamente. Las
Covarianza; S (XY) se define:
De cada observación se analiza dos variables Simultáneamente. Las
Covarianza; S (XY) se define:
.............................
( I )
desarrollando la
sumatoria y simplificando:

![]()
Para
calcular la covarianza S(XY), es preferible utilizar la ec. (II). Los promedios
de X y de Y, así como las desviaciones standares S(X) Y S(Y), se calculan
como en los capítulos 3 y 4.
2do. Caso: Datos
Agrupados en tablas de frecuencias:
En
este caso cada variable X e Y, están agrupados en tablas de frecuencias
presentándose lo que se llama: Distribución Bidimensional o Tabla de Doble
Entrada.
En forma tabular:
X : agrupado en K intervalos (y = 1... k)
Y : agrupado
en m intervalos (j = 1.. m).
Donde:
Xi : marca de clase (variable X) Yj : marca
de clase (variable Y)
fij : frecuencia absoluta conjunta,
corresponde al número de observaciones que existe en el I-ésimo intervalo de X con el j-ésimo
intervalo de Y.
Observaciones:
(1)
Según la definición de la covarianza (tanto para
datos agrupados como no agrupados), la covarianza puede ser negativa.
(2)
La covarianza presenta unidades de cada una de las
variables involucradas.
(3)
La covarianza S(XY), también se denota: Cov (X,Y)
![]()
Ejemplos:
(5.1) Dada la
siguiente tabla, que representa la medida (X) en cm. De 8 barretas de metal y
el peso (Y) en libras de cada una de ellas, calcular:
a) S(X) b) S(Y) c) S(XY)
|
X |
1 |
3 |
4 |
6 |
8 |
9 |
11 |
14 |
|
Y |
1 |
2 |
4 |
4 |
5 |
7 |
8 |
9 |
Solución:
Este ejemplo,
corresponde a datos no agrupados en tabla de frecuencias.
a)
S (X) = 4.06![]()
S2 (X)
=
b) S (Y) = 2.65![]()
S2 (Y)
![]()
![]()
![]()
(5.2) Dada la
siguiente tabla en el cual se estudia las alturas (pulg) y los pesos (libras)
de 300 estudiantes hombres en una Universidad:
X
: altura (pulgadas).
Y
![]()
![]() : peso (libras).
: peso (libras).
|
Y X |
58-62 |
62-66 |
66-70 |
70-74 |
74-78 |
Total fy |
|
90-110 |
2 |
1 |
|
|
|
3 |
|
100-120 |
7 |
8 |
4 |
2 |
|
21 |
|
130-140 |
5 |
15 |
22 |
7 |
1 |
50 |
|
50-160 |
2 |
12 |
63 |
19 |
5 |
101 |
|
170-180 |
|
7 |
28 |
32 |
12 |
79 |
|
190-200 |
|
2 |
10 |
20 |
7 |
39 |
|
210-220 |
|
|
1 |
4 |
2 |
7 |
|
Total Fx |
16 |
45 |
128 |
84 |
27 |
300 |
Calcular:
![]()
S (X) , S(Y) , S (XY)
Solución:
Como
la tabla es Bidimensional, podemos formar tablas de frecuencias para cada una
de las variables por separado, a este proceso se le conoce como TABLAS
MARGINALES.
Tabla marginal para
x::
|
Intervalos |
Xi |
Fi |
|
58 – 62 |
60 |
16 |
|
62 – 66 |
64 |
45 |
|
66 – 70 |
68 |
128 |
|
70 – 74 |
72 |
84 |
|
74 – 78 |
76 |
27 |
300
Tabla Marginal para Yi:
|
Intervalos |
Yj |
f.j. |
|
90 – 110 |
100 |
3 |
|
110 – 130 |
120 |
21 |
|
130 – 150 |
140 |
50 |
|
150 – 170 |
160 |
101 |
|
170 – 190 |
180 |
79 |
|
190 – 210 |
200 |
39 |
|
210 – 230 |
220 |
7 |
300
La variable X presenta 5 intervalos ( i = 1..... 5)
La variable Y presenta 7 intervalos ( j = 1..... 7)
Calculando:


S(XY) =51.370 pulg/lib.
Calculando la Covarianza:

![]()
![]()
![]()
SESION # 14
REGRESION LINEAL
5.2. Diagrama de
Puntos y Curvas de Ajuste:
Representan
los puntos (X1, Y1), (X2, Y2)..... (XN, YN) en un sistema de coordenadas
rectangulares, donde al sistema de puntos resultantes lo llamaremos Diagrama
de Dispersión o Diagrama de Puntos: Con el diagrama de dispersión es
posible representar una curva que se aproxime a los datos: Curva de
Aproximación.
Entonces, encontrar
ecuaciones de curvas de aproximaciones que se ajusten a los datos, es buscar
una: Curva
de Ajuste.
Tenemos:
a) Conjunto de puntos
que se ajustan a una línea recta (ajuste lineal o relación lineal).

Observamos que el
diagrama de puntos gira alrededor de una recta: Y = a+ bX
![]()
b) Conjunto de puntos o
diagrama de puntos cuya relación no es lineal.

Algunas de las
ecuaciones de curvas de aproximación:
![]()
 Relación
lineal
Relación
linealCurva Polinomial
Hipérbola
Entonces,
lo que se desea es encontrar una curva de aproximación que se ajuste mejor a los datos, y así mostrar la
ecuación de la curva respectiva.
El
tipo más sencillo de una curva de aproximación es la línea recta cuya ecuación
puede escribirse: Y = a +b*X
![]()
5.3 Método de mínimos Cuadrados:
![]() De todas las curvas de aproximación a una serie de datos puntuales, la
curva tiene la propiedad de que:
De todas las curvas de aproximación a una serie de datos puntuales, la
curva tiene la propiedad de que:
sea mínimo
Se conoce como la mejor curva de ajuste por
el método de mínimos cuadrados.
Di= desviación de
cada punto con respecto ala línea recta.
Este método
consiste en minimizar la suma de los cuadrados de las desviaciones Di.
Entonces
para ajustar un diagrama de dispersión a la línea recta, utilizaremos este
método de los MINIMOS CUADRADOS. Es decir una recta de aproximación de mínimos
cuadrados del conjunto de puntos (x1, y1), (x2,y2),......,(xn,yn), tiene la
ecuación: Y = a+b*X , donde a y b se determinan mediante el sistema de
ecuaciones normales, son las siguientes:

Donde al desarrollar y despejar a
y b se obtienen:


Otras
ecuaciones más practicas para calcular los valores de a y b de la ecuación
aproximada Y = a +b*X son las siguientes:

![]()
Ejemplo:
Sean los valores:
|
x |
3 |
1 |
4 |
6 |
8 |
9 |
11 |
14 |
|
y |
2 |
1 |
4 |
4 |
5 |
7 |
8 |
9 |
a)
Construye el diagrama de puntos
b) Encuentra las
ecuaciones normales
c)
Encuentra la ecuación de la curva de ajuste.
Solución:
a)
Llevando los puntos al sistemas de coordenadas rectangulares.

b) Al observar el
diagrama de puntos, notamos que se aproxima o ajusta a una línea recta, cuya
ecuación es: Y = a+b*X
c)

![]()

Para encontrar
las ecuaciones normales:
![]()
Entonces las ecuaciones normales son:
40 = 8*a +b* 56
364 = 56*a +b*524
Y
= 0.545 + 0.636X
Resolviendo el sistema (Método de Mínimos
Cuadrados) a= 6/11 = 0.545 b=7/11=0.636
d) La ecuación
resultante será :
nota : Si la ecuación es Y = a +b*X
entonces b mide la pendiente de la
línea recta.
![]()
SESION # 15
SEGUNDA
PRACTICA CALIFICADA SESION # 16
5.4 Análisis de
correlación lineal simple:
Definición: Estudia
el grado de asociación que existe entre las variables en estudio, el
coeficiente que mide la mutua asociación se denomina: Coeficiente de
Correlación (r).
Las asociaciones que se pueden presentar son:
1)
Correlación o
asociación Positiva (+), es decir a medidas altas de una variable, le
corresponden medidas altas de otra variable, cambios en el mismo sentido
(Relación Directamente Proporcional)
X ![]() entonces Y
entonces Y ![]()
X ![]() entonces Y
entonces Y ![]()
Ejemplo :
altura y peso
2)
Correlación o
Asociación Negativa (-), En este caso, a valores altos de una variable,
corresponden valores bajos de la otra variable y viceversa. (Relación
inversamente proporcional).
3)
Medidas
no Correlaciónales; No existe ninguna asociación entre las variables.
Características de
Coeficiente de Correlación Lineal Simple
1) r se calcula
mediante la siguiente fórmula:

S (XY)
: covarianza de X e Y
S (X) : desviación
standart de X S (Y) : desviación standart de Y
2)
r es un número abstracto (sin
unidades) y oscila entre –1 y 1, es decir:
![]()
3)
- Si
r es positivo (Correlación
Positiva), entonces las dos características tienden a variar en el mismo sentido.
- Si r es negativo (Correlación Negativa), las dos características
tienden a variar en sentido contrario.
4)
Si r=+1 ó r=-1, entonces la asociación es perfecta.
5)
Si r = 0, no existe asociación entre las variables:
6)
La asociación, tiende a ser más estrecha, cuando r:
![]()
Ejemplo:
(5.4) Calcula
el coeficiente de correlación, del ejemplo (5.1); donde: S(X) =4.06;
S(Y) =2.65;
S(XY)=10.5

Interpretación.- Existe
una alta asociación entre las variables estudiadas. (5.5) del ejemplo (5.2),
donde: S(X)=3.929 pulgadas S(Y)=24.202
libras,
S(XY)=51.370 pulg/lbs

Interpretación.- Existe asociación entre
las alturas y pesos de los estudiantes de la Universidad dada, esta asociación
es directamente proporcional.
5.4 Análisis de Regresión Lineal Simple:
En las relaciones
entre las variables se pueden presentar los siguientes casos:
i)
![]() X influye en Y : X Y
X influye en Y : X Y
![]()
X : variable independiente Y : variable dependiente
Ejemplo:
X = f(Y)![]()
Edad agilidad mental
ii)
![]() Y influye en X Y X Y: variable independiente
Y influye en X Y X Y: variable independiente
X: Variable dependiente
![]() III) Las dos están
influenciadas entre si: X Y
III) Las dos están
influenciadas entre si: X Y
![]() X Y
X Y
Ejemplo : precio y producción de un articulo.
Definición: La regresión permite estudiar
la dependencia de una característica respecto a la otra, para establecer como
varía el promedio de la primera característica al variar la segunda en una
unidad de su medida.
Se
dice regresión lineal, porque las variaciones de la variable independiente,
pueden provocar variaciones proporcionales en las variables dependientes
(ajuste a la línea recta).
Se
dice que la regresión es simple, si una variable independiente influye sobre
otra variable dependiente.
![]()
Ejemplo:
![]() Proteína de harina volumen de pan
Proteína de harina volumen de pan
![]() Ecuación de
Regresión Lineal Simple.
Ecuación de
Regresión Lineal Simple.
 Es una ecuación para estimar una variable dependiente a partir de la
variable independiente.
Es una ecuación para estimar una variable dependiente a partir de la
variable independiente.
Si X : Variable independiente Y : Variable dependiente
![]()
Donde : Y = variable dependiente estimada
: b = coeficiente
de R.L.S.
Características del Coeficiente de R.L.S. (b)
1)
b : indica el número de unidades en que
varía la variable dependiente al variar la independiente en una unidad de su medida.
2)
Si b es positivo los cambios son
directamente proporcionales.
Si b es negativo
entonces los cambios son inversamente proporcional
3)
b : mide la pendiente de la línea de regresión.
4)
b, esta dado en unidades de la variable dependiente.
5)
b y r siempre tienen el mismo signo.
6)
b se calcula:
![]()
![]() Sí Y = f(X), entonces:
Sí Y = f(X), entonces:

Y el valor de la
constante a:
![]()
![]() Si X= f (Y) (se
realiza cambio de X por Y y viceversa)
Si X= f (Y) (se
realiza cambio de X por Y y viceversa)
![]()
![]() Línea de Regresión.- consiste en el trazo
o gráfica de la ecuación de regresión lineal simple, es decir el gráfico de los puntos
Línea de Regresión.- consiste en el trazo
o gráfica de la ecuación de regresión lineal simple, es decir el gráfico de los puntos
si la ecuación es:
Regresión
de Y sobre X; o el gráfico de los puntos
(X,Y) si la ecuación es X= a+ bY
: Regresión de X sobre Y.
Ejemplo:
selecciona al azar
cuatro meses de un
año y se registra tanto los ingresos
como los gastos, en miles de dólares, de cierta empresa:
|
Ingreso (miles de dólares) |
10 |
11 |
12 |
13 |
|
Egresos (miles de dólares) |
4 |
5 |
9 |
10 |
I.
Efectuar un estudio de Regresión Lineal Simple,
asumiendo que los egresos están en función de los Ingresos:
1)
Calculando el coeficiente de Regresión b e interpretándolo
2)
Calculando el coeficiente de intersección a
![]()
3)
Encontrando la ecuación de
Regresión Lineal Simple y trazar la
línea de Regresión.
II.
Realiza un análisis de Correlación Lineal Simple, e
interprete el valor de r.
Solución:
I.
Como el egreso está en función de los ingresos:
Egresos: variable
dependiente: Y
Ingresos: variable
independiente: X
1)
Calculando b
Primero calculamos:
![]()
![]()
Entonces:
![]()
![]()
Interpretación.- Por
cada mil dólares adicional en el Ingreso de dicha empresa, habrá un aumento en
el Egreso de 2.2 miles de dólares en promedio.
2)
![]() Para calcular a :
Para calcular a :
3)
Ecuación de Regresión Lineal Simple:
Como Y es variable
dependiente, entonces:
![]()
Para el trazo en el
sistema de ejes cartesianos se tendrá que reemplazar en la ecuación de
Regresión, los diferentes valores de X:
Y=-18.30 +2.2. (10) =
3.7
Y=-18.30 +2.2
(11) = 5.9
Y=-18.30
+2.2 (12) = 8.1
Y=-18.30 +2.2 (13)
=10.30
También se puede
estimar nuevos valores de los Egresos (Yi) a partir de un valor Xi.
Ejemplo:
Para un ingreso de
15mil dólares, se espera tener en promedio un Egreso de:
Y
=-18.30 + (2.2) (15) = 14.7 miles de dólares La línea de Regresión: unión de
puntos (Xi,Yi)
II.
SO: ESTADISTICA I
![]() Análisis de Correlación:
Análisis de Correlación:
![]()
![]()
Interpretación.- Existe
una alta asociación entre los ingresos y los egresos, siendo los cambios
directamente proporcionales.
![]()
SESION #17
CAPITULO VI: NUMEROS INDICES
Definición.- Un
número índice es una medida estadística diseñada para mostrar los cambios en
una variable (o en un grupo de variables) con respecto al tiempo, situación
geográfica, renta, profesión, etc.
Aplicaciones:
1. Comparar el costo de
alimentos en otros costos de vida durante un año o período con respecto al año
o período anterior.
2. En negocios y Economía.
Tipos de Indice:
(6.1) Indices Simples: Cambios en un
solo bien determinado
1)
Indices de Precios Relativos.- uno de los
ejemplos más sencillos de número índice es un precio relativo, que representa
la razón del precio de un bien determinado en un período con respecto a otro
período llamado base.
Indice de Precio
Relativo: IPR
![]()
Po : precio de un
bien en período base Pn : precio de un bien en período dado
Sí Pa:
precio de un bien en el período a Pb : precio de un bien en el período b
Ejemplo:
(6.1) Supóngase que los precios de consumo de 1 tarro
de leche en junio de 1990 es de 22,000 intis y en junio de 1989 fue de 5,000
intis, tomando 89 como base.
![]() El IPR Simple:
El IPR Simple:
Es
decir: en 1990 el precio de leche fue el 440% del que tenía en el año 89, es
decir se incrementó en un 340%
Observación: IPR Simple es un bien en un
período a (Pa), con respecto al mismo período a (Pa) =1
2)
Indices de Cantidades (o volumen) Relativos.- En lugar de
comparar precios de un bien, se puede también comparar cantidades de un bien
(cantidad de producción, consumo, exportación, etc.) calculemos la cantidad o
volumen relativo (suponiendo que las cantidades dentro de cualquier otro
período son constantes).
Indice de Cantidad
Relativo: IQR
![]()
qn
: cantidad de un bien en el período n
qo : cantidad de un bien en el período base
3)
Valor Relativo.- Si p es precio de un bien durante un período y la
cantidad o volumen producido, vendido, etc., durante ese período.
Valor
total = p * q
Ejemplo:
Si se han vendido
1000 tarros de leche a $0.75 c/u Valor total = 0.75 * 1000 = $ 750
![]()
Si
Po Y qo denotan precio y cantidad de un bien durante un período base y pn y qn
denotan el precio correspondiente durante un período dado, los valores totales
durante estos períodos son Vo y Vn respectivamente y el valor relativo (VR) se define:
![]()
(6.2) Indices Compuestos:
En
la práctica, no se esta tan interesada en comparaciones de precios, cantidades
etc., de bienes individualmente considerados, como en comparaciones de grandes
grupos de tales bienes, es decir es preferible considerar un grupo de bienes
para medir los cambios respectivos.
Los
principales Indices compuestos se calculan teniendo en cuenta los siguientes
métodos:
1)
Método de Agregación Simple.- Este método de cálculo de
un índice de precio (o cantidad), expresa el total de los precios (o cantidades) de bienes en el
período dado, como porcentaje del total de los precios (o cantidades de bienes
en el período base.
Tenemos:
Indice de Precios
de Agregación Simple: IPAS
Donde:
![]() Pn = suma total de precios de bienes empleados en el periodo dado. Po =
suma total de precios de bienes empleados en el año base.
Pn = suma total de precios de bienes empleados en el periodo dado. Po =
suma total de precios de bienes empleados en el año base.
Desventaja: No tiene en cuenta la importancia relativa de las cantidades de los diferentes bienes.
2)
método
de Media de Relativo Simple. En
este método existen varias posibilidades dependiendo del procedimiento empleado
para promediar los precios relativos (o cantidades relativas), tal como la
media aritmética, media geométrica, Mediana,
etc.
Tenemos :
Indice de precios
de Media de Relativo Simple: IPMRS (Promedio de los precios relativos de cada
uno de los bienes empleados):
![]()
Donde:
![]() (Pn/Po) = suma de
los precios relativos de bienes. N =
número total de bienes empleados.
(Pn/Po) = suma de
los precios relativos de bienes. N =
número total de bienes empleados.
![]()
Método de Agregación Ponderada. Para
salvar algún inconveniente del método de agregación simple, se da un peso al
precio de cada bien mediante un factor adecuado, tomando a menudo una cantidad
o volumen del bien determinado durante el periodo dado, o algún periodo típico
(que puede ser una media de varios años). Tales pesos indican la importancia de
cada bien particular.
Aparecen así, los
tres siguientes índices para precios:
(I). Indice de Precios de Laspeyres (o método del
año base): IPL
Pondera los precios considerando como factor de ponderación a las
cantidades en el periodo base.
![]()
Cuando los bienes empleados corresponden a la canasta familiar, el IPL se denomina
índice de Precios del Consumidor o Indice del Costo de Vida, y se utiliza para
medir el nivel de inflación.
(II) Indice de
Precios de Paasche (o método del
año dado): IPP
Pondera los precios de cada bien, considerando como factor de
ponderación a las cantidades del periodo dado.
![]()
(III). Indice Ideal de Fisher
Representa la media geométrica de los índices de Laspeyres y Paasche
(promedio de los índices ponderados).
![]()
Ejemplo:
(6.3) La tabla
muestra los precios y cantidades consumidas de cierto país de distintos
productos férreos en los años 79, 86 y 87.
|
Precios ($/Lbs) |
|||
|
Año |
1979 |
1986 |
1987 |
|
Plata |
17.00 |
26.01 |
27.52 |
|
Cobre |
19.36 |
41.88 |
29.99 |
|
Plomo |
15.18 |
15.81 |
14.46 |
|
Staño |
99.32 |
101.26 |
96.17 |
|
Zinc |
12.15 |
13.49 |
11.40 |
|
Cantidad (Mills de bls) |
|||
|
Año |
1979 |
1986 |
1987 |
|
Plata |
1357 |
3707 |
3698 |
|
Cobre |
2144 |
2734 |
2478 |
|
Plomo |
1916 |
2420 |
2276 |
|
Staño |
161 |
202 |
186 |
|
Zinc |
1872 |
2018 |
1424 |
a)
Calcular Indice de Precios de Agregación Simple para
el año 86, considerando como año base 1979
b)
Calcular el IPL para el año 87, con base en el año 79
c) Calcular el IPP para
el año 87, con año 86
Solución
![]()
Esto
significa, que los precios del conjunto de productos férreos, en el año 86,
representa el 121.7% de los precios que tenían en el año 79, es decir se
incrementaron en 21%.
Nota:
Las
fórmulas descritas anteriormente para obtener números índice de precios se
modifican fácilmente para obtener números índices de cantidad o volumen, con el
simple intercambio de p y q.
![]()
Ejemplo
: Indice de cantidad de Agregación Simple: IQAS
![]()
(6.4) Deflación
Aunque
los ingresos de las personas pueden elevarse teóricamente en un período de dos
años, su ingreso real puede netamente ser inferior, debido al incremento del
costo de vida y por consiguiente su poder de
adquisición.
Ejemplo (5.3)
Si
el ingreso de una persona en 1990 es el 150% de su ingreso en 1989 (es decir a aumentado en 50%)
mientras que el ICV es el 500% del año 89, el salario real de la
persona será en 1990
![]()
El
salario real de la persona en 1990 es el 30% del que tenía en 1989, es decir el
poder adquisitivo de esta persona ha disminuido en 70%.
ANEXOS PROBLEMAS RESUELTOS
a)
tablas de frecuencia y Estadigrafos de posición:
1)
Gramos [10 14.5> [14.5 19.5> [19.5 24.5> [24.5 29.5> hi M/2 0.17 2M M
La siguiente distribución muestra el peso en gramos de 30 paquetes de un
determinado producto:
Se pide completar
la tabla:
Solución
Si la sumatoria de
las hi = 1
Sabemos que : M/2
+ 0.17 +2M +M +0.13 = 1
M/2
+3M = 1-0.30 M/2 +3M = 0.7
![]() 7M = 1.4
7M = 1.4
M = 0.2
sabemos
que
fi = hi * n
Por lo tanto
Remplazando
valores de hi
|
|
|
|
hi |
hi |
|
M/2 |
0.10 |
|
0.17 |
0.17 |
|
2M |
0.40 |
|
M |
0.20 |
|
0.13 |
0.13 |
Completando el
cuadro:
|
Intervalos |
Xi |
fi |
Fi |
hi |
Hi |
|
[10.5 14.5> |
12.25 |
3 |
3 |
0.10 |
0.10 |
|
[14.5 19.5> |
17 |
5 |
5 |
0.17 |
0.17 |
|
[19.5 24.5> |
22 |
12 |
12 |
0.40 |
0.67 |
|
[24.5 29.5> |
27 |
6 |
6 |
0.20 |
0.87 |
|
[29.5 35> |
32.25 |
4 |
4 |
0.13 |
1.00 |
30 1.00
2)Los siguientes datos son los
puntajes obtenidos por 50 estudiantes en un examen de Estadística I:
|
33, |
35, |
35, |
39, |
41, |
41, |
42, |
45, |
47, |
48, |
|
50, |
52, |
53, |
54, |
55, |
55, |
57, |
59, |
60, |
60, |
|
61, |
64, |
65, |
65, |
65, |
66, |
66, |
66, |
67, |
68, |
|
69, |
71, |
73, |
73, |
74, |
74, |
76, |
77, |
77, |
78, |
|
80, |
81, |
84, |
85, |
85, |
88, |
89, |
91, |
94, |
97. |
Clasificar estos
datos convenientemente en intervalos de clase de igual amplitud y construir los
gráficos respectivos.
Solución
I) Rango
= 97-33 = 64
II) K
= 1+3.32 * log (10) = 1+ 3.22 (1.699) = 6.47
CURSO: ESTADISTICA I CICLO
III
![]()
Redondeando
al entero inmediato superior K = 7
(siete intervalos)
III) La amplitud de Clase A
= 64 / 7 = 9.14, aproximando al entero mayor (recuerda que la amplitud debe
tener la característica de los datos)
A = 10
Para facilitar el
conteo de las frecuencias, tomaremos como límite inferior de la primera clase
30.
|
clases |
xi |
fi |
Fi |
hI |
HI |
|
[30, 40> |
35 |
4 |
4 |
0.08 |
0.08 |
|
[40, 50> |
45 |
6 |
10 |
0.12 |
0.20 |
|
[50, 60> |
55 |
8 |
18 |
0.16 |
0.36 |
|
[60,
70 > |
65 |
13 |
31 |
0.26 |
0.62 |
|
[70, 80> |
75 |
9 |
40 |
0.18 |
0.80 |
|
[80, 90> |
85 |
7 |
47 |
0.14 |
0.94 |
|
[90, 100> |
95 |
3 |
50 |
0.06 |
1.00 |
|
TOTAL |
|
50 |
|
1.00 |
|
Nótese que en el
ultimo intervalo el límite superior puede ser abierto ya que sobrepasa al valor
más alto de los datos.
![]() GRAFICOS
GRAFICOS
![]()
2)
El supervisor de una planta de producción desea
comprobar si los pesos netos de las latas de conserva de durazno tienen el peso
reglamentario (18 onzas) para lo cual registra el peso de 36 latas obteniendo
los siguientes datos:
17.0, 17.5,
18.5, 18.1, 17.5,
18.0, 17.5, 17.3,
18.0, 18.0, 18.0,
17.6,
18.2, 17.6, 18.4,
17.7, 17.7, 17.9,
18.3, 17.1, 17.8, 17.3,
18.1,
17.6, 17.7, 18.2, 18.4,
18.0, 18.2, 17.1,
18.6, 18.1, 18.5,
18.4, 17.9, 18.2.
Se pide :
a) Presentar los datos
en una tabla de frecuencia.
b) Determine el peso promedio.
c) Determine el peso
central (la mediana).
d) Determine el peso Modal.
Solución
i) Rango = 18.6 – 17.0 =1.6
ii)
K = 1+ 3.32 * log (36) = 6.17 redondeamos a 6 intervalos
iii)
A = 1.6 / 6 = 0.266 lo aproximamos
a 0.3 (recuerden siempre se redondea
A hacia el mayor respetando la característica de los datos, en este caso con un
digito decimal). A = 0.3
a) La tabla
queda:
![]()
Clase mediana![]()
![]()
b)
onzas
c)
Para la mediana buscar en Fi aquel que sea igual o
mayor que n/2, es decir
![]()
Fi>= 36/2 =18.
![]() Onzas
Onzas
d) Para calcular la
moda usamos el intervalo de mayor fi
![]()
PROBLEMAS PROPUESTOS:
1) La siguiente tabla
muestra las frecuencias relativas de 200 alumnos.
|
EDADES |
16 |
19 |
22 |
25 |
28 |
31 |
|
Hi% |
10 |
15 |
37 |
75 |
85 |
100 |
a) Muestra los límites
de cada intervalo de clase.
b)
Que tanto por ciento de los estudiantes tienen
edades entre 12 y 26 años.
2) Los siguientes datos
son las velocidades en Km./h. De 30 carros que pasaron por un punto de control
de velocidades.
60, 30, 38, 60, 45, 20, 35, 20, 40, 54, 38,
35, 40, 10, 45, 60, 49,
49,
30, 55, 46, 105, 29, 38, 80, 40, 28, 15, 82,
72.
a)
Calcular la media de los datos sin clasificar.
b)
Agrupa estos datos convenientemente.
c) Calcule la media,
mediana y moda.
3)Un grupo de 50
empleados de sistemas de una gran compañía recibe un curso intensivo de
Programación de Ordenadores. De los varios ejercicios distribuidos durante el
curso, se muestra el número de ejercicios completados satisfactoriamente por
los miembros del grupo: 13,
9, 8, 14, 16, 15, 6, 15,
11, 5, 3, 11, 11, 9, 18, 18,
5, 1,15, 12,
16, 12, 14, 9, 6,
10, 5, 12,
17, 11, 12, 13,
8, 19, 12,
11, 18, 15,
13, 9, 10,
9, 10, 7, 21, 16, 12, 9,
2, 13.
a)
Agrupar estas cifras en una tabla de distribución de
frecuencias, usando el método de Sturges.
b)
Calcula la media, mediana y moda.
c)
Estima la desviación típica para datos no agrupados.
4)
Sean los siguientes datos: f1=3, F2=8, F3=18, f5=2, x4=3, K=6,
H4=0.875, A=2, n=24. Completa la tabla de distribución de frecuencias y
calcular la Varianza.
![]() 5)
5)
y dada la siguiente tdf:
|
intervalos |
hi% |
|
[0.5 2.5> |
2% |
|
[2.5 4.5> |
10% |
|
[4.5 6.5> |
h3% |
|
[6.5 8.5> |
16% |
|
[8.5 10.5> |
h5% |
|
[10.5 12.5> |
10% |
|
[12.5 14.5> |
2% |
a) Calcula h3% y h5%
b) Calcula la Varianza.
7) Se tiene una
distribución simétrica de frecuencias con 7
intervalos de igual amplitud A =20 y
considerando los siguientes datos:
X3*f3 = 1260, f2 + f5 = 62, H6% = 96%, f1 =
8, h3% = 21%.
a)
Calcula la media, mediana y moda
b)
Calcula el C.V.
8)
Se conocen los siguientes datos del peso de un grupo
de estudiantes:
Intervalos fi Hi [20 30> [30 40> [40 50> [50 60> 5 0.96 [60 70>![]()
= 50
si
se sabe que: h1=h3 y h2=h4
Determina:
a)
La media, mediana y desviación típica.
b) Presenta los datos
en un Histograma y polígono de frecuencias.
![]()
9) Sabiendo que la
tabla de frecuencias, es simétrica, completarla con los datos, dados, si además
se sabe que la mediana es igual a 27.5.
Luego calcula la media, la moda y la desviación estándar.
|
Intervalo |
Xi |
fi |
Fi |
hi |
Hi |
|
L0 L1 |
|
|
|
|
|
|
L1 L2 |
|
|
|
|
|
|
L2 L3 |
|
|
|
0.20 |
|
|
L3 L4 |
|
|
|
|
0.65 |
|
L4 L5 |
|
|
|
|
|
|
L5 50 |
|
|
|
|
0.95 |
|
50 L7 |
|
|
|
|
|
![]() = 60
= 60
10)
Una fabrica tiene dos departamentos uno de
producción y otro de ventas. Las siguientes tablas de frecuencias presentan los
haberes percibidos hasta fines de abril en cada uno de los departamentos.
![]()
|
Haberes
semanales en dólares |
N°de
trabajadores dpto. de
producción |
|
[10 15> |
15 |
|
[15 20> |
25 |
|
[20 25> |
30 |
|
[25 30> |
20 |
|
[30 35> |
5 |
|
[35 40 |
5 |
|
[40 45 |
0 |
|
Total |
100 |
|
Haberes mensuales en dólares |
N° de trabajadores Dpto. de Ventas |
|
[20 60> |
0 |
|
[60 80> |
5 |
|
[80 100> |
5 |
|
[100 120> |
15 |
|
[120 140> |
20 |
|
[140 160> |
5 |
|
total |
50 |
Calcule:
a) El haber promedio
mensual y la desviación típica correspondiente a cada departamento.
b) El haber promedio
mensual y la desviación típica del conjunto de trabajadores de ambos departamentos.
11)
Se ha recibido una muestra compuesta de 100 probetas
de concreto con el objetivo de analizarlas. Una de las pruebas consistió en
determinar la carga de rotura de dichas probetas, encontrándose los siguientes resultados:
|
Intervalo
de rotura |
N°
de probetas |
|
[120 125> |
10 |
|
[125 130> |
20 |
|
[130 135> |
38 |
|
[135 140> |
25 |
|
[140 145> |
7 |
Determine :
a)
La carga media de
rotura.
b)
La carga mediana de
rotura.
Regresión lineal
1) La tabla muestra
alturas con aproximación de pulgadas y los pesos con aproximación de libras de
una muestra seleccionada al azar:
|
altura |
70 |
63 |
72 |
60 |
66 |
70 |
74 |
65 |
62 |
67 |
65 |
68 |
|
peso |
155 |
150 |
180 |
135 |
156 |
168 |
178 |
160 |
132 |
145 |
139 |
152 |
a)
Hallar la ecuación de la recta de ajuste usando
mínimos cuadrados.
b)
Estimar el peso de un estudiante cuya altura es de
61 pulgadas.
c) Estimar la altura de
un estudiante cuyo peso es de 170 libras.
![]() Solución:
Solución:
|
X |
Y |
|
|
|
X*Y |
|
70 |
155 |
4900 |
|
10850 |
|
|
63 |
150 |
3969 |
9450 |
||
|
72 |
180 |
5184 |
12960 |
||
|
60 |
135 |
3600 |
8100 |
||
|
66 |
156 |
4356 |
10296 |
||
|
70 |
168 |
4900 |
11760 |
||
|
74 |
178 |
5476 |
13172 |
||
|
65 |
160 |
4225 |
10400 |
||
|
62 |
132 |
3844 |
8184 |
||
|
67 |
145 |
4489 |
9715 |
||
|
65 |
139 |
4225 |
9035 |
||
|
68 |
152 |
4624 |
10336 |
||
|
X = 802 |
Y=1850 |
|
X*Y = 124258 |
||
![]()
![]()
![]()
![]() Calculando
a y b:
Calculando
a y b:
![]() a = -60.75
a = -60.75
b = 3.22
![]()
a)
b)Y = -60.75 +
3.22(61) = 135.67 libras. Redondeando Y =136 libras.
c) 170 = -60.75 +
3.22 X
![]() Pulgadas, redondeando X =
72 pulgadas
Pulgadas, redondeando X =
72 pulgadas
2)
La producción de acero en Estados Unidos en millones
de toneladas cortas (una tonelada corta = 2000 libras), durante los años 1946 –
1956 aparecen en la siguiente tabla:
|
Años |
Producción
en Ton. cortas |
|
1946 |
66.6 |
|
1947 |
84.9 |
|
1948 |
88.6 |
|
1949 |
78.0 |
|
1950 |
96.8 |
|
1951 |
105.2 |
|
1952 |
93.2 |
|
1953 |
111.6 |
|
1954 |
88.3 |
|
1955 |
117.0 |
|
1956 |
115.2 |
a)
Halla la ecuación de ajuste (recta de mínimos cuadrados).
b)
Estima la
producción de acero durante los años 1957 y
1958.
c) Estima la producción de acero durante los años 1945
y 1944.
Solución:
Para poder trabajar
con los años se debe colocar una escala paralela que inicie en cero (pues las
fechas no sirven para estos cálculos).
|
Años |
X |
Y |
|
|
|
X * Y |
|
|
||||||
|
1946 |
0 |
66.6 |
0 |
0 |
||
|
1947 |
1 |
84.9 |
1 |
84.9 |
||
|
1948 |
2 |
88.6 |
4 |
177.2 |
||
|
1949 |
3 |
78.0 |
9 |
234.0 |
||
|
1950 |
4 |
96.8 |
16 |
387.2 |
||
|
1951 |
5 |
105.2 |
25 |
526.0 |
||
|
1952 |
6 |
93.2 |
36 |
559.2 |
||
|
1953 |
7 |
111.6 |
49 |
781.2 |
||
|
1954 |
8 |
88.3 |
64 |
706.4 |
||
|
1955 |
9 |
117.0 |
81 |
1053 |
||
|
1956 |
10 |
115.2 |
100 |
1152 |
||
|
TOTALES |
55 |
1045.4 |
385 |
5661.1 |
||
![]() a)
Hallando la recta de ajuste
a)
Hallando la recta de ajuste
![]() a = 75.30
a = 75.30
b = 3.95
![]()
![]()
b y c) Estimando la producción:
|
Años |
X |
Producción |
|
1944 |
-2 |
67.40 |
|
1945 |
-1 |
71.35 |
|
1957 |
11 |
118.75 |
|
1958 |
12 |
122.70 |
PROBLEMAS PROPUESTOS
1)
Construir una línea recta que aproxime los datos de la tabla:
a)
X 2 3 5 7 9 10 Y 1 3 7 11 15 17
estimar los valores de
y para: x= 11, x= 15,
x=4, x= 6
b)
estimar los
valores de
x para:
y= 2, y=5,
2) La producción de acero en Estados Unidos en
millones de toneladas cortas(1 tonelada corta = 2000 libras) durante los años 1986 – 1996 aparece en la tabla:
a) Realiza el diagrama de
dispersión.
b)
Año Producción de acero
en EE.UU.(millones de toneladas cortas) 1986 66.6 1987 84.9 1988 88.6 1989 78.0 1990 96.2 1991 105.2 1992 93.2 1993 111.6 1994 88.3 1995 117.0 1996 115.2
Determina
la ecuación de la recta de ajuste.
c)
Estima la producción de acero
durante los años: 1997 y 1998.
d)
Estima la producción de acero
durante los años: 1985 y1984
e) Halla r e interpreta.
3)
Se desea encontrar una ecuación que estime los
ingresos anuales en función de los salarios mensuales,con este fin se ha
recopilado los salarios mensuales e
ingresos anuales de 8 trabajadores de una
empresa.
|
Salarios mensuales |
100 |
150 |
200 |
275 |
300 |
325 |
350 |
375 |
|
Ingresos anuales |
1200 |
1800 |
2400 |
3300 |
3600 |
3900 |
4200 |
4500 |
a)
![]() Crea el
diagrama de dispersión respectivo.
Crea el
diagrama de dispersión respectivo.
b)
CURSO: ESTADISTICA I CICLO
III
Determina la recta de mínimos cuadrados.
c) Estima los salarios
mensuales para aquellos trabajadores
cuyo ingreso anual es de 5700.
d)
Calcula el coeficiente de Correlación
(interpretar).
![]()
4)
La producción de cigarrillos en Perú durante los
años 1985 –1992 fue:
|
Año |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
|
N°cigarrillos (millones) |
98.2 |
92.3 |
80.0 |
89.1 |
83.5 |
68.9 |
69.2 |
7.1 |
a) Representa el diagrama de dispersión con recta de aproximación.
b)
Halla la ecuación de mínimos cuadrados.
c)
Determina e interpretar el coeficiente de Correlación
d)
Estima la producción de cigarrillos para los años 1995 y 1998.
Números índices
Problemas
propuestos:
1) La siguiente tabla
muestra los precio y cantidades de alguno cereales en los años 1989 y 1998.
![]()
1989
|
producto |
Precio |
Cantidad |
|
Cebada |
1.39 |
237 |
|
Maíz |
1.24 |
3238 |
|
Avena |
0.72 |
1220 |
|
Arroz |
0.086 |
4077 |
|
Centeno |
1.42 |
18.1 |
|
Trigo |
2.24 |
1098 |
1998
|
producto |
Precio |
Cantidad |
|
Cebada |
1.24 |
470 |
|
Maíz |
1.15 |
3800 |
|
Avena |
0.65 |
1422 |
|
Arroz |
0.097 |
4702 |
|
Centeno |
1.27 |
32.5 |
|
Trigo |
2.23 |
1462 |
A)
Tomando como base a 1989 hallar el índice de Laspeyres,
El índice de
Paashe, el índice ideal de Fisher. Para el año 1998.
B)
Tomando como base a 1989 hallar el índice de Laspeyres,
El índice de
Paashe, el índice ideal de Fisher. Para el año 1989.
C) Determine el índice
de agregación simple para los años 1989 y 1998.
2) La tabla muestra los
precios al por menor y producciones medias de antracita y gasolina en EE.UU.
durante los años 1949 y 1958.
precios
|
producto |
1949 |
1958 |
![]()
|
antracita |
$20.13
por
tonelada corta |
28.20
por
tonelada corta |
|
gasolina |
20.3 cent. Por tonelada corta. |
21.4 cent. Por tonelada corta |
cantidades
|
producto |
1949 |
1958 |
|
antracita |
3559 millones de
toneladas cortas |
1821 millones de
toneladas cortas |
|
gasolina |
80.2 millones de barriles * |
118.6 millones de barriles * |
![]() Cada barril
contiene 42 galones.
Cada barril
contiene 42 galones.
a) Determina el índice
de agregación simple para 1958 con base en 1949.
b) Determina el índice
de agregación simple para 1949 con base en 1958.
c) Halla el índice de
Laspeyres, Paashe, Fisher para el año 1958 con respecto a 1949. Interpretar.