Runge-Kutta (RK4) numerical solution for Differential Equations

https://www.intmath.com/differential-equations/12-runge-kutta-rk4-des.php

12. Runge-Kutta (RK4) numerical solution for Differential Equations

In the last section, Euler's Method gave us one possible approach for solving differential equations numerically.
The problem with Euler's Method is that you have to use a small interval size to get a reasonably accurate result. That is, it's not very efficient.
The Runge-Kutta Method produces a better result in fewer steps.

Runge-Kutta Method Order 4 Formula

Applications of RK4

Mechanics

• Springs and dampeners on cars (This spring applet uses RK4.)

Biology

• Predator-prey models
• Fisheries collapses
• Drug delivery
• Epidemic prediction

Physics

• Climate change models
• Ozone protection

Aviation

• On-board computers
• Aerodynamics

$\displaystyle{y}{\left({x}+{h}\right)}$y(x+h) $\displaystyle={y}{\left({x}\right)}+$=y(x)+ $\displaystyle\frac{1}{{6}}{\left({F}_{{1}}+{2}{F}_{{2}}+{2}{F}_{{3}}+{F}_{{4}}\right)}$61​(F1​+2F2​+2F3​+F4​)

where

$\displaystyle{F}_{{1}}={h} f{{\left({x},{y}\right)}}$F1​=hf(x,y)
$\displaystyle{F}_{{2}}={h} f{{\left({x}+\frac{h}{{2}},{y}+\frac{{F}_{{1}}}{{2}}\right)}}$F2​=hf(x+2h​,y+2F1​​)
$\displaystyle{F}_{{3}}={h} f{{\left({x}+\frac{h}{{2}},{y}+\frac{{F}_{{2}}}{{2}}\right)}}$F3​=hf(x+2h​,y+2F2​​)
$\displaystyle{F}_{{4}}={h} f{{\left({x}+{h},{y}+{F}_{{3}}\right)}}$F4​=hf(x+h,y+F3​)

Where does this formula come from?

Here's a brief background to the formula.

Formula derivation

We learned earlier that Taylor's Series gives us a reasonably good approximation to a function, especially if we are near enough to some known starting point, and we take enough terms.
However, one of the drawbacks with Taylor's method is that you need to differentiate your function once for each new term you want to calculate. This can be troublesome for complicated functions, and doesn't work well in computerised modelling.
Carl Runge (pronounced "roonga") and Wilhelm Kutta (pronounced "koota") aimed to provide a method of approximating a function without having to differentiate the original equation.
Their approach was to simulate as many steps of the Taylor's Series method but using evaluation of the original function only.

Runge-Kutta Method of Order 2

We begin with two function evaluations of the form:

$\displaystyle{F}_{{1}}={h} f{{\left({x},{y}\right)}}$F1​=hf(x,y)
$\displaystyle{F}_{{2}}={h} f{{\left({x}+\alpha{h},{y}+\beta{F}_{{1}}\right)}}$F2​=hf(x+αh,y+βF1​)

The $\displaystyle\alpha$α and $\displaystyle\beta$β are unknown quantities. The idea was to take a linear combination of the $\displaystyle{F}_{{1}}$F1​ and $\displaystyle{F}_{{2}}$F2​ terms to obtain an approximation for the $\displaystyle{y}$y value at $\displaystyle{x}={x}_{{0}}+{h}$x=x0​+h, and to find appropriate values of $\displaystyle\alpha$α and $\displaystyle\beta$β.
By comparing the values obtains using Taylor's Series method and the above terms (I will spare you the details here), they obtained the following, which is Runge-Kutta Method of Order 2:

$\displaystyle{y}{\left({x}+{h}\right)}={y}{\left({x}\right)}+\frac{1}{{2}}{\left({F}_{{1}}+{F}_{{2}}\right)}$y(x+h)=y(x)+21​(F1​+F2​)

where

$\displaystyle{F}_{{1}}={h} f{{\left({x},{y}\right)}}$F1​=hf(x,y)
$\displaystyle{F}_{{2}}={h} f{{\left({x}+{h},{y}+{F}_{{1}}\right)}}$F2​=hf(x+h,y+F1​)

Runge-Kutta Method of Order 3

As usual in this work, the more terms we take, the better the solution. In practice, the Order 2 solution is rarely used because it is not very accurate.
A better result is given by the Order 3 method:

$\displaystyle{y}{\left({x}+{h}\right)}=$y(x+h)= $\displaystyle{y}{\left({x}\right)}+\frac{1}{{9}}{\left({2}{F}_{{1}}+{3}{F}_{{2}}+{4}{F}_{{3}}\right)}$y(x)+91​(2F1​+3F2​+4F3​)

where

$\displaystyle{F}_{{1}}={h} f{{\left({x},{y}\right)}}$F1​=hf(x,y)
$\displaystyle{F}_{{2}}={h} f{{\left({x}+\frac{h}{{2}},{y}+\frac{{F}_{{1}}}{{2}}\right)}}$F2​=hf(x+2h​,y+2F1​​)
$\displaystyle{F}_{{3}}={h} f{{\left({x}+\frac{{{3}{h}}}{{4}},{y}+\frac{{{3}{F}_{{2}}}}{{4}}\right)}}$F3​=hf(x+43h​,y+43F2​​)

This was obtained in a similar way to the earlier formula, by comparing Taylor's Series results.
The most commonly used Runge-Kutta formula in use is the Order 4 formula (RK4), as it gives the best trade-off between computational requirements and accuracy.

Get the Daily Math Tweet!
IntMath on Twitter

Let's look at an example to see how it works.

Example

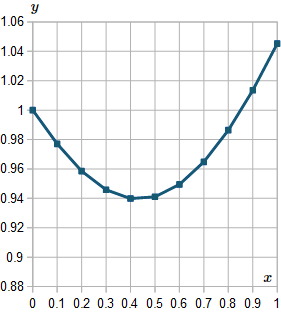
Use Runge-Kutta Method of Order 4 to solve the following, using a step size of $\displaystyle{h}={0.1}$h=0.1 for $\displaystyle{0}\le{x}\le{1}$0≤x≤1.

$\displaystyle\frac{{\left.{d}{y}\right.}}{{\left.{d}{x}\right.}}=\frac{{{5}{x}^{2}-{y}}}{{e}^{{{x}+{y}}}}$dxdy​=ex+y5x2−y​
$\displaystyle{y}{\left({0}\right)}={1}$y(0)=1

Step 1

Note: The following looks tedious, and it is. We'll use a computer (not calculator) to do most of the work for us. The following is here so you can see how the formula is applied.
We start with $\displaystyle{x}={0}$x=0 and $\displaystyle{y}={1}$y=1. We'll find the $\displaystyle{F}$F values first:
$\displaystyle{F}_{{1}}={h} f{{\left({x},{y}\right)}}$F1​=hf(x,y) $\displaystyle={0.1}\frac{{{5}{\left({0}\right)}^{2}-{1}}}{{e}^{{{0}+{1}}}}$=0.1e0+15(0)2−1​ $\displaystyle=-{0.03678794411}$=−0.03678794411
For $\displaystyle{F}_{{2}}$F2​, we need to know:

$\displaystyle{x}+\frac{h}{{2}}={0}+\frac{0.1}{{2}}={0.05}$x+2h​=0+20.1​=0.05, and
$\displaystyle{y}+\frac{{F}_{{1}}}{{2}}$y+2F1​​ $\displaystyle={1}+\frac{{-{0.03678794411}}}{{2}}$=1+2−0.03678794411​ $\displaystyle={0.98160602794}$=0.98160602794

We substitute these into the $\displaystyle{F}_{{2}}$F2​ expression:
$\displaystyle{F}_{{2}}={h} f{{\left({x}+\frac{h}{{2}},{y}+\frac{{F}_{{1}}}{{2}}\right)}}$F2​=hf(x+2h​,y+2F1​​) $\displaystyle={0.1}{\left(\frac{{{5}{\left({0.05}\right)}^{2}-{0.98160602794}}}{{e}^{{{0.05}+{0.98160602794}}}}\right)}$=0.1(e0.05+0.981606027945(0.05)2−0.98160602794​) $\displaystyle=-{0.03454223937}$=−0.03454223937
For $\displaystyle{F}_{{3}}$F3​, we need to know:

$\displaystyle{y}+\frac{{F}_{{2}}}{{2}}$y+2F2​​ $\displaystyle={1}+\frac{{-{0.03454223937}}}{{2}}$=1+2−0.03454223937​ $\displaystyle={0.98272888031}$=0.98272888031

So
$\displaystyle{F}_{{3}}={h} f{{\left({x}+\frac{h}{{2}},{y}+\frac{{F}_{{2}}}{{2}}\right)}}$F3​=hf(x+2h​,y+2F2​​) $\displaystyle={0.1}{\left(\frac{{{5}{\left({0.05}\right)}^{2}-{0.98272888031}}}{{e}^{{{0.05}+{0.98272888031}}}}\right)}$=0.1(e0.05+0.982728880315(0.05)2−0.98272888031​) $\displaystyle=-{0.03454345267}$=−0.03454345267
For $\displaystyle{F}_{{4}}$F4​, we need to know:

$\displaystyle{y}+{F}_{{3}}$y+F3​ $\displaystyle={1}-{0.03454345267}$=1−0.03454345267 $\displaystyle={0.96545654732}$=0.96545654732

So
$\displaystyle{F}_{{4}}={h} f{{\left({x}+{h},{y}+{F}_{{3}}\right)}}$F4​=hf(x+h,y+F3​) $\displaystyle={0.1}{\left(\frac{{{5}{\left({0.1}\right)}^{2}-{0.96545654732}}}{{e}^{{{0.1}+{0.96545654732}}}}\right)}$=0.1(e0.1+0.965456547325(0.1)2−0.96545654732​) $\displaystyle=-{0.03154393258}$=−0.03154393258

Step 2

Next, we take those 4 values and substitute them into the Runge-Kutta RK4 formula:
$\displaystyle{y}{\left({x}+{h}\right)}$y(x+h) $\displaystyle={y}{\left({x}\right)}+\frac{1}{{6}}{\left({F}_{{1}}+{2}{F}_{{2}}+{2}{F}_{{3}}+{F}_{{4}}\right)}$=y(x)+61​(F1​+2F2​+2F3​+F4​)

$\displaystyle={1}+\frac{1}{{6}}{\left(-{0.03678794411}\right.}$=1+61​(−0.03678794411 $\displaystyle-\ {2}\times{0.03454223937}$− 2×0.03454223937 $\displaystyle-\ {2}\times{0.03454345267}$− 2×0.03454345267 $\displaystyle{\left.-\ {0.03154393258}\right)}$− 0.03154393258)

$\displaystyle={0.9655827899}$=0.9655827899
Using this new $\displaystyle{y}$y-value, we would start again, finding the new $\displaystyle{F}_{{1}}$F1​, $\displaystyle{F}_{{2}}$F2​, $\displaystyle{F}_{{3}}$F3​ and $\displaystyle{F}_{{4}}$F4​, and substitute into the Runge-Kutta formula.
We continue with this process, and construct the following table. (I used a spreadsheet to obtain the table. Using calculator is very tedious, and error-prone.)
The table is super wide, so I have put it in the following link:

View table

$\displaystyle{x}$x	$\displaystyle{y}$y	$\displaystyle{F}_{{1}}={h}\frac{{\left.{d}{y}\right.}}{{\left.{d}{x}\right.}}$F1​=hdxdy​	$\displaystyle{x}+\frac{h}{{2}}$x+2h​	$\displaystyle{y}+\frac{{F}_{{1}}}{{2}}$y+2F1​​	$\displaystyle{F}_{{2}}$F2​	$\displaystyle{y}+\frac{{F}_{{2}}}{{2}}$y+2F2​​	$\displaystyle{F}_{{3}}$F3​	$\displaystyle{x}+{h}$x+h	$\displaystyle{y}+{F}_{{3}}$y+F3​	$\displaystyle{F}_{{4}}$F4​
0	1	−0.0367879441	0.05	0.9816060279	−0.0345422394	0.9827288803	−0.0345434527	0.1	0.9654565473	−0.0315439326
0.1	0.9655827899	−0.0315443	0.15	0.9498106398	−0.0278769283	0.9516443257	−0.0278867954	0.2	0.9376959945	−0.023647342
0.2	0.937796275	−0.023648185	0.25	0.9259721824	−0.0189267761	0.9283328869	−0.0189548088	0.3	0.9188414662	−0.0138576597
0.3	0.9189181059	−0.0138588628	0.35	0.9119886745	−0.0084782396	0.9146789861	−0.0085314167	0.4	0.9103866892	−0.0029773028
0.4	0.9104421929	−0.0029786344	0.45	0.9089528756	0.0026604329	0.9117724093	0.002580704	0.5	0.9130228969	0.0082022376
0.5	0.913059839	0.0082010354	0.55	0.9171603567	0.013727301	0.9199234895	0.0136258867	0.6	0.9266857257	0.018973147
0.6	0.9267065986	0.0189722976	0.65	0.9361927474	0.0240794197	0.9387463085	0.0239658709	0.7	0.9506724696	0.0287752146
0.7	0.9506796142	0.0287748718	0.75	0.9650670501	0.0332448616	0.967302045	0.0331305132	0.8	0.9838101274	0.0372312889
0.8	0.9838057659	0.0372315245	0.85	1.0024215282	0.0409408747	1.0042762033	0.0408359751	0.9	1.024641741	0.0441484563
0.9	1.024628046	0.0441492608	0.95	1.0467026764	0.0470593807	1.0481577363	0.0469712279	1	1.0715992739	0.0494916177
1	1.0715783953

I haven't included any values after $\displaystyle{y}$y in the bottom row as we won't be using them.

Easy to understand math videos:
MathTutorDVD.com

Here is the graph of the solutions we found, from $\displaystyle{x}={0}$x=0 to $\displaystyle{x}={1}$x=1.

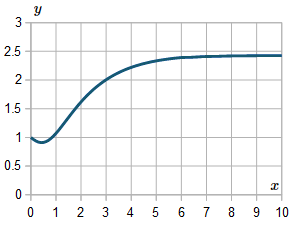
For interest, I extended the result up to $\displaystyle{x}={10}$x=10, and here is the resulting graph:

Exercise

Solve the following using RK4 (Runge-Kutta Method of Order 4) for $\displaystyle{0}\le{x}\le{2}$0≤x≤2. Use a step size of $\displaystyle{h}={0.2}$h=0.2:

$\displaystyle\frac{{\left.{d}{y}\right.}}{{\left.{d}{x}\right.}}={\left({x}+{y}\right)} \sin{{x}}{y}$dxdy​=(x+y)sinxy
$\displaystyle{y}{\left({0}\right)}={5}$y(0)=5

Show answer

Here's the table of values we get. Once again, it's a very wide table so I've put it separately here:

View table

Here is the graph of the solutions we found, from $\displaystyle{x}={0}$x=0 to $\displaystyle{x}={2}$x=2.

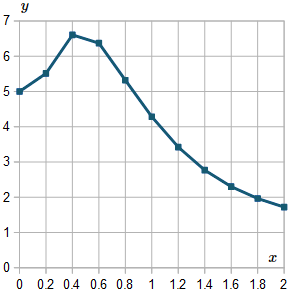
For interest, I extended the result up to $\displaystyle{x}={6}$x=6, and here is the resulting graph:

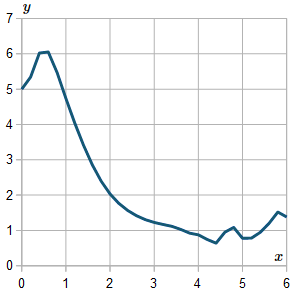
We observe the graph is not very smooth. If we use a smaller $\displaystyle{h}$h value, the curve will generally be smoother.
In fact, this curve is asymptotic to the $\displaystyle{x}$x-axis (it smoothly gets closer to the axis as $\displaystyle{x}$x gets larger). The above graph shows what happens when our intervals are too coarse. (Those wiggles after around $\displaystyle{x}>{4.5}$x>4.5 should not be there.)
Here is the solution graph again, but this time I've used $\displaystyle{h}={0.1}$h=0.1. It's better, but still has a "wiggle" near $\displaystyle{x}={5}$x=5 that should not be there.

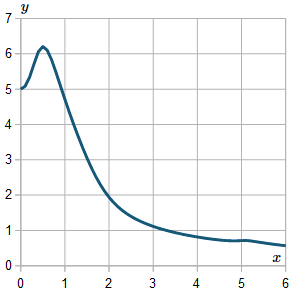
If I took even smaller values of $\displaystyle{h}$h, I'd get a smoother curve. However, that's only up to a point, because rounding errors become significant eventually. Also, computing time goes up for little added benefit.

Improvements to Runge-Kutta

As you can see from the above example, there are points in the curve where the $\displaystyle{y}$y values change relatively quickly (between $\displaystyle{0}$0 and $\displaystyle{1}$1) and other places where the curve is more nearly linear (from $\displaystyle{1}$1 to $\displaystyle{2}$2). Also, we have strange behavior near $\displaystyle{x}={5}$x=5.
In practice, when writing a computer program to perform Runge-Kutta, we allow for variable $\displaystyle{h}$h values - quite small when the curve is changing quickly, and larger $\displaystyle{h}$h values when the curve is relatively smooth.
Mathematics computer algebra systems (like Mathcad, Mathematica and Maple) include routines that calculate RK4 for us, so we just need to provide the function and the interval of interest.

Caution

Always be wary of your answers! Numerical solutions are only ever approximations, and under certain conditions, you can get chaotic results.

IntMath forum

Latest Differential Equations forum posts:

Got questions about this chapter?
Differential equation - has y^2 by Aage [Pending...]
Differential equation by Struggling [Pending...]
dy/dx = xe^(y-2x), form differntial eqaution by grabbitmedia [Solved!]
ODE seperable method by Ahmed [Pending...]
solve the rlc transients AC circuits by Kingston [Solved!]

top

11. Euler's Method - a numerical solution for Differential Equations