Análisis de sonidos de Animales con matlab - Practicas de procesamiento y analisis de señales -

Análisis de sonidos de Animales con matlab - Practicas de procesamiento y analisis de señales - 

https://web.njit.edu/~efortune/n2014/ 

https://web.njit.edu/~efortune/n2014/matoct1.html

https://web.njit.edu/~efortune/n2014/matoct2.html

https://web.njit.edu/~efortune/n2014/matoct3.html

Readings

• An introduction to birdsong and the avian song system
• Aprendiendo neurobiología con los peces eléctricos
• Auditory midbrain neurons that count

##------------------------------------------------------------------------------

##------------------------------------------------------------------------------

%%% Exercise 1: Make a sinewave

% Fs is the sample rate.
% Most audio systems use a sample rate of 44100 Hz.
% The highest frequencies that humans can hear are typically
% in the range of 12000 to 17000 Hz. Here I chose 20 kHz.
% You can change this to see the effect of sample rate.

Fs = 20000;

% The interval intvl is the time for a single cycle at the
% sample rate. For instance, 1 Hz would be 1 second, 2 Hz
% would be 0.5 seconds, 10 Hz would be 0.1 seconds, and 20 Hz
% would be 0.05 seconds.

intvl = 1/Fs;

% Now we will make a time series called tim. You get to
% choose the duration in seconds - here I show 2 seconds (secs. This
% will be the duration of the sinewave.

%% Syntax: There are three parts - a : b : c. a is the time of the first
%% sample. We can't sample at time zero - the first sample
%% will occur at a time determined by the sample rate. b is the
%% interval for every other sample starting after the first.
%% c is the final value, in seconds.

secs = 2;
tim = intvl : intvl : secs;

% Now we make the sinewave using the sin command. You choose
% the frequency freq - which is set
% to 2 Hz here. pi is literally the number Pi (3.1415926...).

freq = 2;
wav = sin(tim*2*pi*freq);

%-- Now we can plot. Figure A:

plot(tim, wav);

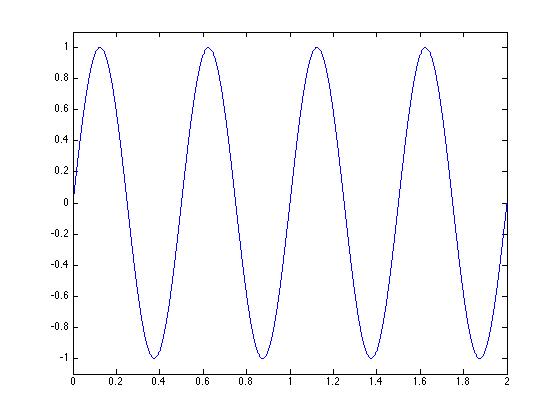
%$ EXERCISE: Learn about the role of sample rate
%$ Try changing the sample rate relative to the frequency.
%$ Here is a suggestion: Fs = 8; freq = 5;
%$ Then you can increase the sample rate to 10, 15, 20, 50, and 100.

%%% Exercise 2: Add two sinewaves

% For this exercise, the two sinewaves need to have the same duration.
% As above, we need a sample rate, and a time sequence.

Fs = 20000;
intvl = 1/Fs;
secs = 2;
tim = intvl : intvl : secs;

% We will make two signals at two different frequencies.
% Each signal can have its own amplitude - basically we can multiply
% by any value we want. Obviously, if we multiply by 0, we will get no
% signal, and 0.5, we'll get 1/2 amplitude. 1 will be the original amplitude.
% In the example here, we have 4 Hz difference in frequencies, and the second signal
% is 1/2 the amplitude of the first.

freq1 = 1000;
freq2 = 1004;

amp1 = 1;
amp2 = 0.5;

% Make the two sinewaves

wave1 = sin(tim*2*pi*freq1) * amp1;
wave2 = sin(tim*2*pi*freq2) * amp2;

% Now add them together and plot the result

addwav = wave1 + wave2;

plot(tim, addwav);

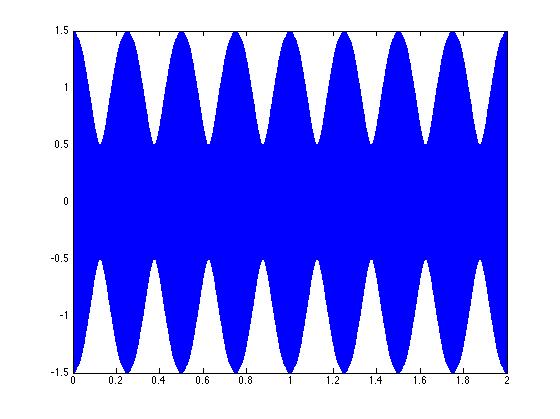
%$ EXERCISE: Learn about interactions between sinewaves
%$ Play around by changing freq2 and amp2.
%$ Try freq2 of 1001, 1002, 1010.
%$ Try amp2 of 1, 0.1, 1.5.
%$ Plot the results using the plot command.
%$ Also plot using the sonogram command.

%%% Exercise 3: Make Sonograms - artificial signal

% We can make a sonogram of any signal to learn more about its spectral and
% temporal characteristics.

% We begin with the signal that we used above, except with different
% frequencies. The frequencies are further apart: freq1 = 1000 and freq2 = 4200.

Fs = 20000;
intvl = 1/Fs;
secs = 2;
tim = intvl : intvl : secs;
freq1 = 1000;
freq2 = 4200;
amp1 = 1;
amp2 = 0.5;
wave1 = sin(tim*2*pi*freq1) * amp1;
wave2 = sin(tim*2*pi*freq2) * amp2;
addwav = wave1 + wave2;

% Now we make a sonogram!
% The critical variable is 'nfft' - this is the length, in samples, over
% which the frequency will be estimate using the Fourier transform. The longer
% the length, the greater precision of the frequency estimate. nfft should always
% be a multiple of 2.

nfft = 256;
specgram(addwav, nfft, Fs);

%- specgram produces a plot

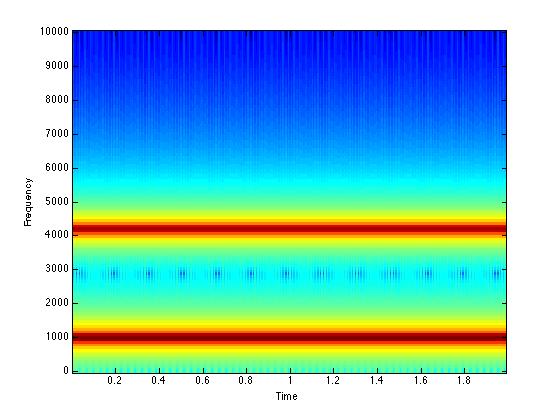
%% Bigger values for nfft lead to better frequency resolution but worse
%% time resolution. Smaller values for nfft have worse frequency
%% resolution but better temporal resolution. The artificial signal
%% we made does not change over time, so we can easily use larger values
%% for nfft.

%$ EXERCISE: Learn about the role of fft window size
%$ Try nfft = 512, 1024, 2048, and 8096 (nfft should be multiples of 2)

%%% Exercise 4: Make Sonograms - natural signal

% We can make a sonogram on any signal.

% Natural signal - we have provided two example bird songs.
% One is a White-crowned sparrow (Zonotrichia leucophrys)
% The other is a Zebra finch (Taeniopygia guttata)

% Load the wav data using the command "wavread"...
% The recording is in xxData, and the sample rate is in xxFs

Get the sound files: wcs.wav zfinch.wav

[ zfData zfFs ] = wavread('zfinch.wav');
[ wcsData wcsFs ] = wavread('wcs.wav');

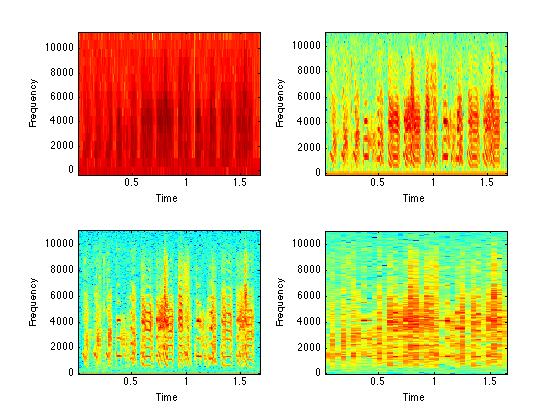
% In this exercise, we will see the effect of the nfft value on the ZF song.

%% A couple of new commands: subplot and specgram...
% subplot(a, b, c); a is number of rows, b is number of columns,
% c tells which panel 1 is top left, 4 is bottom right.

% sonogram(a, b, c, d, e); a is the signal, b is the nfft, c is the
% samplerate, d and e will be explained later - e has a default
% value of 0 and does not need to be typed.

subplot(2,2,1); specgram(zfData, 32, zfFs);
subplot(2,2,2); specgram(zfData, 128, zfFs);
subplot(2,2,3); specgram(zfData, 512, zfFs);
subplot(2,2,4); specgram(zfData, 2048, zfFs);

%$ EXERCISE: Which FFT (nfft) size is best to show the details of
%$ the signal? 32, 128, 512, 2048?? You can try other values - 256 and 1024
%$ are good choices.

% Same for the Sparrow.

% First, make a new figure window using the "figure" command.

figure;

% Plot them!

subplot(2,2,1); specgram(wcsData, 32, wcsFs);
subplot(2,2,2); specgram(wcsData, 128, wcsFs);
subplot(2,2,3); specgram(wcsData, 512, wcsFs);
subplot(2,2,4); specgram(wcsData, 2048, wcsFs);

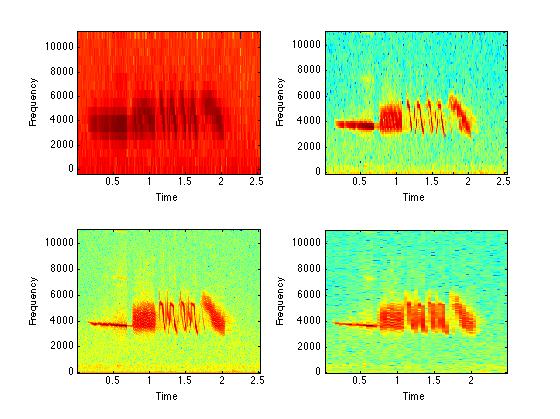
%% For short, variable signals, lower nfft values are most useful.
%% For long, constant signals, higher nfft values are most useful.
%% For wave-type weakly electric fish, which produce constant
%% frequency sinusoidal signals, we sometimes use nfft values
%% of 65536 - which provides very precise frequency resolution.

%% nfft and Fs are related.

%% If Fs is 1000 and nfft is 128, then the sample is 0.128 seconds in duration.
%% If Fs is 10000 and nfft is 128, then the sample is 0.0128 seconds in duration.
%% For the White-Crowned Sparrow, the best nfft window was 512. The song
%% was recorded at a sample rate of 22050 Hz. If the song had been recorded
%% at 44100 Hz, then the nfft window should be 1024.

##------------------------------------------------------------------------------

##------------------------------------------------------------------------------

%%% Exercise 5: Filter a signal

% First let's filter an artificial signal. We'll add two sinewaves together:
% one with a frequency of 5 kHz and the other at 500 Hz. We've done this before,
% so no problem!

freq1 = 5000;
freq2 = 500;

Fs = 20000;
intvl = 1/Fs;
secs = 2;
tim = intvl : intvl : secs;
amp1 = 1;
amp2 = 1;
wave1 = sin(tim*2*pi*freq1) * amp1;
wave2 = sin(tim*2*pi*freq2) * amp2;
addwav = wave1 + wave2;

% We'll do a high-pass and a low-pass filter. We can have different
% frequencies for the high- and low-pass parts, but to start we'll use
% the same frequency, 2500Hz.

lowcut = 2500;
highcut = 2500;

% These next steps make the filter. There are many types of filter -
% the one we are using is called a "Butterworth" filter. The only
% thing to change here is the 'order' - which is the slope of the
% filter. Lower numbers have a broader slope, whereas higher
% numbers have a steeper slope.

order = 5;

lowcut = lowcut*2/Fs;
highcut = highcut*2/Fs;

[b,a] = butter(order,lowcut,'low');
[d,c] = butter(order,highcut,'high');

% Here is where the filtering actually occurs. 'filtfilt' takes the
% filter that we made above, and applies it to the signal, in this case
% addwav.

lowfilt = filtfilt(b,a,addwav);
highfilt = filtfilt(d,c,addwav);

% Now let's plot the results. Top is original signal, middle is high
% pass filtered, bottom is low-pass filtered.

subplot(3,1,1); specgram(addwav, 512, Fs);
subplot(3,1,2); specgram(highfilt, 512, Fs);
subplot(3,1,3); specgram(lowfilt, 512, Fs);

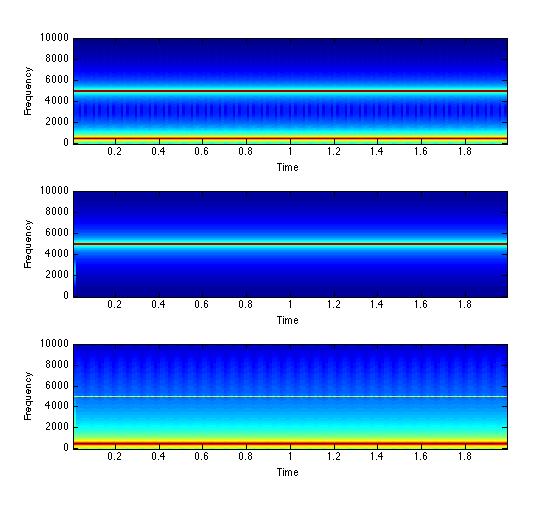
%%% Exercise 6: Filter a signal - noise

% The first step is to make a noisy signal.
% Set the length, in seconds

len = 1;

% Set the SampleRate, in Hz. and make a time series...

Fs = 20000;
tim = 1/Fs:1/Fs:len;

% Make the noise sequence using randn. The arguments are in two
% dimensions… we want a 1 dimensional noisy sequence, hence the
% second dimension is '1'.

noisy=randn(length(tim),1);

% This is great - we can plot this

figure(1);
subplot(3,1,1); specgram(noisy,512,Fs);

% Now we filter, as above, and plot

order = 5;
lowcut = 1500;
highcut = 5700;

lowcut = lowcut*2/Fs;
highcut = highcut*2/Fs;

[b,a] = butter(order,lowcut,'low');
[d,c] = butter(order,highcut,'high');

% Here is where the filtering actually occurs. 'filtfilt' takes the
% filter that we made above, and applies it to the signal, in this case
% addwav.

lowfilt = filtfilt(b,a,noisy);
highfilt = filtfilt(d,c,noisy);

subplot(3,1,2); specgram(highfilt, 512, Fs);
subplot(3,1,3); specgram(lowfilt, 512, Fs);

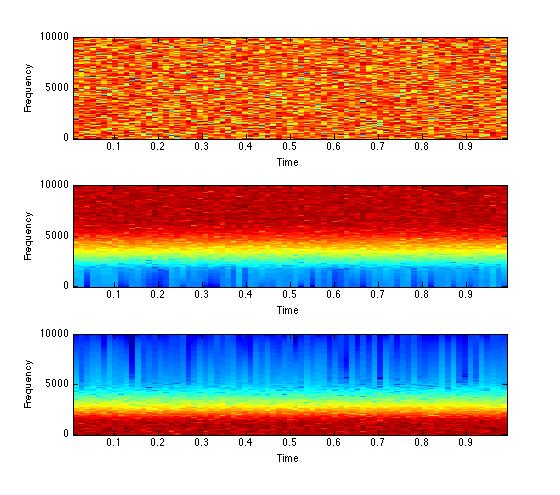
%% Now vary the 'order' of the filter between 1 and 9. What happens?

%% Can you make a bandpass signal, where you filter out signal
%% below 1000 Hz and above 7700 Hz??

%%% Exercise 7: Reverse a signal

% First, we need a signal - let's use the zebra finch song

[ zfData zfFs ] = wavread('zfinch.wav');

% Now we reverse it. "end" is the last value in our variable "zfData". "1"
% is the first value in our variable "zfData". The "-1" in the middle is the
% step size. It defaults to "1" - but we can give it whatever value you want, and
% "-1" means that the steps will go 1 at a time from the end to the first value.

zfRev = zfData(end:-1:1);

% That is all there is to it...

% We can halve the sample rate for both reverse and forward songs...

zfHalfRev = zfData(end:-2:1);
zfHalfData = zfData(1:2:end);

% Let's plot!

figure(1);
subplot(2,1,1);
plot(zfHalfData);
subplot(2,1,2);
plot(zfHalfRev);

%% You can change the sample rate using this technique.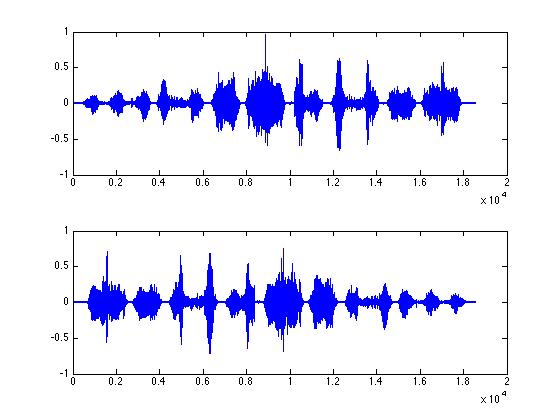

%%% Exercise 8: The "find" command

% The find command is a powerful tool to extract portions of a signal.

% First let's get a signal and plot it:

[ zfData zfFs ] = wavread('zfinch.wav');
tim = 1/zfFs:1/zfFs:length(zfData)/zfFs;

plot(tim,zfData);
% Perhaps we only want to examine the last syllable.
% We can use the "xlim" command to only plot the end.
% In this case we'll plot this syllable that starts at roughly
% 1.3 seconds and ends by 1.7 seconds.

xlim( [ 1.3 1.7 ] );

% There is also a "ylim" command for the y-axis, which does the same thing.

ylim([-0.75 0.75]);

% Now let's use the find command to get the time between 1.45 and 1.63.

pp = find ( tim > 1.45 & tim < 1.63);

% pp is now the sequence of sample positions (not samples!) for which
% tim is larger than 1.45 and smaller than 1.63.

% pp is just sequence of integers.

figure(2); plot(pp);

% But here is how we use pp...

plot( tim(pp), zfData(pp) );

% or better yet...

figure(1); plot( tim, zfData,'b');

hold on; plot( tim(pp) , zfData(pp) ,'r');

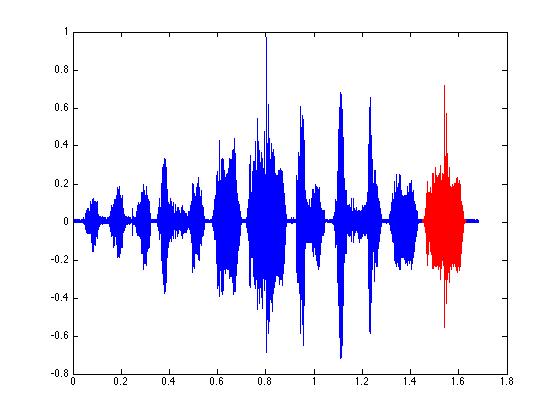
% OK - now another idea. Let's get only the values above a threshold
% Our threshold will be 0.1.

thresh = 0.1;

tt = find ( zfData > thresh );

% Now let's plot it on top of the original signal in red.
% The "hold on" command allows you to plot on the same plot again
% (the default is to erase the old plot and do the new plot).
% You can turn this off using "hold off".

figure(3);
plot(tim, zfData,'b');
hold on;
plot( tim(tt), zfData(tt) ,'r' );
hold off;

##------------------------------------------------------------------------------

##------------------------------------------------------------------------------

%%% Exercise 9: Separate the syllables in a song

% We need to load the data

[ zfData Fs ] = wavread('zfinch.wav');
tim = 1/Fs:1/Fs:length(zfData)/Fs;

% We are going to separate the syllables by amplitude.
% The problem with the original signal is that it goes
% both up and down, so it is not possible to directly
% measure the amplitude. Below I describe two methods,
% "Strategy 1" and "Strategy 2", that can be used to
% make a useful measure of the amplitude.

% These two methods produce nearly the
% same result. The first method is to rectify the
% signal and low-pass filter, and the other
% is to use a function known as "Hilbert" and low-pass
% filter.

% Both require that the signal be centered at zero.
% It is easy to do this by subtracting the mean from
% the original signal.

zfData = zfData - mean(zfData);

%%% Strategy 1: Rectify and smooth

% abs is a function that takes the "absolute value"
% of the signal.

rz = abs( zfData );

% Now we are going to smooth this signal using a filter
% called "medfilt1". Here "sms" is the duration, in
% seconds, of the filter - I have set the default to
% 20 milliseconds. If sms is too long, then it will smooth
% out the signal too much. If sms is too short, then
% you will get spurious syllables.

sms = 0.020;

% we will multiply sms with the sample rate, Fs. This will
% give us the number of samples for the duration that
% sms specifies.

mrz = medfilt1 (rz, Fs*sms);

% We don't need to do the next step, but it makes life
% a little easier later. Here we multiple by 1000 so that
% the values are ~ 1 rather than 0.001.

mrz = mrz * 1000;

%%% Strategy 2: Hilbert and smooth

% This is almost identical to Strategy 1, but uses a
% nice function called Hilbert.

hz = abs( hilbert ( zfData ) );

% Now we do the same filtering as above.

sms = 0.020;
mhz = medfilt1 (hz, Fs*sms);
mhz = mhz * 1000;

%%% Plot

% The original signal

figure(1);
subplot(2,1,1); plot(tim,zfData);

% The same signal after filtering

subplot(2,1,2); plot(tim, mrz, 'r');
hold on; plot(tim, mhz, 'g'); hold off;

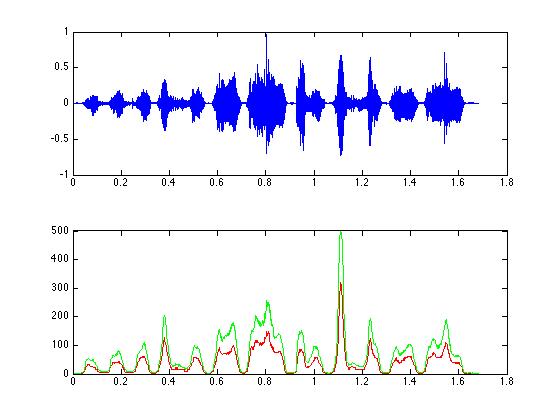
%%% Segment the song into individual syllables

% Animals often produce signals that are composed of multiple
% parts. One strategy to understand the signal is to divide
% it into parts. That is what we will do here - use an
% amplitude threshold to separate each part.

% Now we will replot the same data as in panel 3 of
% of Figure 1, but the y axis will be on a log scale.
% This is acheived using the plotting command "semilogy" which
% plots with the X axis normal and Y axis on a log scale. Yes,
% they also have the command "semilogx".

figure(2);
semilogy(tim, mrz);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% We need to choose a threshold. We can either look at the plot
% and guess, or we can click on the plot and the computer will give
% us the coordinates where we clicked:

% First strategy - I guess "8"!

thresh = 8;

% For clicking, we use the command "ginput". The number is how many
% clicks we are going to make, which is 1 in this case.

thresh = ginput(1);

% If we used ginput, then "thresh" will have two values, % the x value and the y value of the click. We only want the y value, % which is in the second position, and hence we only want
% thresh(2). We can do the following:

thresh = thresh(2);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% Let's replot with a line at the guessed threshold
% just to check. You might have to redo this section
% over and over again with different values for "thresh"
% until we get a value that we think will suffice.

% x will be the first and last sample of the signal.

x(1) = 1;
x(2) = length(tim);

% y will be the amplitude of the threshold

y(1) = thresh;
y(2) = thresh;

% And now we plot the line:

semilogy(tim, mrz, 'b');
hold on;
semilogy(tim(x), y, 'g');
hold off;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

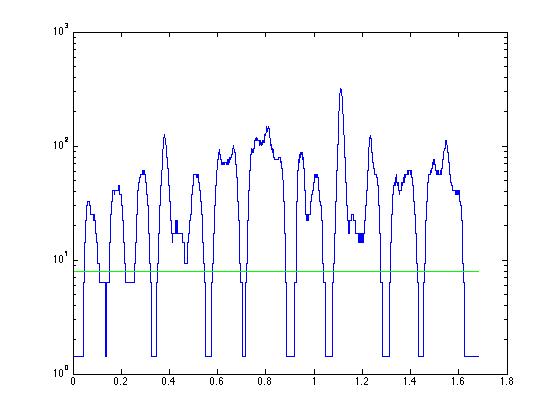
% Now we use the 'find' command to get the part of the
% signal above the threshold. The variable "syls" will % get the index numbers for each value of mrz that is larger % than thresh:

syls = find(mrz > thresh);

% Now we're going to do something that will extract
% the starts and ends of each syllable. This seems
% complicated, but it is simple.

% Make a list of zeros that is the length of the
% signal.

zz = zeros(length(zfData), 1);

% Let's look at zz:

figure(3);

% first replot the original signal.

subplot(3,1,1);
plot(tim, zfData);

% Now plot zz... wow… zeros!

subplot(3,1,2);
plot(tim,zz,'m');

% From above, 'syls' is the list of values that are above
% the threshold - these are where the syllables are located.
% We will set zz to 1 for each of these values...

zz(syls) = 1;

% Now plot this.

hold on;
plot(tim, zz,'r');
hold off;

% Cool - these blocks roughly align with the syllables.
% But what we need are the start times and end times of
% the syllables. We will use a trick to get them...

% 'diff' takes the difference between adjacent values...
% For example sample(2) - sample(1)...

yy = diff(zz);

% Now let's plot this. Starts are marked by '1' and
% ends are marked by '-1'.

subplot(3,1,3);
plot(tim(1:end-1), yy);

% Here we use the find command to get the 'starts' and
% the 'ends'. Notice that we use "==" to indicate when we
% are ASKING if values are equal, but use "=" to SET a variable
% to a value.

starts = find( yy == 1 );
ends = find(yy == -1);

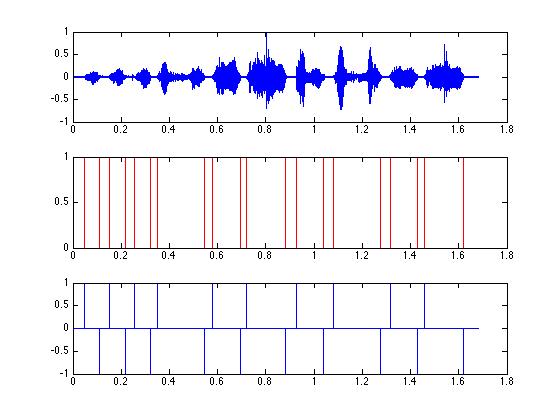
% Now this is simple! We use a loop - the 'for' command
% to get each syllable. The only part that you haven't
% seen earlier is the '{}' - called 'curly brackets'.
% syllable{1} will have the entire 1st syllable, and
% syllable{2} will have the enture 2nd syllable, etc.

% timmy and timm are not necessary, but might be useful.
% timmy is the real times from the song.
% timm is a time sequence for each syllable only.

for i = 1:length(starts)
syllable{i} = zfData(starts(i):ends(i));

timmy{i} = tim(starts(i):ends(i));
timm{i} = 1/Fs:1/Fs:(1 + ends(i) - starts(i))/Fs;

end;

% Just to show what has happened, here is a plot:
% I picked syllables 4,5,6, and 7. You can pick others
% if you wish.

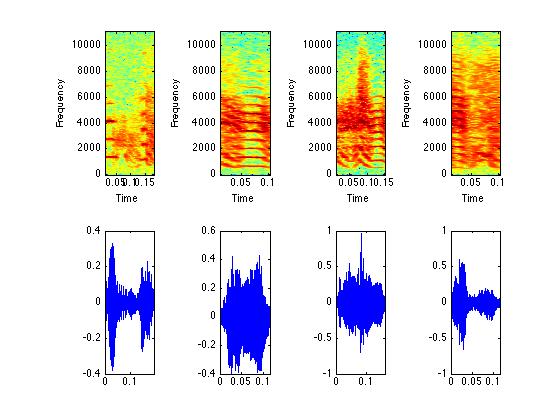
figure(4);
subplot(2,4,1); specgram(syllable{4},512,Fs,[],500);
subplot(2,4,2); specgram(syllable{5},512,Fs,[],500);
subplot(2,4,3); specgram(syllable{6},512,Fs,[],500);
subplot(2,4,4); specgram(syllable{7},512,Fs,[],500);

subplot(2,4,5); plot(timm{4},syllable{4}); xlim([0 timm{4}(end)]);
subplot(2,4,6); plot(timm{5},syllable{5}); xlim([0 timm{5}(end)]);
subplot(2,4,7); plot(timm{6},syllable{6}); xlim([0 timm{6}(end)]);
subplot(2,4,8); plot(timm{7},syllable{7}); xlim([0 timm{7}(end)]);

% Now we will get the silent parts between syllables.
% This can be important because sometimes the time
% between signals is an independent signal. For example,
% in frogs the duration between calls determines the
% "pulse repetition rate", which can indicate whether
% the call is a mate attraction signal or an aggressive
% signal.

% The procedure is almost the same as for the
% syllables as above. What is different is that instead
% of copying the signal from zfData, we instead make
% pure silence by putting in a flat signal with an
% amplitude of 0.

% We use a loop for each of the ends (which is the start of each silence)
% Make a list of zeros with the length of the interval
% We get the length of the interval by getting the difference
% between the end of the silence, which is the 'start' of
% the next syllable, and the start of the silence, which is
% the 'end' of the previous syllable. Complicated!?!?

for j = 2:length(ends);
nop{j} = zeros( (starts(j)-ends(j-1)), 1);

% This next step is not necessary - just a time base for the silence.

noptimmy{j} = tim(ends(j-1):starts(j));
end;

% For review: you can easily get the data for each
% syllable.
% syllable{1} is the data for the first syllable,
% and syllable{2} the second.

% Let's plot a syllable.

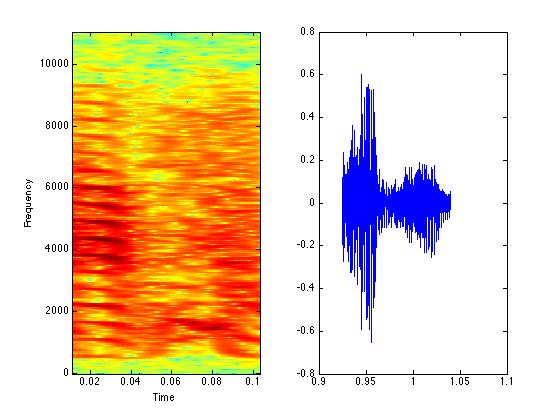
figure(1);
subplot(1,2,1);
specgram(syllable{7},512,Fs,512,500);
subplot(1,2,2);
plot(timmy{7},syllable{7});

% How many syllables did we find??

length(syllable)

% How long (duration) is syllable{7}?

length(syllable{7})/Fs

%%% Exercise 10: Make a NEW song with the syllable order reversed

% Here we are going to take each syllable, and instead
% of the normal order of ABCDEFG we will make the order
% GFEDCBA. Easy!

% Here we are making a new variable, 'revordersong' and
% we are putting the last syllable in there.
% The apostrophe - ' - changes the data from rows to columns
% or from columns to rows. In this case the data in
% 'syllable' is a column, and to concatenate them, we need
% the data to be in a row. Why this is, I don't know.

revordersong = syllable{end}';

% Now we will cycle though each syllable from the second
% to last to the first (we already have the last syllable
% from the above line.

% The variables in the brackets will be concatenated.
% so [ revordersong nop syllable ] will make
% the previously defined revordersong followed by the
% silent period, which is then followed by the next
% syllable. Recall that the apostrophe makes the
% data into a single row.

for k = length(syllable)-1:-1:1;
revordersong = [revordersong nop{k+1}' syllable{k}'];
end;

% This is nice to add - a time base for this new signal.
% We've seen this many times by now.

revtim = 1/Fs:1/Fs:length(revordersong)/Fs;

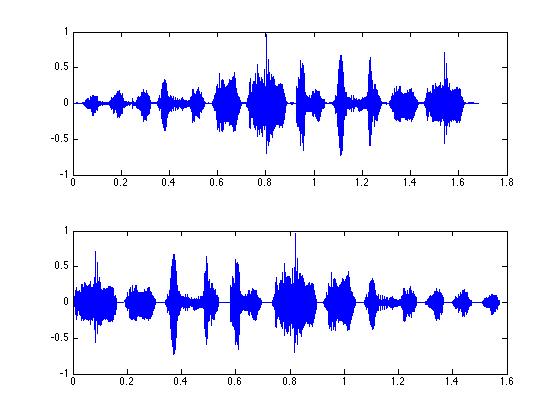
% now let's plot it:

subplot(2,1,1); plot(tim,zfData);

% And the reversed signal below:

subplot(2,1,2); plot(revtim, revordersong);

% or we can show the spectra...

%original signal

subplot(2,1,1); specgram(zfData,512,Fs);

% reversed signal

subplot(2,1,2); specgram(revordersong,512,Fs);

% Save the data to a wave file. You can then use
% Windows to listen to it.

wavwrite(revordersong', Fs, 16, 'revordersong.wav');

%%% Exercise 11: Make a NEW song with each syllable reversed, but the syllable order normal

% This is nearly identical to the previous exercise,
% but now the order is correct (ABCDEF) but each syllable
% is reversed.

% Take the first syllable and put it in our new variable
% revsylsong...

revsylsong = syllable{1}';

% Now reverse it - we saw how to do this in an earlier
% exercise...

revsylsong = revsylsong(end:-1:1);

% Now do the same for the rest of the syllables, adding them
% to the new variable...

% We are using a temporary variable 'ra' to do the reversing

for l = 2:length(syllable);
ra = syllable{l}';
revsylsong = [revsylsong nop{l}' ra(end:-1:1)];
end;

% and of course, the time data...

revsyltim = 1/Fs:1/Fs:length(revsylsong)/Fs;

% Cool. Now let's do the same plots...

figure(6);

% The original signal above:

subplot(2,1,1); plot(tim,zfData);

% The reversed signal below:

subplot(2,1,2); plot(revsyltim, revsylsong);

% or we can show the spectrum...

% original signal

subplot(2,1,1); specgram(zfData,512,Fs);

% reversed signal

subplot(2,1,2); specgram(revsylsong,512,Fs);

% and save to a file that we can play on the
% computer:

wavwrite(revsylsong', Fs, 16, 'revsylsong.wav');

% You can see that with these tools you can make
% a very wide range of arbitrary stimuli from
% your recordings of animal signals. These are
% powerful tools for sensory electrophysiology.

% Try to do the same exercises with the data in
% wcs.wav.

%%% Exercise 12: Spikes

% In this exercise we will take a recording of neural activity (spikes!) and
% turn them into data that we can start to analyze in useful ways.

% I have provided two sample files will nice recordings of neural activity.
% They are very different from each other.

% Read the first file, make the time data, and plot.(easy easy by now)

[a Fs] = wavread('spikes1.wav' );
tim = 1/Fs:1/Fs:length(a)/Fs;
figure(7);
plot(tim,a);

% And you can do a close up of one second of data...

xlim([3 4]);

% Now we want to set an amplitude threshold for the spikes.
% Different recordings will have different amplitudes
% for spikes.
% Here I have guessed that 0.5 will be sufficient. Look
% at the plot to confirm.

thresh = 0.5;

% We use the find command to get all of
% the data above threshold.

spikes = find( a > thresh );

% This is a complicated, but necessary step. Spikes are
% more than 1 or two milliseconds in duration. Thus, we
% want a threshold
% for the interval between spikes - anything less than
% that threshold is a mistake from the find command.

% Our threshold will be 1 millisecond: 0.001 seconds.
% Since are data is in samples and not in milliseconds, we'll
% set our threshold to the sample rate * milliseconds.

% 'diff' is the difference between adjacent data points.
% So, here we find all of the instances where the number of
% samples between spikes is greater than our threshold of
% 1 millisecond samples (which for Fs = 10000 is 10 samples).

spikes1 = spikes( find( diff(spikes) > 0.001*Fs));

% How many spikes did we find?

length(spikes1)

% What is the spike rate??

length(spikes1) / tim(end)

% Now let's plot. We'll plot a STAR at each time
% that a spike occurred. The 'ones' command is
% identical to the zeros command, except that each
% value is one. This would be OK, but I decided to
% multiply it by the threshold so that the dots
% will be at the level of the threshold when we
% plot it. you will see...

ys = ones(length(spikes1),1) * thresh;

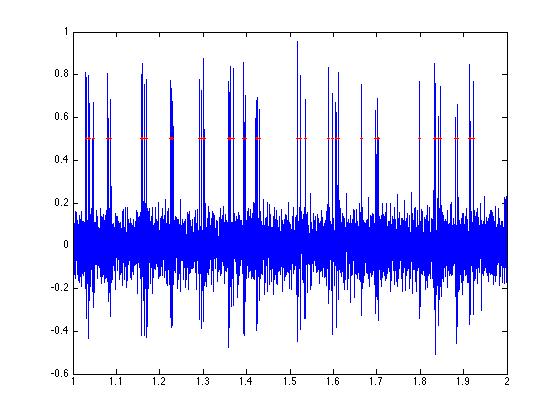
% Now plot...

plot(tim,a,'b');
% Markersize changes the size of the symbols.

% Try the same plot with 1 or 3 or 4 to see
% what happens to the plot.

hold on; plot(tim(spikes1),ys,'r*','markersize', 2);
hold off;

% Now zoom in!

xlim([1 2]);

% even further...

xlim([1 1.25]);

% Another important measure is the time between spikes
% This is very easy to get using the 'diff' command.
% diff will give use the number of samples between
% spikes, and then we divide by the sample rate to
% get the time, in seconds, between spikes.

intervals1 = diff(spikes1)/Fs;

% Here are some easy measurements...

mean(intervals1)
max(intervals1)
min(intervals1)

% But looking at the plot, we see that the spikes
% are in "bursts" rather than randomly spread.
% If they were randomly timed, we would find a
% random distribution of the intervals between
% spikes. Let's take a look using a histogram...

hist(intervals1,100);

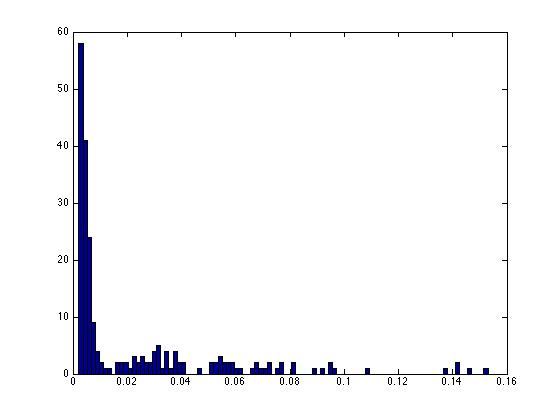
% For these data we see that there are many many
% intervals below 0.015 (15 milliseconds), and a
% spread of longer intervals.
% This plot is a very good example of a "bursty" neuron.

% The other data, spikes2.wav, is very very different.

% Please do the same analysis for those data as you
% did for spikes1.wav. Use different variable names
% like changing spikes1 to spikes2 and interval1 to
% interval2. so that you can make the following plots...

% Data from spikes1,wav
subplot(2,1,1);
hist(intervals1,100);

% Data from spikes2.wav
subplot(2,1,2)
hist(intervals2,100);