Teorema del coseno o de los cosenos
Contenido de esta página:
Introducción
Teorema del coseno (enunciado y demostración)
6 Problemas resueltos de aplicación del teorema del coseno
1. Introducción
El teorema del coseno (o teorema de los cosenos) es un resultado de trigonometría que establece la relación de proporcionalidad existente entre las longitudes de lados de un triángulo cualquiera con los cosenos de sus ángulos interiores opuestos. Este teorema es una generalización del teorema de Pitágoras (la razón de ello se encuentra en la nota del siguiente apartado).
Para aplicar el teorema del coseno se necesita conocer la longitud de dos lados y la medida de un ángulo interior (opuesto al del otro lado).
En esta página enunciamos y demostramos el teorema del coseno y resolvemos problemas de su aplicación en los que se pregunta por algún lado o ángulo de un triángulo dado. En algunos de los problemas se necesitan otros resultados básicos como el teorema de Pitágoras y la propiedad de que la suma de los ángulos internos de un triángulo es 180º.
2. Teorema del coseno
Sea un triángulo cualquiera con lados , y y con ángulos interiores , y (son los ángulos opuestos a los lados, respectivamente).
Entonces, se cumplen las relaciones
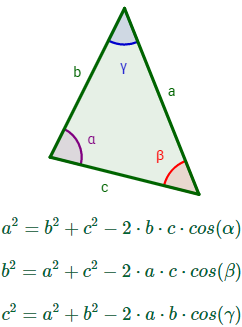
Nota: se dice que es una generalización de Pitágoras porque si uno de los ángulos es recto, el triángulo es rectángulo, siendo la hipotenusa el lado opuesto a dicho ángulo y se obtiene el teorema de Pitágoras al aplicar el del coseno.
Por ejemplo, si α = 90º, entonces, la primera de las tres fórmulas anteriores queda como
siendo a la hipotenusa del triángulo.
Haremos la demostración por el teorema de Pitágoras, pero demostraremos únicamente la fórmula
para el caso en el que el lado b es adyacente a dos ángulos agudos (como en la imagen siguiente). En los otros casos, se procede de forma similar.
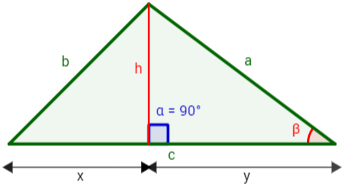
Hemos dividido el triángulo en dos triángulos rectángulos. Observemos que el lado c es
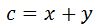
de donde
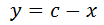
Aplicando el teorema de Pitágoras al triángulo de la izquierda, obtenemos la relación
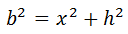
y aplicando Pitágoras al triángulo de la derecha,
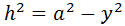
Escribimos en esta última relación y como c - x:
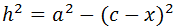
Sumamos las dos relaciones obtenidas:
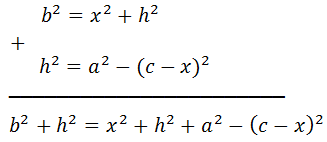
Simplificamos la expresión:
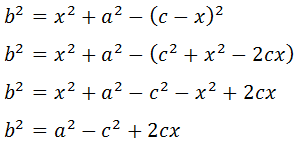
Finalmente, puesto que el triángulo de la derecha es rectángulo, por definición del coseno,
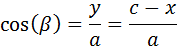
Despejamos x:
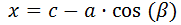
Sustituimos esta x en la expresión que teníamos:
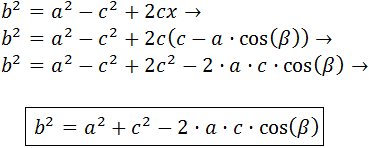
No hay comentarios:
Publicar un comentario