Sistema cartesiano - Coordenadas cartesianas

https://e1.portalacademico.cch.unam.mx/alumno/matematicas1/unidad2/sistemaCartesiano/sistemaCartesiano

Sistema cartesiano

Según los historiadores, el sistema cartesiano fue inventado por el filósofo y matemático francés René Descartes (1596-1650) quien, desde muy pequeño, quedó huérfano y padecía problemas de salud; esta condición lo obligaba a pasar mucho tiempo en la cama, lo cual le permitía pensar, leer, estudiar y escribir. Un día, estando en la cama de su habitación, observó a una mosca parada en el techo, cerca de la esquina de dos paredes adyacentes, y se preguntó si podía conocer su posición en cada instante; después de pensar, reflexionar y analizar, se le ocurrió lo que hoy conocemos como sistema cartesiano, lo cual permitiría representar la posición exacta de la mosca en cualquier momento.

El sistema cartesiano de René Descartes contribuyó al desarrollo de la matemática moderna al vincular el Álgebra y la Geometría, dando como resultado la Geometría Analítica, mediante la cual se grafican figuras geométricas, se analizan sus propiedades para la formulación de expresiones matemáticas, en particular, para la graficación de aquellas que involucran variación directamente proporcional. Para comprender mejor todo esto, a continuación se describen las características y propiedades del sistema cartesiano.

El sistema cartesiano está formado por dos rectas que se cortan perpendicularmente y que dividen al espacio bidimensional en cuatro cuadrantes. La recta horizontal se le conoce como el eje de las abscisas Eje x$x$, mientras que la recta vertical se le llama el eje de las ordenadas Eje y$y$. Los elementos del sistema cartesiano son las parejas ordenadas (x,y)$(x,y)$, en éstas, la primera coordenada corresponde al Eje x$x$, y la segunda coordenada corresponde al Eje y$y$. Las coordenadas del punto P$P$ ilustran las parejas ordenadas, puede presentarse la situación en que alguna de las coordenadas coincida con alguno de los ejes coordenados, en este caso las coordenadas son P(x,0)$P(x,0)$ o P(0,y)$P(0,y)$ cuando el punto coincida con el Eje x$x$ o el Eje y$y$, respectivamente.

 A continuación, en el recurso GeoGebra explorarás los signos de las coordenadas del punto P(x,y)$P(x,y)$ en el plano cartesiano, para ello da clic en Exploración de los signos y sigue las instrucciones. Al terminar responde las siguientes preguntas y da clic en Verificar para recibir retroalimentación.

1. ¿Cuáles son los signos de las coordenadas del primer cuadrante? ($($
    
    , 
    )$)$
2. ¿Cuáles son los signos de las coordenadas del segundo cuadrante? ($($
    
    , 
    )$)$
3. ¿Cuáles son los signos de las coordenadas del tercer cuadrante? ($($
    
    , 
    )$)$
4. ¿Cuáles son los signos de las coordenadas del cuarto cuadrante? ($($
    
    , 
    )$)$

Con base en las actividades que realizaste se concluye que:

•  Las coordenadas de los puntos en el primer cuadrante son positivas.
•  En el segundo las abscisas son negativas y las ordenadas positivas.
•  En el tercer cuadrante ambas coordenadas son negativas.
•  En el cuarto cuadrante las abscisas son positivas y las ordenadas negativas.

Esto te facilitará la graficación de figuras geométricas en el plano cartesiano.

Practicando

Observa la siguiente figura geométrica, ésta se construyó con la unión de las coordenadas de los puntos que se especifican en los cuadrantes del sistema cartesiano. Escribe en la tabla las coordenadas de los puntos A, R, P, I y D. al finalizar da clic en Verificar para recibir retroalimentación.

Puntos	A	R	P	I	D
Coordenadas	($($    ,   )$)$	($($    ,   )$)$	($($    ,   )$)$	($($    ,   )$)$	($($    ,   )$)$

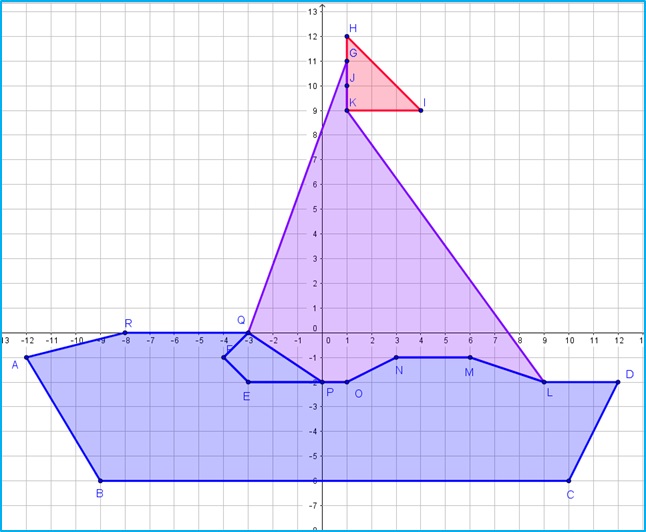
Como puedes observar, el punto A se encuentra en el tercer cuadrante por tener sus coordenadas negativas, el punto R se encuentra sobre el Eje x$x$ puesto que su ordenada es cero, el punto P se encuentra sobre el Eje y$y$ por tener abscisa cero, el punto I se localiza en el primer cuadrante por tener coordenadas positivas y el punto D se ubica en el cuarto cuadrante por tener abscisa positiva y ordenada negativa.