Golden Number, angle 36, cos(36°)=(1+√5)/4=Phi/2=GoldenNumber/2

Golden Number, angle 36, cos(36°)=(1+√5)/4=Phi/2=GoldenNumber/2

https://www.cut-the-knot.org/pythagoras/cos36.shtml 

cos 36°

The purpose of this page is to establish that

cos(36∘)=(1+5–√)4.

It's a good exercise in trigonometry that was also useful in solving a curious sangaku problem.

We start with a regular pentagon. As every regular polygon, this one too is cyclic. So that we may assume its vertices lie on a circle and sides and diagonals form inscribed angles.

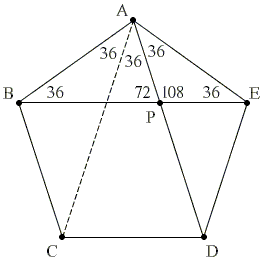
It follows that every angle of the regular pentagon equals 108∘. Inscribed ∠CAD is half of the central angle 72∘=360∘5, i.e.

∠CAD=36∘.

By symmetry ∠BAC=∠DAE implying that these two are also 36∘. (Note in passing that we just proved that angle 108∘ is trisectable.) Other angles designated in the diagram are also easily calculated.

As far as linear segments are concerned, we may observe that triangles ABP, ABE, AEP are isosceles, in particular,

AB=BP,
AB=AE,
AP=EP.

Triangles ABE and AEP are also similar, in particular

BE/AB=AE/EP, or
BE×EP=AB2, i.e.
(BP+EP)×EP=AB2, and lastly,
(AB+EP)×EP=AB2.

For the ratio x=AB/EP we have the equation

x+1=x2,

with one positive solution x=ϕ, the golden ratio. (These calculations were in fact performed to justify a construction of regular pentagon. We return to them here in order to facilitate the references.)

In △AEP, AE=AB and EP is one of the sides such that AE/EP=ϕ. Drop a perpendicular from P to AE to obtain two right triangles. Then say,

cos(∠AEP)=(AE/2)/EP=(AE/EP)/2=ϕ/2.

But ∠AEP=36∘ and we get the desired result.

Using cos(36∘)=(1+5–√)/4 we can find

cos(18∘)=2(5+5–√)−−−−−−−−√/4

from cos2α=2cos2α−1 and then

sin(18∘)=2(3−5–√)−−−−−−−−√/4

from cos2α+sin2α=1. Now, it may be hard to believe but this expression simplifies to

sin(18∘)=(5–√−1)/4,

which is immediately verified by squaring the two expressions. Also

sin(36∘)=2(5−5–√)−−−−−−−−√/4

from sin2α=2 sinα cosα.

We can easily find cos(72∘) from cos2α=2cos2α−1:

cos(72∘)

This is of course equal to sin(18∘) as might have been expected from the general formula, sinα=cos(90∘−α).

And, of course,

sin(72∘)=2(5+5–√)−−−−−−−−√/4

because sin(72∘)=cos(18∘).

Finally, let's compute sin54∘:

sin54∘

as expected since sin54∘=cos36∘.

Trigonometry

• What Is Trigonometry?
• Addition and Subtraction Formulas for Sine and Cosine
  • Sine of a Sum Formula
  • Addition and Subtraction Formulas for Sine and Cosine II
  • Addition and Subtraction Formulas for Sine and Cosine III
  • Addition and Subtraction Formulas for Sine and Cosine IV
  • Addition and Subtraction Formulas
• The Law of Cosines (Cosine Rule)
• Cosine of 36 degrees
• Tangent of 22.5o - Proof Wthout Words
• Sine and Cosine of 15 Degrees Angle
• Sine, Cosine, and Ptolemy's Theorem
• arctan(1) + arctan(2) + arctan(3) = π
• Trigonometry by Watching
• arctan(1/2) + arctan(1/3) = arctan(1)
• Morley's Miracle
• Napoleon's Theorem
• A Trigonometric Solution to a Difficult Sangaku Problem
• Trigonometric Form of Complex Numbers
• Derivatives of Sine and Cosine
• ΔABC is right iff sin²A + sin²B + sin²C = 2
• Advanced Identities
• Hunting Right Angles
• Point on Bisector in Right Angle
• Trigonometric Identities with Arctangents
• The Concurrency of the Altitudes in a Triangle - Trigonometric Proof
• Butterfly Trigonometry
• Binet's Formula with Cosines
• Another Face and Proof of a Trigonometric Identity
• cos/sin inequality
• On the Intersection of kx and |sin(x)|
• Cevians And Semicircles
• Double and Half Angle Formulas
• A Nice Trig Formula
• Another Golden Ratio in Semicircle
• Leo Giugiuc's Trigonometric Lemma
• Another Property of Points on Incircle
• Much from Little
• The Law of Cosines and the Law of Sines Are Equivalent
• Wonderful Trigonometry In Equilateral Triangle
• A Trigonometric Observation in Right Triangle
• A Quick Proof of cos(pi/7)cos(2.pi/7)cos(3.pi/7)=1/8

Fibonacci Numbers

1. Ceva's Theorem: A Matter of Appreciation
2. When the Counting Gets Tough, the Tough Count on Mathematics
3. I. Sharygin's Problem of Criminal Ministers
4. Single Pile Games
5. Take-Away Games
6. Number 8 Is Interesting
7. Curry's Paradox
8. A Problem in Checker-Jumping
   • Getting a Scout out of Desert
9. Fibonacci's Quickies
10. Fibonacci Numbers in Equilateral Triangle
11. Binet's Formula by Inducion
12. Binet's Formula via Generating Functions
13. Generating Functions from Recurrences
14. Cassini's Identity
15. Fibonacci Idendtities with Matrices
16. GCD of Fibonacci Numbers
17. Binet's Formula with Cosines
18. Lame's Theorem - First Application of Fibonacci Numbers

• Golden Ratio in Geometry