Metodo de Bairstow Leave a comment
Explicación del Método
En análisis numérico, el método de Bairstow es un algoritmo eficiente de búsqueda de las raíces de un polinomio real de grado arbitrario.El
algoritmo apareció por primera vez en el apéndice del libro
“Aerodinámica Aplicada”, escrito por Leonard Bairstow y publicado
en1920. El algoritmo se diferencia de otros métodos en que encuentra
tanto las raíces reales como las imaginarias (en parejas complejas
conjugadas), utilizando únicamente aritmética real.
El método de BAIRSTOW, Es un método
iterativo relacionado con los métodos de Müller y Newton Raphson. El
método consiste en el cálculo de las raíces de un polinomio buscando
factores cuadráticos x^2-rx-s del mismo, es decir, tales que:

Evidentemente, si x^2-rx-s no es un factor cuadrático de p(x) se tendrá:
Tomando el polinomio en orden descendente y los coeficientes del mismo en orden ascendente:
Si en términos generales se tiene un polinomio descrito de la forma:
Y para efectos del ejemplo se tiene:
Si se asume como valor inicial para r=1 y s=1, se tiene que el polinomio factor cuadrático será:
Si se divide entre pc dará como resultado p1(x) y residuo Ax+B.
De manera general se puede bosquejar así:
Donde Ax+B es el residuo de la división.
Siendo A y B funciones de r y de s, de forma que el método consiste en
encontrar los valores de r y s que hacen:
Para ello se aplica el método de newton
Raphson en la forma conocida, lo que conlleva la evaluación de la matriz
jacobiana del sistema anterior, así como de las funciones A y B, en
cada iteración. Un modo de realizar estas evaluaciones, ya que la forma
explícita de las funciones A(r,s) y B(r,s) no es conocida
explícitamente, es construir el siguiente algoritmo:
Y encontrar los valores de A, B, A1 y B1
mediante el proceso similar al de Hörner siguiente que se obtiene al
desarrollar los productos e identificar los coeficientes:
Sean:
Sean:
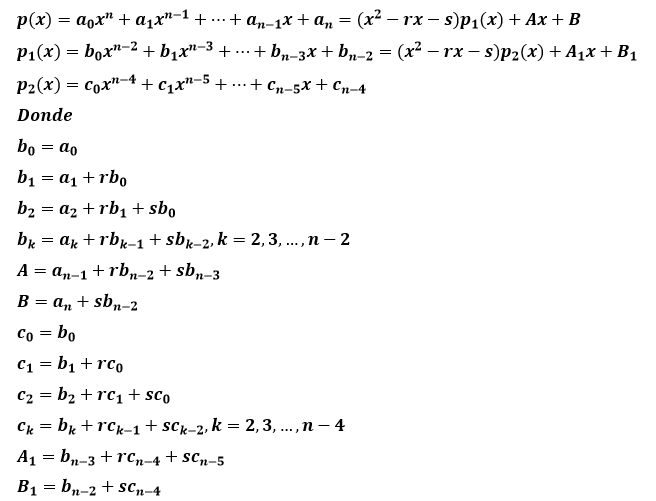
Resumiendo
Dado un polinomio de n potencia se encuentran dos factores, un polinomio cuadrático y un polinomio de grado n-2.
La principal diferencia de este método,
respecto a otros, es que permite calcular todas las raíces de un
polinomio (reales e imaginarias).
Recuerde la forma factorizada de un polinomio por ejemplo:
Si se divide entre un factor que no es
una raíz (por ejemplo, x+6), el cociente podría ser un polinomio de
cuarto orden. Sin embargo, en este caso, podría haber residuo. Con estas
bases se puede elaborar un algoritmo para determinar la raíz de un
polinomio:
- Suponiendo que el valor inicial de la raíz es x = t;
- Al dividir el polinomio entre el factor x – t,
- Determinando si existe un residuo, si no el valor es perfecto y la raíz es igual a t.
Si hay un residuo, el valor puede ser
ajustado sistemáticamente y el procedimiento repetirse hasta que el
residuo desaparezca y la raíz sea localizada.
El método de Bairstow se basa por lo general en esta aproximación. El proceso matemático depende de dividir el polinomio entre un factor.
El método de Bairstow se basa por lo general en esta aproximación. El proceso matemático depende de dividir el polinomio entre un factor.
Por ejemplo, Tomando el polinomio general con coeficientes iguales se tiene el polinomio general así:
Consecuentemente el proceso matemático
depende de dividir el polinomio fn(x) entre un factor, tomando en cuenta
la discusión del polinomio de deflación como sigue a continuación.
Supóngase que se tiene la raíz de orden n-esimo, y teniendo un adecuado procedimiento para eliminar la raíz encontrada, a este procedimiento de eliminar la raíz se le llama deflación polinomial.
Supóngase que se tiene la raíz de orden n-esimo, y teniendo un adecuado procedimiento para eliminar la raíz encontrada, a este procedimiento de eliminar la raíz se le llama deflación polinomial.
Tomando el polinomio y coeficientes en Orden Ascendente de la forma general de un polinomio de orden n:
Se tiene un polinomio:

Ahora suponga que se divide la función
polinomial de quinto orden por un factor de manera que se elimine una de
sus raíces por ejemplo el factor (x+3) y se tiene una función de cuarto
orden:
Con residuo cero para este caso.
Así se tiene que la forma general de un polinomio entre un factor x-t dará un segundo polinomio de un orden más bajo:
con residuo R=b0 en donde los coeficientes son obtenidos por la relación de recurrencia:
Para permitir la evaluación de raíces complejas este método divide la función entre el factor cuadrático:
Y aplicando la relación de recurrencia se obtiene los siguientes coeficientes para la ecuación anterior:
Se introduce el factor cuadrático para la
determinación de las raíces complejas, porque si los coeficientes del
polinomio original son reales, las raíces complejas se presentan en
pares conjugados.
Si 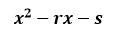 es
un divisor exacto del polinomio, las raíces complejas pueden ser
determinadas con la formula cuadrática, por lo que el método cuadrático
se reduce solo a determinar r y s que provocan que el factor cuadrático
sea un divisor exacto y por consiguiente se obtiene un residuo igual a
cero.
es
un divisor exacto del polinomio, las raíces complejas pueden ser
determinadas con la formula cuadrática, por lo que el método cuadrático
se reduce solo a determinar r y s que provocan que el factor cuadrático
sea un divisor exacto y por consiguiente se obtiene un residuo igual a
cero.
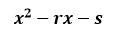 es
un divisor exacto del polinomio, las raíces complejas pueden ser
determinadas con la formula cuadrática, por lo que el método cuadrático
se reduce solo a determinar r y s que provocan que el factor cuadrático
sea un divisor exacto y por consiguiente se obtiene un residuo igual a
cero.
es
un divisor exacto del polinomio, las raíces complejas pueden ser
determinadas con la formula cuadrática, por lo que el método cuadrático
se reduce solo a determinar r y s que provocan que el factor cuadrático
sea un divisor exacto y por consiguiente se obtiene un residuo igual a
cero.
Entonces si 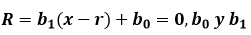 deben
ser cero. Esto para que los valores de inicio al evaluar r y s
conduzcan a este resultado, se debe de aplicar un camino para los
valores iniciales o de inicio de manera que b0 y b1 tiendan a cero para
ello se utiliza una técnica similar a la de Newton-Raphson.
deben
ser cero. Esto para que los valores de inicio al evaluar r y s
conduzcan a este resultado, se debe de aplicar un camino para los
valores iniciales o de inicio de manera que b0 y b1 tiendan a cero para
ello se utiliza una técnica similar a la de Newton-Raphson.
Pues b0 como b1 son funciones de r y s y se expanden utilizando la serie de Taylor:
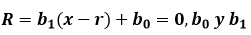 deben
ser cero. Esto para que los valores de inicio al evaluar r y s
conduzcan a este resultado, se debe de aplicar un camino para los
valores iniciales o de inicio de manera que b0 y b1 tiendan a cero para
ello se utiliza una técnica similar a la de Newton-Raphson.
deben
ser cero. Esto para que los valores de inicio al evaluar r y s
conduzcan a este resultado, se debe de aplicar un camino para los
valores iniciales o de inicio de manera que b0 y b1 tiendan a cero para
ello se utiliza una técnica similar a la de Newton-Raphson.Pues b0 como b1 son funciones de r y s y se expanden utilizando la serie de Taylor:
Los valores de la parte izquierda de la
igualdad son evaluados en r y s. Observe que el segundo término y el
término de orden superior se han despreciado. Ya que en forma implícita –
r y – s son muy pequeños y los términos de orden superior pueden ser
despreciados, pero otra consideraciones que los valores de inicio de son
tan cercanos a los valores de r y s de las raíces.
Para dar un valor inicial que se acerque a las raíces es el colocar las ecuaciones anteriores igual a cero y que resulte:
Si las variables ∆r y ∆s forman un
sistema de ecuaciones de dos incógnitas y el método de Bairstow muestra
que las derivadas parciales pueden resolverse por división sintética de
las b en forma similar al camino en que las b en sí mismas fueron
derivadas:
Entonces las derivadas parciales se
obtienen por división sintética de las b, y las b con las derivadas
parciales son sustituidas en las ecuaciones:
Y se obtiene:
Estas ecuaciones pueden ser resueltas
para mejorar los valores de r y s, se podría utilizar el error
aproximado para cada paso pero no es para nuestro caso realmente
utilizado pero quedaría de la siguiente forma:
Cuando los dos valores fallan bajo un criterio especificado las raíces pueden determinarse con la siguiente ecuación:
Aquí pueden caber tres posibilidades:
- El cociente es un polinomio de tercer orden o mayor. Para este caso, el método de Bairstow podría aplicarse al cociente para evaluar un nuevo valor de r y s. Los valores anteriores de r y s pueden servir como valores iniciales de para esta aplicación.
- El cociente es cuadrático. Para este caso, el residuo de las raíces puede evaluarse con la ecuación:

- El cociente es un polinomio de primer orden. Para este caso, el residuo es una sola raíz que puede evaluarse simplemente como: x=-s/r
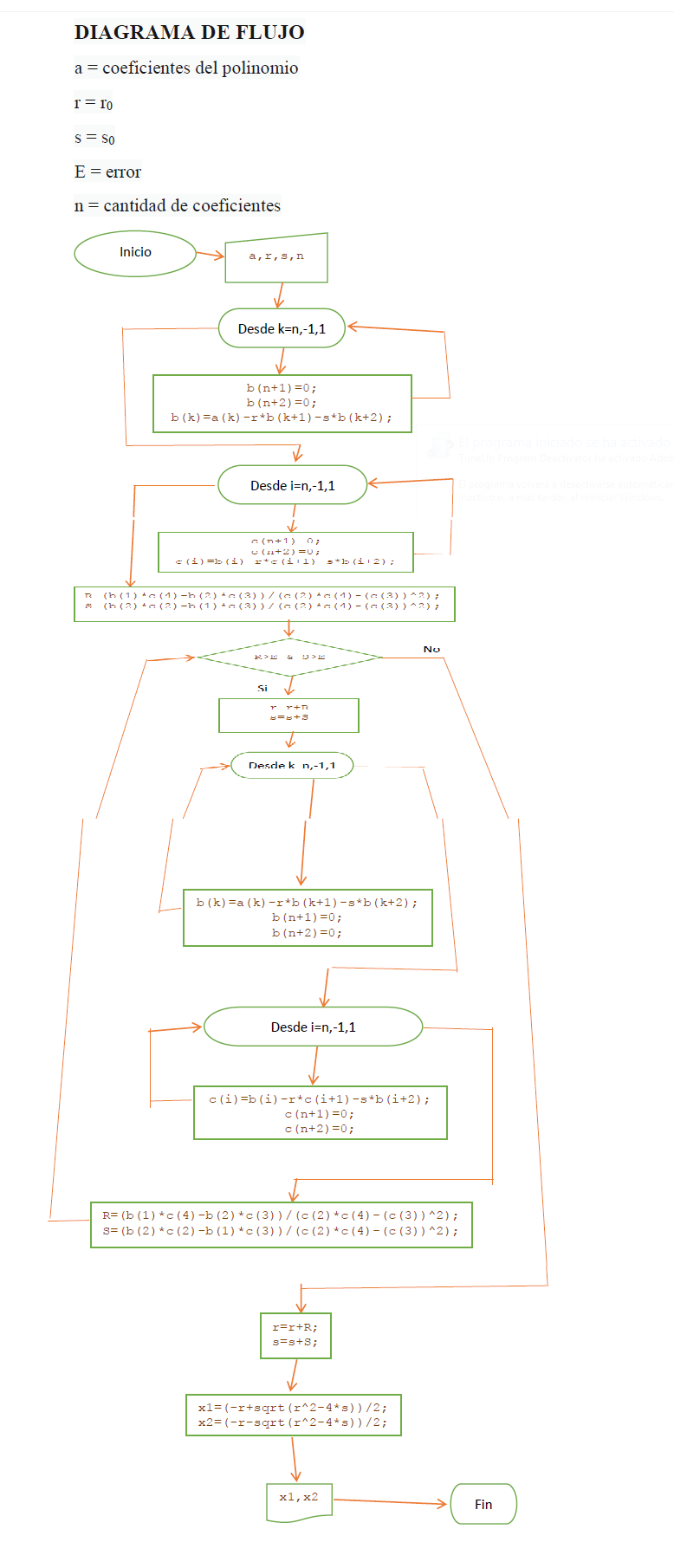
Algoritmo
Diagrama de Flujo
Resultados
- Comence ingresando los coeficientes de la funcion en orden decendente, esto quiere decir que primero se coloca el coeficiente que acompaña a la variable de mayor grado, y apartir de ahi desciende hasta llegar al termino que no acompaña variable.
- Se ingresan los valores iniciales de r0 y so, asi como el error bajo el cual se quiere trabajar.
- Damos aceptar
- Y a continuacion el programa arroja unos valores de x1=.05 y x2=-1
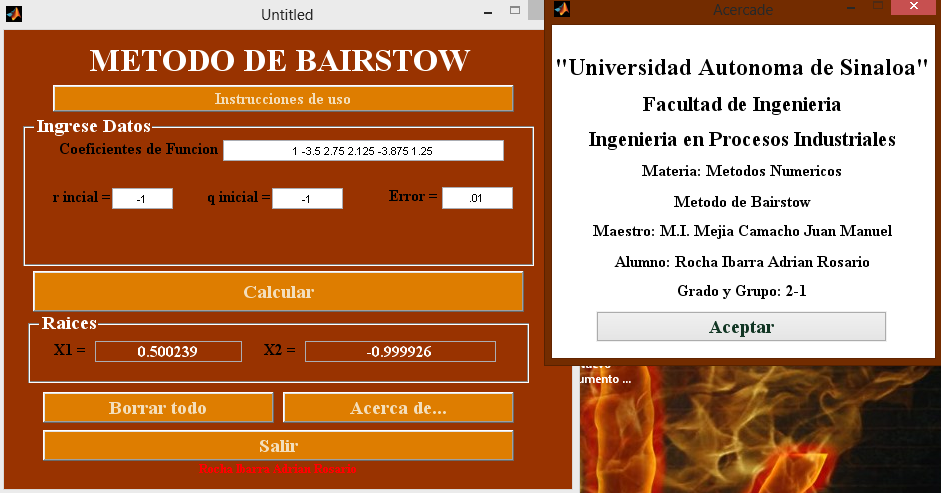
- x1=.05 y x2=-1 son dos raices reales del polinomio original de quinto grado f5(x)=x^5-3.5*x^4+2.75*x^3+2.125*x^2-3.875*x+1.25
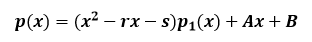












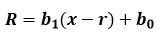


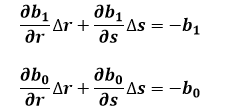






No hay comentarios:
Publicar un comentario