Interpolación polinómica
Contenidos
Polinomio interpolante
Problema Tenemos una serie de puntos  y0)
y0) (x1
(x1 y1)
y1)



 (xn
(xn yn)
yn)
Por ejemplo, si tenemos el conjunto de puntos:
 (2
(2 2)
2) (3
(3 6)
6) (4
(4 5)
5) (5
(5 5)
5) (6
(6 6)
6)
Dibujamos los puntos:
x=[2,3,4,5,6]; y=[2,6,5,5,6]; plot(x,y,'.','markersize',20)
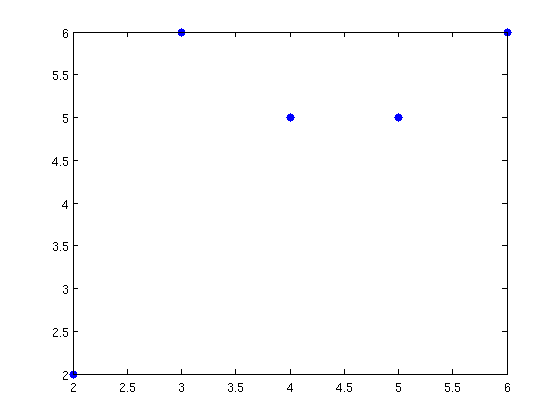
Solución con la matriz de Vandermonde
Como tenemos
es decir  a1
a1 a2
a2 a3
a3 a4
a4 y0)
y0) (x1
(x1 y1)
y1)



 (xn
(xn yn)
yn) n
n
Las ecuaciones serían:
Y el sistema a resolver es:
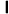
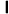
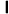
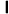
 1 1 1 1 1 x0 x1 x2 x3 x4 x20 x21 x22 x23 x24 x30 x31 x32 x33 x34 x40 x41 x42 x43 x44
1 1 1 1 1 x0 x1 x2 x3 x4 x20 x21 x22 x23 x24 x30 x31 x32 x33 x34 x40 x41 x42 x43 x44 
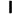
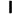
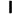
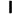
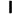
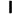
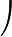
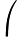
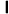
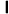
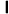
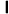
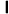
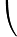 a0 a1 a2 a3 a4
a0 a1 a2 a3 a4 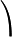
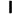
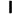
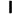
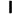
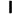
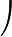 =
=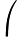
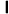
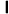
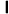
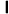
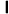
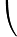 y0 y1 y2 y3 y4
y0 y1 y2 y3 y4 
La matriz de coeficientes del sistema se llama Matriz de Vandermonde.
Ejercicio 1
- Escribir una función V=Vandermonde(x) que tenga como argumentos de entrada el vector x y como argumento de salida la matriz de Vandermonde V.
- Calcular los coeficientes del polinomio resolviendo el sistema.
- Dibujar el polinomio
V=Vandermonde(x)
V =
1 2 4 8 16
1 3 9 27 81
1 4 16 64 256
1 5 25 125 625
1 6 36 216 1296
a=V\y' aa=a(end:-1:1)' % trasponemos a % y le damos la vuelta, % empezando por el coeficiente de mayor grado
a =
-75.0000
81.0000
-29.2500
4.5000
-0.2500
aa =
-0.2500 4.5000 -29.2500 81.0000 -75.0000
xx=linspace(min(x),max(x)); yy=polyval(aa,xx); % polyval % Entrada: % aa -> los coeficientes del polinomio % de mayor a menor % xx -> una serie de puntos % Salida: % yy -> valor del polinomio en esos puntos % plot(x,y,'.','markersize',20) % dibujamos los puntos hold on, plot(xx,yy) % dibujamos el polinomio
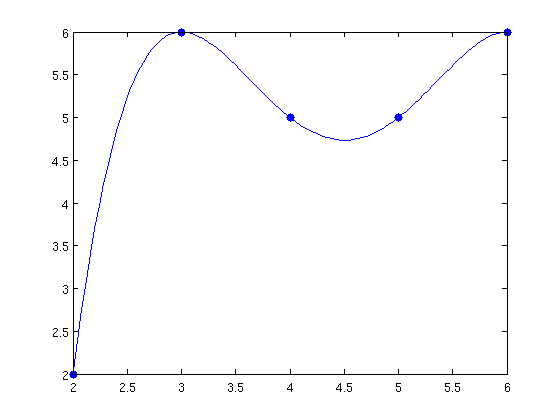
Existe una función Matlab que calcula la Matriz de Vandermonde. El orden de los elementos es distinto al que nosotros usamos:
vander(x)
ans =
16 8 4 2 1
81 27 9 3 1
256 64 16 4 1
625 125 25 5 1
1296 216 36 6 1
Pero este no es un método aconsejable porque la matriz de Vandermonde, en general, está mal condicionada y puede dar lugar a grandes errores en la solución del sistema.
Interpolación mediante los polinomios fundamentales de Lagrange
Para cada  1
1



 n
n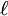 k
k n
n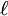 k
k xj
xj =
= kj
kj
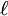 k
k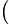 z
z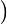 =(z−x0)
=(z−x0)

 (z−xk−1)(z−xk+1)
(z−xk−1)(z−xk+1)

 (z−xn)(xk−x0)
(z−xn)(xk−x0)

 (xk−xk−1)(xk−xk+1)
(xk−xk−1)(xk−xk+1)

 (xk−xn)
(xk−xn) 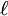 0
0
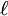 1
1




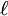 n
n
polinomios_fundamentales_de_Lagrange
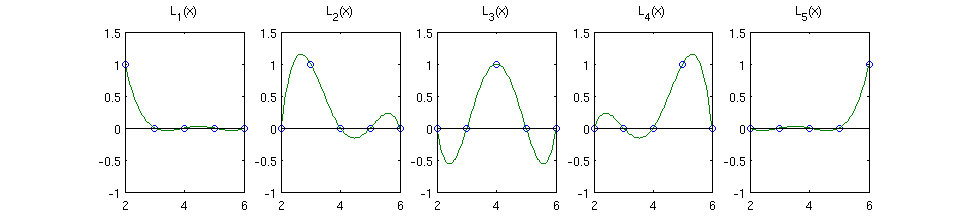
Vemos que valen
Si multiplicamos cada uno de los polinomios fundamentales de Lagrange por su correspondiente 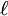 0
0 y1
y1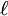 1
1



 yn
yn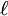 n
n
polinomios_fundamentales_de_Lagrange_por_y
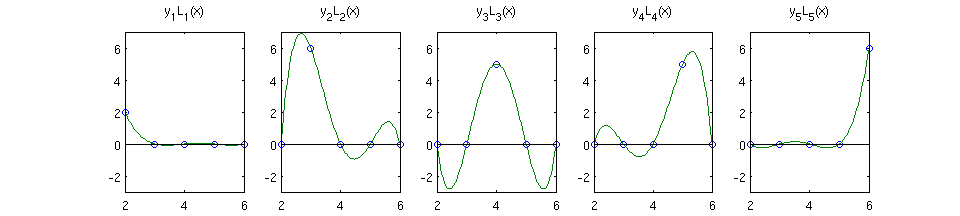
Vemos que valen
El polinomio de interpolación de Lagrange en los puntos  x1
x1



 xn
xn y1
y1



 yn
yn
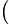 x
x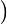 =y0
=y0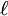 0
0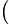 x
x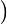 +y1
+y1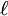 1
1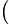 x
x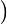 +
+

 +yn
+yn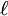 n
n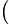 x
x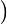
Y si sumamos estos cinco polinomios
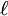 0(x)+
0(x)+

 +y4
+y4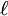 4(x)
4(x)obtenemos el polinomio interpolante de Lagrange
polinomio_interpolante_Lagrange

El inconveniente de este método es que si queremos incorporar un nodo nuevo tenemos que rehacer todos los cálculos.
Interpolación mediante diferencias divididas
Fórmula de Newton
El polinomio de interpolación de Lagrange en los puntos  x1
x1



 xn
xn y1
y1



 yn
yn
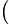 x
x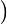 =
=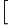 y0
y0 +
+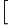 y0
y0 y1
y1
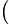 x−x0
x−x0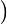 +
+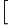 y0
y0 y1
y1 y2
y2
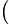 x−x0
x−x0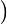
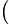 x−x1
x−x1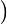 +
+

 +
+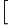 y0
y0 y1
y1



 yn
yn
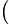 x−x0
x−x0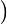
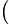 x−x1
x−x1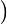



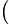 x−xn−1
x−xn−1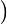
Tabla de diferencias divididas
Los coeficientes del polinomio anterior son la primera fila de la tabla:


 xn−1 xn y0 y1 y2
xn−1 xn y0 y1 y2 

 yn−1 yn
yn−1 yn 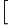 y0
y0 y1
y1 =x0−x1y0−y1
=x0−x1y0−y1 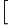 y1
y1 y2
y2 =x1−x2y1−y2
=x1−x2y1−y2 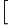 y2
y2 y3
y3 =x2−x3y2−y3
=x2−x3y2−y3 


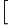 yn−1
yn−1 yn
yn =xn−1−xnyn−1−yn
=xn−1−xnyn−1−yn 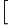 y0
y0 y1
y1 y2
y2 =x0−x2
=x0−x2 y0
y0 y1
y1 −
− y1
y1 y2
y2
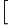 y1
y1 y2
y2 y3
y3 =x1−x3
=x1−x3 y1
y1 y2
y2 −
− y2
y2 y3
y3
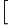 y2
y2 y3
y3 y4
y4 =x2−x4
=x2−x4 y2
y2 y3
y3 −
− y3
y3 y4
y4















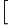 y0
y0 y1
y1



 yn
yn =x0−xn
=x0−xn y0
y0



 yn−1
yn−1 −
− y1
y1



 yn
yn
Con este método, si añadimos un nodo, no hay que rehacer todos los cálculos, sino que se añade una línea más a la tabla anterior en su parte inferior.
Ejercicio 2 Escribir una función a=difdiv(x,y) que calcule la matriz a que contiene la tabla de diferencias divididas de Newton para los puntos contenidos en x, y. No almacenar x en a. Utilizar la matriz a para calcular el polinomio interpolante en la forma de Newton. Dibujar el polinomio interpolante y los puntos.
x=[2,3,4,5,6]; y=[2,6,5,5,6]; a=difdiv(x,y)
a =
2.0000 4.0000 -2.5000 1.0000 -0.2500
6.0000 -1.0000 0.5000 0 0
5.0000 0 0.5000 0 0
5.0000 1.0000 0 0 0
6.0000 0 0 0 0
xx=linspace(min(x),max(x)); yy=pol_newton(x,a,xx); plot(x,y,'.','markersize',10) hold on,plot(xx,yy)
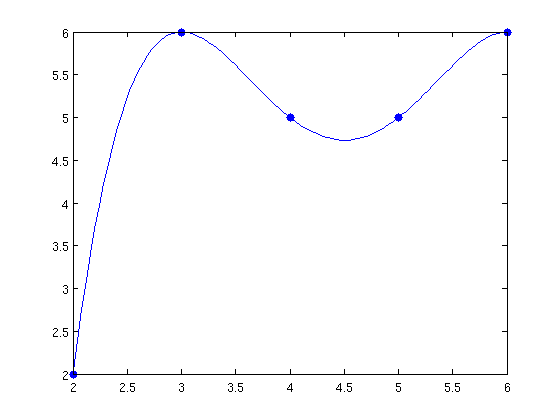
Interpolación con órdenes Matlab
El polinomio de interpolación se puede obtener con el comando de Matlab polyfit escogiendo como grado del polinomio el número de puntos menos uno. Nos da los coeficientes del polinomio interpolante en un vector, empezando por el de mayor grado:
x=[2,3,4,5,6];
y=[2,6,5,5,6];
pol=polyfit(x,y,length(x)-1); % coeficientes del polinomio
Representamos el polinomio:
xx=linspace(min(x),max(x)); yy=polyval(pol,xx); plot(x,y,'.','markersize',20) hold on,plot(xx,yy)

Ejercicio 3 Escribir una función cheby(f,a,b,n) que interpole la función f en el intervalo [a,b] utilizando n nodos:
- Utilizando nodos equiespaciados incluyendo los extremos del intervalo.
- Utilizando nodos de Chebyshev:
xi(n)=cos2n 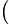 2i−1
2i−1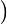
 i=1
i=1 2
2



 n
n
En el intervalo 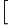 −1
−1 1
1
En ambos casos dibujar los nodos, la función y el polinomio interpolador.
f=@(x) (1)./(1+25*x.^2); cheby(f,-1,1,11)

Podemos obtener la interpolación lineal a trozos con polinomios de grado cero con la orden interp1 y la opción nearest
x=[2,3,4,5,6]; y=[2,6,5,5,6]; xx=linspace(min(x),max(x),1000); yy=interp1(x,y,xx,'nearest'); plot(x,y,'.','markersize',20) axis([2 6 1 7]) hold on, plot(xx,yy),hold off

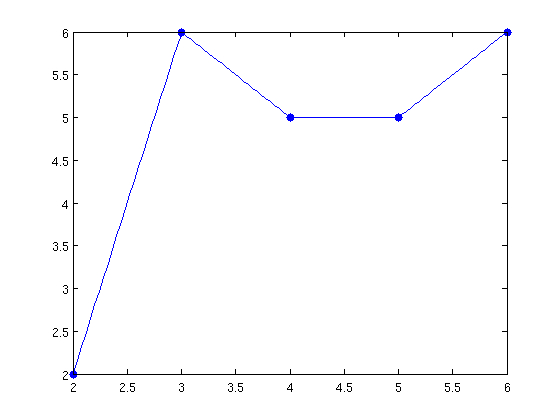
Y con polinomios de grado uno (o lo que es lo mismo, interpolación lineal a trozos) con la orden interp1 y la opción linear
x=[2,3,4,5,6]; y=[2,6,5,5,6]; xx=linspace(min(x),max(x)); yy=interp1(x,y,xx,'linear'); plot(x,y,'.','markersize',20) hold on, plot(xx,yy), hold off
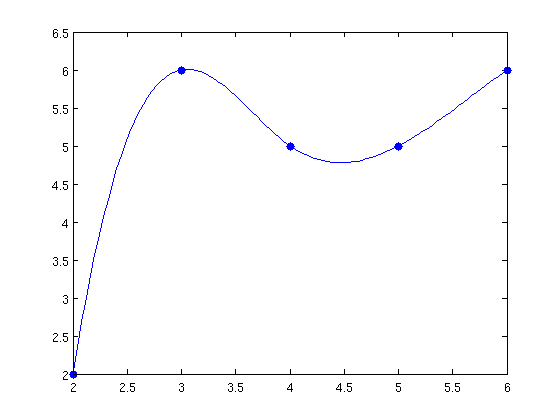
Y la interpolación con splines (con la opción not-a-knot) con la orden
yy = spline(x,y,xx); plot(x,y,'.','markersize',20) hold on, plot(xx,yy), hold off
Ejercicio 4 Realizar una programa error_max que, para la función  10]
10] 1
1



 10
10
- Lineal a trozos.
- Con splines.
y calcule, para los puntos puntos=0:0.01:10 el error máximo en cada caso. ¿Qué interpolación da mayor error máximo?
error_max
Error interpolación lineal a trozos = 0.12207 Error interpolación con splines = 0.024833

No hay comentarios:
Publicar un comentario