https://www.lifeder.com/regla-sturges/
Regla de Sturges: Explicación, Aplicaciones y Ejemplos
La regla de Sturges es un criterio utilizado para determinar el número de clases o intervalos que son necesarios para representar gráficamente un conjunto de datos estadísticos. Esta regla fue enunciada en 1926 por el matemático alemán Herbert Sturges.
Sturges propuso un método sencillo, basado en el número de muestras x que permitiesen encontrar el número de clases y su amplitud de rango. La regla de Sturges es muy utilizada sobre todo en el área de la estadística, específicamente para construir histogramas de frecuencia.
Explicación
La regla de Sturges es un método empírico muy utilizado en la estadística descriptiva para determinar el número de clases que deben existir en un histograma de frecuencias, para así poder clasificar un conjunto de datos que representan una muestra o población.
Básicamente, con esta regla se determina el ancho de los contenedores gráficos, de los histogramas de frecuencia.
Para establecer su regla Herbert Sturges consideró un diagrama de frecuencias ideal, que consta de K intervalos, donde el i-ésimo intervalo contiene un determinado número de muestras (i = 0,… k – 1), representado como:
Ese número de muestras es dado por el número de formas en que puede extraerse un subconjunto de un conjunto; es decir, por el coeficiente binomial, expresado de la siguiente manera:
Para simplificar la expresión, aplicó las propiedades de los logaritmos en ambas partes de la ecuación:
Así, Sturges estableció que el número óptimo de intervalos k es dado por la expresión:
También puede ser expresada como:
En esta expresión:
– k es el número de clases.
– N es el número total de observaciones de la muestra.
– Log es el logaritmo común de base 10.
Por ejemplo, para elaborar un histograma de frecuencia que exprese una muestra aleatoria de la estatura de 142 niños, el número de intervalos o clases que tendrá la distribución es:
k=1 + 3,322 * log10 (N)
k=1+3,322* log (142)
k=1+3,322* 2,1523
k=8,14 ≈ 8
Así, la distribución será en 8 intervalos.
El número de intervalos siempre debe estar representado por números enteros. En los casos en los que el valor sea decimal, se debe hacer una aproximación al número entero más próximo.
Aplicaciones
La regla de Sturges es aplicada principalmente en estadística, ya que esta permite realizar una distribución de frecuencias a través del cálculo del número de clases (k), así como la longitud de cada una de estas, conocida también como amplitud.
La amplitud es la diferencia del límite superior e inferior de la clase, dividido entre el número de clases, y se expresa:
Existen muchas reglas empíricas que permiten hacer una distribución de frecuencias. Sin embargo, la regla de Sturges es comúnmente usada porque hace una aproximación del número de clases, que generalmente va de 5 a 15.
De esa forma, considera un valor que representa adecuadamente una muestra o población; es decir, la aproximación no representa agrupaciones extremadas, así como tampoco trabaja con un número excesivo de clases que no permitan resumir la muestra.
Ejemplo
Se necesita realizar un histograma de frecuencia de acuerdo a los datos dados, que corresponden a edades obtenidas en una encuesta realizada a hombres que hacen ejercicios en un gimnasio de la localidad.
Para determinar los intervalos se debe saber cuál es el tamaño de la muestra o el número de observaciones; en este caso, se tienen 30.
Luego se aplica la regla de Sturges:
k=1 + 3,322 * log10 (N)
k=1+3,322* log (30)
k=1+3,322* 1,4771
k = 5,90 ≈ 6 intervalos.
A partir del número de intervalos, se puede calcular la amplitud que estos van a tener; es decir, la anchura de cada barra representada en el histograma de frecuencias:
El límite inferior es considerado como el valor menor de los datos, y el superior es el valor mayor. La diferencia entre el límite superior e inferior es denominada rango o recorrido de la variable (R).
De la tabla se tiene que el límite superior es 46 y el inferior 13; de esa manera, la amplitud de cada clase será:
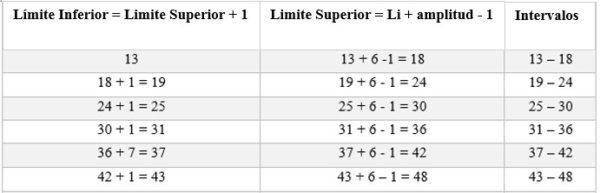
Los intervalos estarán compuestos por un límite superior e inferior. Para determinar esos intervalos se comienza contando desde el límite inferior, sumándole a este la amplitud determinada por la regla (6), de la siguiente manera:
Luego se calcula la frecuencia absoluta para determinar el número de hombres que corresponden a cada intervalo; en este caso es:
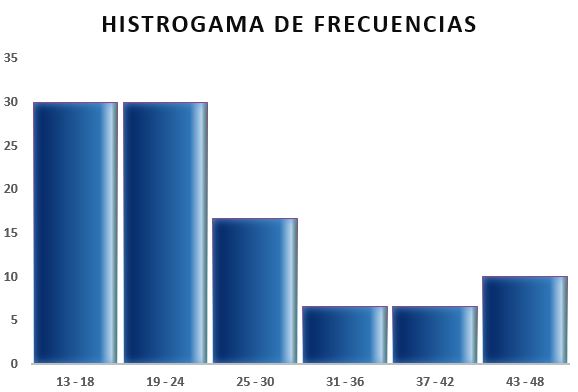
– Intervalo 1: 13 – 18 = 9
– Intervalo 2: 19 – 24 = 9
– Intervalo 3: 25 – 30 = 5
– Intervalo 4: 31 – 36 = 2
– Intervalo 5: 37 – 42 = 2
– Intervalo 6: 43 – 48 = 3
Al sumar la frecuencia absoluta de cada clase, esta debe ser igual al número total de la muestra; en este caso, 30.
Posteriormente se calcula la frecuencia relativa de cada intervalo, dividiendo la frecuencia absoluta de esta entre el número total de observaciones:
– Intervalo 1: fi = 9 ÷ 30 = 0,30
– Intervalo 2: fi = 9 ÷ 30 = 0,30
– Intervalo 3: fi = 5 ÷ 30 = 0,1666
– Intervalo 4: fi = 2 ÷ 30 = 0,0666
– Intervalo 5: fi = 2 ÷ 30 = 0,0666
– Intervalo 4: fi = 3 ÷ 30 = 0,10
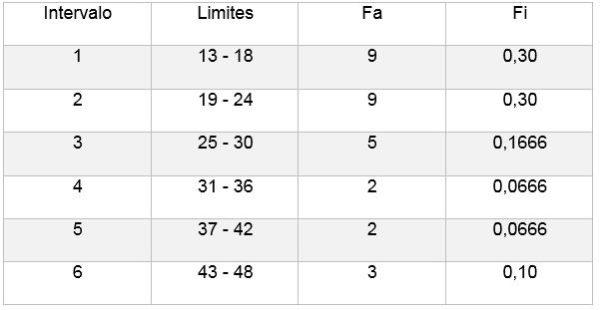
Luego se puede realizar una tabla que refleje los datos, y también el diagrama a partir de la frecuencia relativa con relación a los intervalos obtenidos, como se puede observar en las siguientes imágenes:
De esa manera, la regla de Sturges permite determinar la cantidad de clases o intervalos en los que puede ser dividida una muestra, con la finalidad de resumir una muestra de datos a través de la elaboración de tablas y gráficas.
Referencias
- Alfonso Urquía, M. V. (2013). Modelado Y Simulación De Eventos Discretos. UNED,.
- Altman Naomi, M. K. (2015). “Simple Linear Regression.” Nature Methods .
- Antúnez, R. J. (2014). Estadística en la educación. Digital UNID.
- Fox, J. ( 1997.). Applied Regression Analysis, Linear Models, and Related Methods. SAGE Publications.
- Humberto Llinás Solano, C. R. (2005). Estadística descriptiva y distribuciones de probabilidad. Universidad del Norte.
- Panteleeva, O. V. (2005). Fundamentos de Probabilidad y Estadística.
- O. Kuehl, M. O. (2001). Diseño de Experimentos: Principios Estadísticos de Diseño Y análisis de Investigación. Thomson Editores.
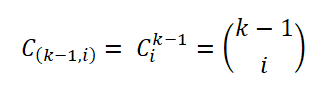
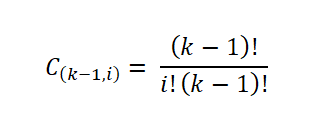
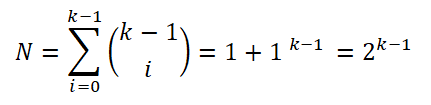
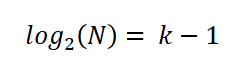
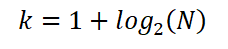
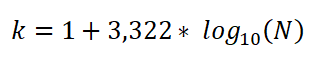
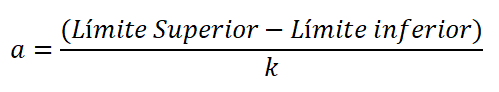

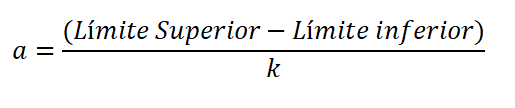
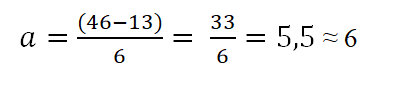
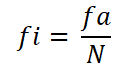
No hay comentarios:
Publicar un comentario