Demostración del seno de una suma de ángulos

Demostración del seno de una suma de ángulos

https://www.matesfacil.com/ESO/trigonometria/suma/demostraciones-seno-coseno-tangente-suma.html

https://www.geogebra.org/m/k8uszyzh#:~:text=Esto%20se%20debe%20a%20que,es%20la%20hipotenusa%20del%20tri%C3%A1ngulo.

1. Seno de la suma de ángulos

Ver demostración

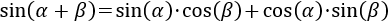
Nos apoyaremos en la siguiente representación:

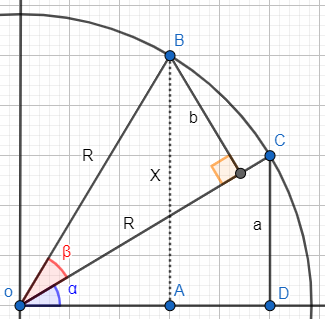
Como el radio de la circunferencia es $R=1$, entonces

• El segmento $a$ es el seno ángulo $\alpha$.

• El segmento $b$ es el seno del ángulo $\beta$.

• El segmento $X$ (segmento discontinuo) es el seno del ángulo $\alpha +\beta$.

Ahora vamos a calcular el segmento $X$, es decir, el seno de la suma de los ángulos: $sin(\alpha +\beta )$.

Trazamos el segmento $m$ paralelo al segmento $a$:

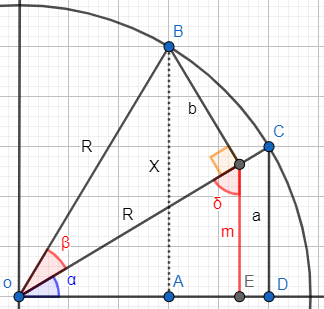
El ángulo $\delta$ que aparece mide $\delta ={90}^{\circ }-\alpha$. Esto se debe a que los dos otros ángulos del triángulo miden $\alpha$ y ${90}^{\circ }$ y la suma de los tres ángulos debe ser ${180}^{\circ }$:

$$\delta ={180}^{\circ }-\alpha -{90}^{\circ }$$

$$\delta ={90}^{\circ }-\alpha$$

Teniendo en cuenta la introducción, el lado $m$ del triángulo es

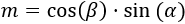
Nota: $cos\left(\beta \right)$ multiplica al seno porque es la hipotenusa del triángulo.

Prolongamos el segmento $m$ obteniendo el segmento $p$ (el segmento $m$ no cambia):

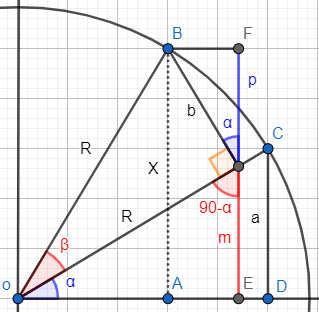
Observando la figura,

• El segmento $X$ mide lo mismo que la suma de los lados $m$ y $p$.

• El nuevo ángulo representado mide $\alpha$ porque junto con los ángulos ${90}^{\circ }$ y ${90}^{\circ }-\alpha$ debe sumar ${180}^{\circ }$.

• Teniendo en cuenta la introducción, el lado $p$ del triangulo superior es

  

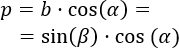
Por tanto, el segmento $X$ es

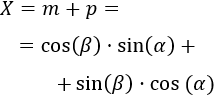
Como queríamos demostrar.