Ecuaciones del plano

Deducción de la ecuación general del plano

https://aga.frba.utn.edu.ar/ecuaciones-del-plano/

Dada una dirección en $R^{3}$ , existen infinitos planos perpendiculares a la misma. Si conocemos además un punto del plano, éste queda determinado de forma única.

Nos proponemos hallar la ecuación del plano $π$ que pasa por $P_{0} (x_{0}, y_{0}, z_{0})$ y es perpendicular al vector $\vec{n} = (a, b, c) .$ El vector $\vec{n}$ se denomina vector normal del plano.

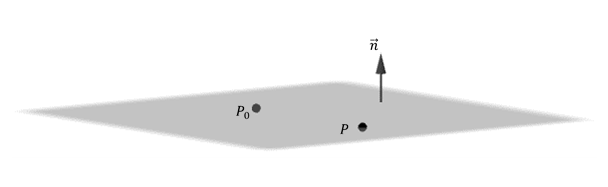
¿Qué condición debe cumplir un punto $P (x, y, z)$ para estar en el plano $π$ ? Si armamos el vector $\vec{P_{0} P}$ , éste debe ser paralelo al plano, o sea perpendicular al vector normal del plano:

$P (x, y, z) \in π \Leftrightarrow \vec{P_{0} P} ⊥ \vec{n} \Leftrightarrow \vec{P_{0} P} . \vec{n} = 0$

$(x - x_{0}, y - y_{0}, z - z_{0}) . (a, b, c) = 0$

$a (x - x_{0}) + b (y - y_{0}) + c (z - z_{0}) = 0$

a x + b y + c z + d = 0 E c u a c i ó n g e n e r a l o i m p l í c i t a d e l p l a n o

Ejemplo

Hallar la ecuación del plano perpendicular al vector $\vec{n} = (3, 2, 1)$ que pasa por el punto $P_{0} (1, 1, - 1)$ .

Las componentes de $\vec{n}$ nos indican los coeficientes $a$ , $b$ y $c$ de la ecuación del plano:

$π : 3 x + 2 y + z + d = 0$

¿Cómo hallamos $d$ ?

El punto debe verificar la ecuación, entonces reemplazamos $P_{0}$ y obtenemos el coeficiente que faltaba:

$3.1 + 2.1 - 1 + d = 0 \Rightarrow d = - 4$

Así obtenemos la ecuación del plano:

$π : 3 x + 2 y + z - 4 = 0$

Éste es el único plano que pasa por el punto $P_{0}$ y es perpendicular al vector $\vec{n}$ .

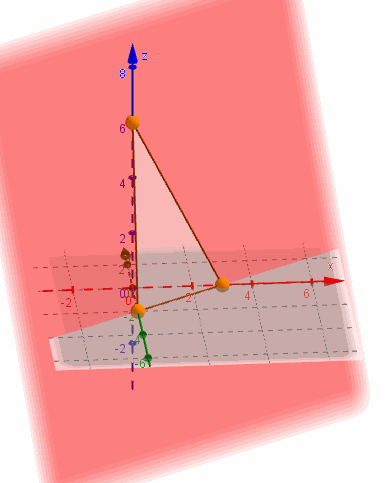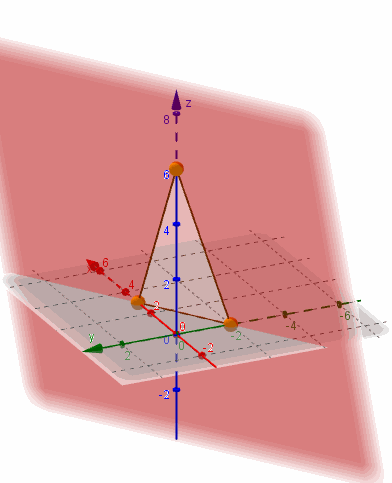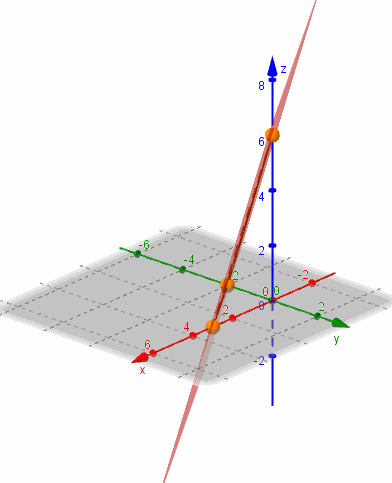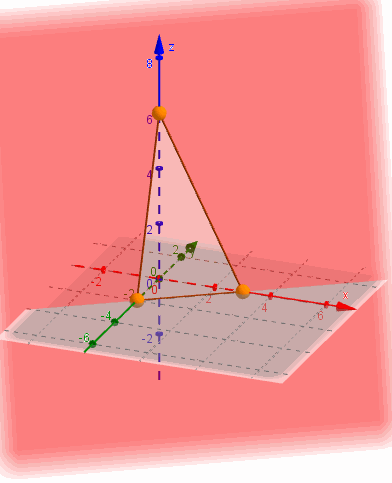
Para efectuar un gráfico aproximado del plano que obtuvimos, podemos buscar sus intersecciones con los ejes coordenados:

Para hallar la intersección con el eje $x$ , debemos plantear $y = z = 0$ y despejar el valor de $x$ . Análogamente para las otras intersecciones, tal como se muestra en el siguiente cuadro:

como graficar un plano

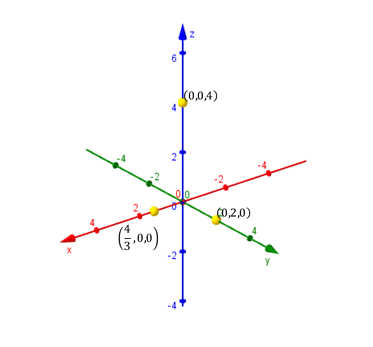
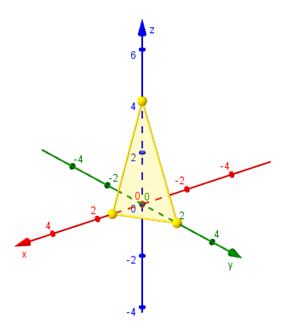
Tres puntos no alineados determinan un único plano que los contiene. Trazamos los segmentos que unen los puntos hallados y obtenemos la representación gráfica de una porción del plano:

Mostramos una gráfica del plano realizada con GeoGebra:

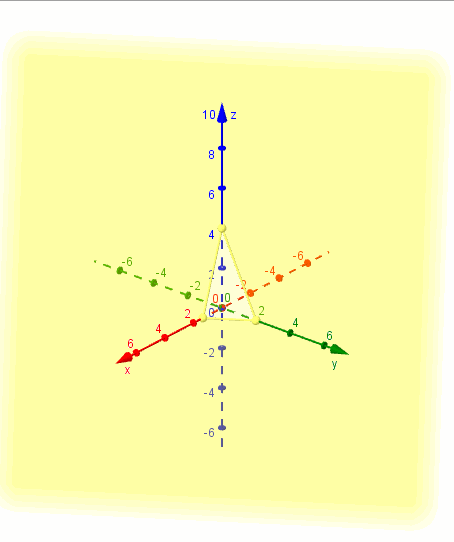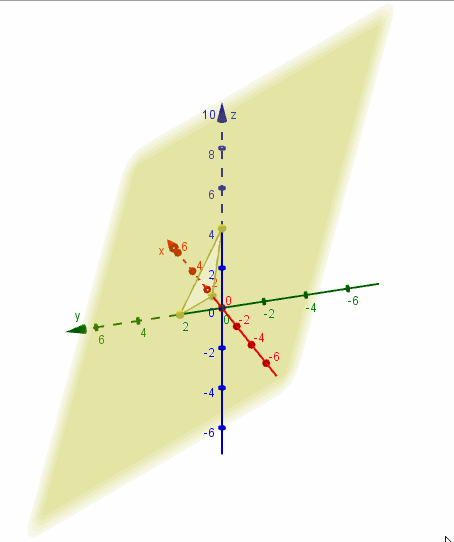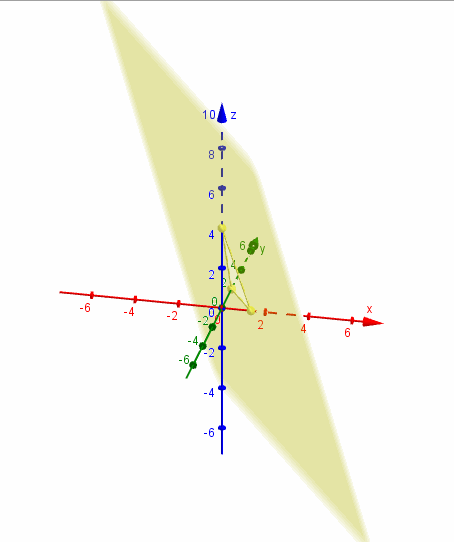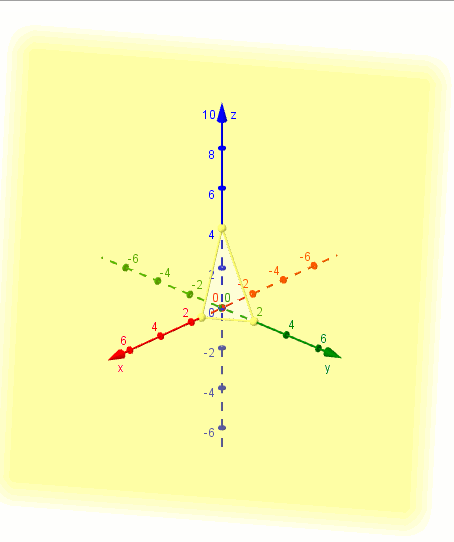
gif020-plano

Ejemplo

Dados los puntos $R (1, 2, 3)$ y $S (3, - 1, 2)$ , encontrar la ecuación del plano que corta perpendicularmente al segmento $R S$ en su punto medio.

Resolución

Busquemos las coordenadas del punto medio:

$M = (\frac{1 + 3}{2}, \frac{2 + (- 1)}{2}, \frac{3 + 2}{2}) = (2, \frac{1}{2}, \frac{5}{2})$

Como el plano corta perpendicularmente al segmento $R S$ , podemos tomar $\vec{R S}$ como vector normal del plano:

$\vec{R S} = (2, - 3, - 1)$

Escribimos la ecuación del plano al que llamaremos $β$ :

$β : 2 x - 3 y - 1 z + d = 0$

Para hallar $d$ reemplazamos el punto $M$ :

$2.2 - 3. \frac{1}{2} - \frac{5}{2} + d = 0 \Rightarrow d = 0$

Y así obtenemos la ecuación buscada:

$β : 2 x - 3 y - z = 0$

Este plano pasa por el origen, o sea que interseca a los tres ejes en $(0, 0, 0)$ . Necesitamos al menos dos puntos más para graficarlo.

Para facilitar el gráfico podemos elegir puntos que estén sobre los planos coordenados. Por ejemplo $y = 0$ :

$\Rightarrow 2 x - z = 0 \Rightarrow z = 2 x$

Entonces haciendo que $x = 1$ debe ser $z = 2$ , y obtenemos el punto $P_{1} (1, 0, 2)$

Para tomar otro punto del plano podemos hacer que $z = 0$

$\Rightarrow 2 x - 3 y = 0 \Rightarrow y = \frac{2}{3} x$

Y si $x = 3$ entonces $y = 2$ . Obtenemos el punto $P_{2} (3, 2, 0)$

Entonces $β$ contiene a los puntos $(0, 0, 0), (1, 0, 2)$ y $(3, 2, 0)$ :

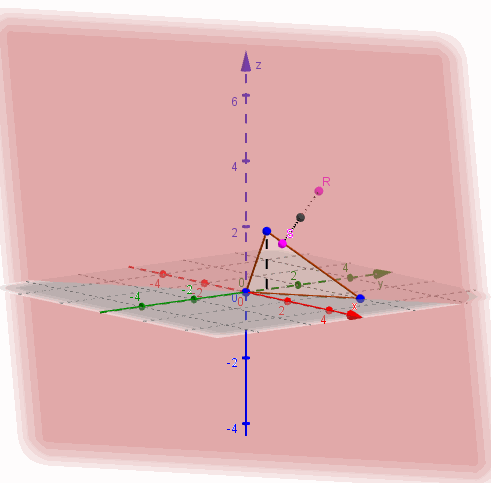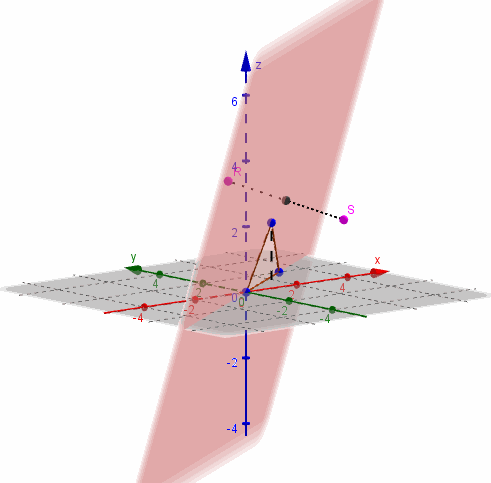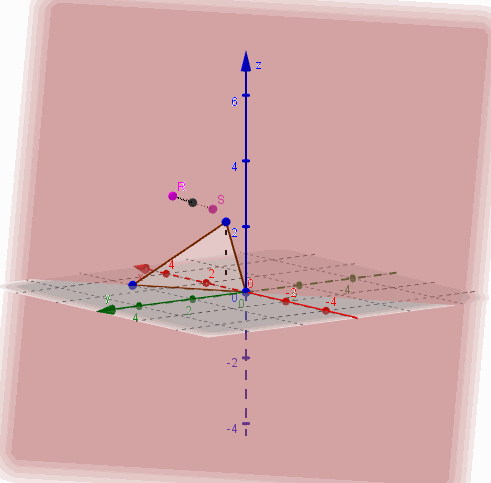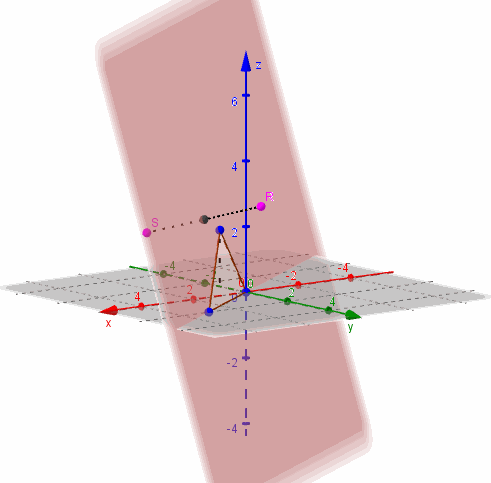
gif006-plano-que-pasa-por-el-origen-1

Ejemplo

Dados $A (4, 5, 2), B (1, 3, 4)$ , $C (2, 2, 5)$ hallar, si es posible, el plano que contiene a los tres puntos.

Habíamos dicho que tres puntos no alineados determinan un único plano que los contiene.

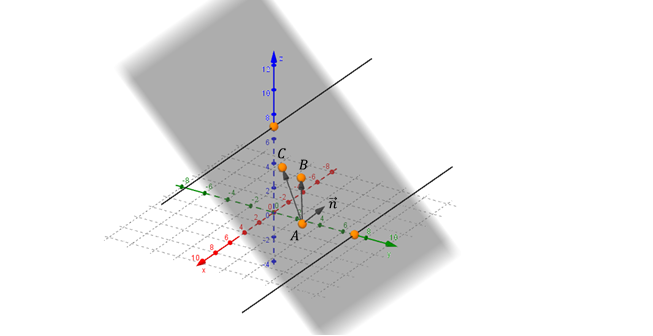
Hagamos una figura de análisis:

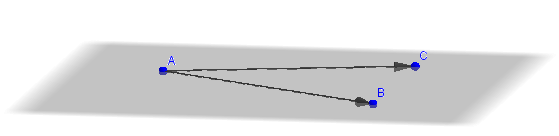
Con los tres puntos, podemos armar dos vectores, por ejemplo:

$\vec{A B} = (- 3, - 2, 2)$

$\vec{A C} = (- 2, - 3, 3)$

El vector normal debe ser perpendicular a ambos vectores cómo muestra la siguiente figura:

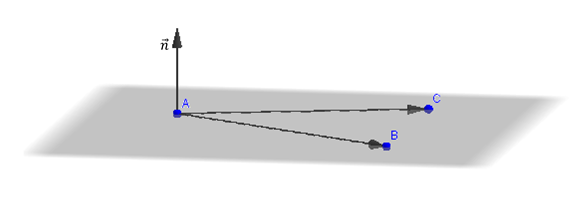
¿Qué operación nos permite hallar un vector perpendicular a otros dos?

$(\vec{A B} \times \vec{A C} = (0, 5, 5)$

¿Qué resultado habríamos obtenido si $A$ , $B$ y $C$ estuvieran alineados?

El vector $(0, 5, 5)$ es perpendicular al plano que buscamos, entonces podemos tomar $\vec{n} = (0, 5, 5)$ y escribir la ecuación del plano:

$α : 5 y + 5 z + d = 0$

Para hallar $d$ podemos reemplazar cualquiera de los tres puntos. Reemplacemos $A$ :

$5.5 + 5.2 + d = 0 \Rightarrow d = - 35$

Luego:

$5 y + 5 z - 35 = 0$

Podemos dividir por 5 ambos miembros:

$α : y + z - 7 = 0$

El lector puede comprobar que los puntos $B$ y $C$ verifican esta ecuación.

Busquemos las intersecciones con los ejes para graficar el plano:

$y = z = 0 \Rightarrow - 7 = 0 A b s u r d o$

Entonces $α$ no corta al eje $x$ .

¿En qué punto corta al eje $y$ ? $(0, 7, 0)$

¿Y al eje $z$ ? $(0, 0, 7)$

Observemos que el plano contiene a todos los puntos de la forma $(x, 7, 0)$ con $x \in R .$

Lo mismo ocurre con los puntos del tipo $(x, 0, 7)$ con $x \in R .$

Podemos observar entonces que:

$a = 0 \Rightarrow e l p l a n o e s ∥ a l e j e x$

Ecuación segmentaria del plano

Dada la ecuación general de un plano:

$π : a x + b y + c z + d = 0$

Si $a, b, c, d$ son distintos de cero, es posible obtener otra ecuación del plano como sigue:

$a x + b y + c z = - d$

$\frac{a}{- d} x + \frac{b}{- d} y + \frac{c}{- d} z = 1$

$\frac{x}{(- \frac{d}{a})} + \frac{y}{(- \frac{d}{b})} + \frac{z}{(- \frac{d}{c})} = 1$

Si llamamos $p = - \frac{d}{a}$ , $q = - \frac{d}{b}$ , $r = - \frac{d}{c}$

Resulta:

\frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 E c u a c i ó n s e g m e n t a r i a d e l p l a n o

Veamos qué indican $p$ , $q$ y $r$ :

¿Cuál es la intersección del plano con el eje x?

¿Cuál es la intersección con el eje y?

$(0, q, 0)$

¿Y con el eje z?

$(0, 0, r)$

Podemos observar que p, q y r indican las intersecciones con los ejes.

Ejemplo

$2 x - 3 y + z - 6 = 0$

$2 x - 3 y + z = 6$

$\frac{2 x}{6} - \frac{3 y}{6} + \frac{z}{6} = 1$

$\frac{x}{3} - \frac{y}{2} + \frac{z}{6} = 1$

Esta ecuación parece segmentaria pero no lo es por el signo negativo. La reescribimos así:

$\frac{x}{3} + \frac{y}{- 2} + \frac{z}{6} = 1 E c u a c i ó n s e g m e n t a r i a$

La ecuación segmentaria es práctica para graficar un plano porque muestra los tres puntos de corte con los ejes:

gif010

Ecuación vectorial paramétrica del plano

Dados dos vectores $\vec{u} = (u_{1}, u_{2}, u_{3})$ y $\vec{v} = (v_{1}, v_{2}, v_{3})$ no paralelos y un punto $P_{0} (x_{0}, y_{0}, z_{0})$ , nos proponemos hallar la ecuación del plano $π$ que pasa por $P_{0}$
y es paralelo a $\vec{u}$ y $\vec{v}$ .

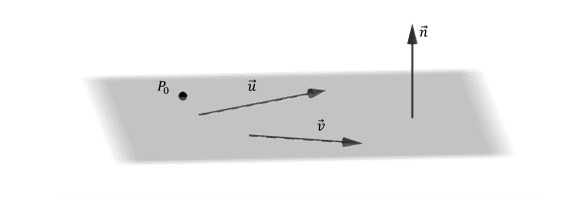
¿Cómo podemos obtener un vector perpendicular al plano conociendo dos vectores paralelos a dicho plano?

$\vec{n} = \vec{u} \times \vec{v}$

Teniendo $\vec{n}$ y el punto $P_{0}$ , podemos hallar la ecuación implícita o general del plano $π$ como habíamos visto previamente.

Obtendremos a continuación otro tipo de ecuación del plano, cuya deducción se basa en el concepto de combinación lineal de vectores, tal cómo vimos en el ejemplo.

Si $P (x, y, z)$ es un punto cualquiera del plano $π$ , los vectores $\vec{P_{0} P}, \vec{u} y \vec{v}$ son coplanares

Entonces

$\exists α, β \in R | \vec{P_{0} P} = α \vec{u} + β \vec{v}$

Esto significa que el vector $\vec{P_{0} P}$ puede expresarse como combinación lineal de $\vec{u}$ y $\vec{v}$ , como se muestra en la figura:

$(x - x_{0}, y - y_{0}, z - z_{0}) = α . (u_{1}, u_{2}, u_{3}) + β (v_{1}, v_{2}, v_{3})$

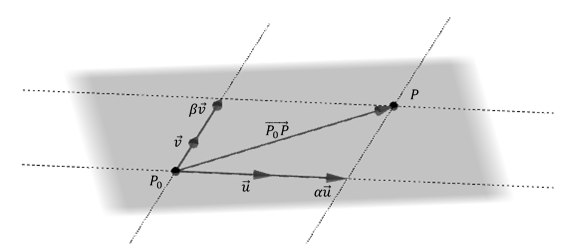
Por lo tanto:

$(x, y, z) = (x_{0}, y_{0}, z_{0}) + α (u_{1}, u_{2}, u_{3}) + β (v_{1}, v_{2}, v_{3})$ , $c o n α, β \in R$

O en notación vectorial:

(x, y, z) = \vec{O P_{0}} + α . \vec{u} + β . \vec{v} E c u a c i ó n v e c t o r i a l p a r a m é t r i c a d e l p l a n o

Ejemplo

Armar la ecuación vectorial paramétrica del plano paralelo a $\vec{u} = (3, - 1, 5)$ y $\vec{v} = (7, 3, 2)$ que pasa por el punto $P_{0} (0, - 1, 8) .$

De acuerdo con lo que hemos visto, tenemos toda la información para escribir la ecuación vectorial paramétrica:

$(x, y, z) = (0, - 1, 8) + α (3, - 1, 5) + β (7, 3, 2), c o n α, β \in R$

Nota: Para cada $α y β \in R$ se obtiene un punto del plano. Por ejemplo si $α = 1 y β = - 1$ se obtiene el punto $(x, y, z) = (- 4, - 5, 11)$ .

Busquemos ahora la ecuación general de este plano.

$\vec{n} = \vec{u} \times \vec{v} = (3, - 1, 5) \times (7, 3, 2) = (- 17, 29, 16)$

Luego:

$- 17 x + 29 y + 16 z + d = 0$

Reemplazamos $P_{0}$ para obtener $d$ :

$- 17.0 + 29. (- 1) + 16.8 + d = 0 \Rightarrow d = - 99$

Luego:

$- 17 x + 29 y + 16 z - 99 = 0$

que es la ecuación general o implícita del plano.

De la ecuación general a la ecuación vectorial paramétrica

Dada la ecuación general de un plano, ¿cómo puede obtenerse una ecuación vectorial paramétrica de dicho plano?

Consideremos el siguiente ejemplo:

$ω : 2 x - y + 3 z + 9 = 0$

Podemos despejar cualquiera de las variables, por ejemplo y:

$y = 2 x + 3 z + 9$

Entonces:

$ω : (x, y, z) = (x, 2 x + 3 z + 9, z)$

Reescribimos como suma de tres vectores, de forma tal que uno de ellos tenga los términos con $x$ , otro los términos con $z$ y otro los términos independientes:

$(x, y, z) = (x, 2 x, 0) + (0, 3 z, z) + (0, 9, 0)$

$(x, y, z) = x (1, 2, 0) + z (0, 3, 1) + (0, 9, 0), c o n x, z \in R$

Si llamamos $x = α$ , $z = β$ , resulta:

$ω : (x, y, z) = (0, 9, 0) + α (1, 2, 0) + β (0, 3, 1), c o n α, β \in R$

Obtuvimos así una ecuación vectorial paramétrica del plano $ω .$

El lector puede comprobar que: i) los vectores $\vec{u}$ = (1,2,0) y $\vec{v}$ = (0,3,1) son perpendiculares a $\vec{n}$ = (2,-1,3), o sea que son paralelos al plano; ii) P0(0,9,0) $\in ω$ .