Transformadas de Fourier

https://la.mathworks.com/help/matlab/math/fourier-transforms.html

La transformada de Fourier es una fórmula matemática que transforma una señal muestreada en tiempo o espacio con la misma señal muestreada en frecuencia temporal o espacial. En el procesamiento de señales, la transformada de Fourier puede revelar características importantes de una señal, es decir, sus componentes de frecuencia.

La transformada de Fourier se define para un vector x con puntos n muestreados uniformemente por

yk+1=n−1∑j=0ωjkxj+1.

ω=e−2πi/n es una de n raíces complejas de unidad donde i es la unidad imaginaria. Para x e y, los índices j y k oscilan entre 0 y n−1.

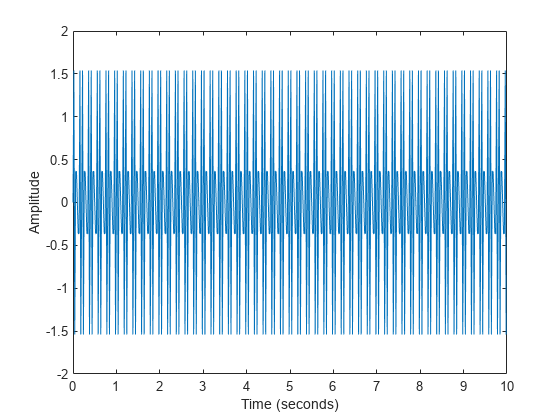
La función fft de MATLAB® utiliza un algoritmo de la transformada rápida de Fourier para calcular la transformada de Fourier de los datos. Considere una señal sinusoidal x que es una función de tiempo t con componentes de frecuencia de 15 Hz y 20 Hz. Utilice un vector de tiempo muestreado en incrementos de 1/50 segundos en un periodo de 10 segundos.

Ts = 1/50;
t = 0:Ts:10-Ts;
x = sin(2*pi*15*t) + sin(2*pi*20*t);
plot(t,x)
xlabel('Time (seconds)')
ylabel('Amplitude')

Calcule la transformada de Fourier de la señal y cree el vector f que se corresponde con el muestreo de la señal en el espacio de frecuencia.

y = fft(x);
fs = 1/Ts;
f = (0:length(y)-1)*fs/length(y);

Cuando representa la magnitud de la señal como una función de frecuencia, los picos de la magnitud se corresponden con los componentes de frecuencia de 15 Hz y 20 Hz de la señal.

plot(f,abs(y))
xlabel('Frequency (Hz)')
ylabel('Magnitude')
title('Magnitude')

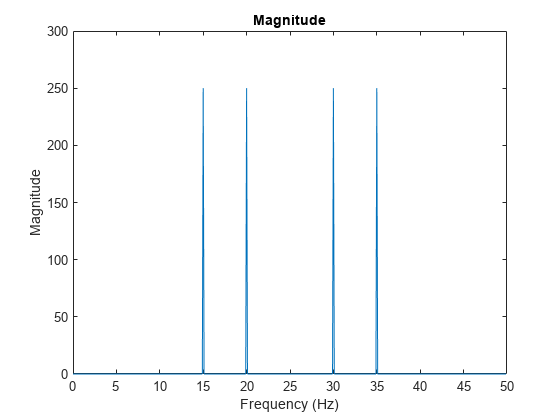
La transformada también genera una copia reflejada de los picos, que se corresponden con las frecuencias negativas de las señales. Para visualizar mejor esta periodicidad, puede utilizar la función fftshift, que realiza un desplazamiento circular y centrado en cero en la transformada.

n = length(x);
fshift = (-n/2:n/2-1)*(fs/n);
yshift = fftshift(y);
plot(fshift,abs(yshift))
xlabel('Frequency (Hz)')
ylabel('Magnitude')

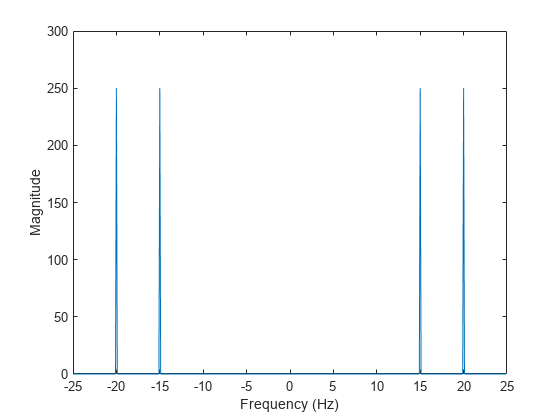
Señales sinusoidales

En aplicaciones científicas, las señales suelen corromperse debido a ruido aleatorio, lo que enmascara sus componentes de frecuencia. La transformada de Fourier puede procesar la separación del ruido aleatorio y revelar las frecuencias. Por ejemplo, cree una nueva señal, xnoise, inyectando ruido gaussiano en la señal original, x.

rng('default')
xnoise = x + 2.5*randn(size(t));

La potencia de la señal como una función de frecuencia es una métrica habitual utilizada en el procesamiento de señales. La potencia es la magnitud cuadrada de la transformada de Fourier de una señal, normalizada por el número de muestras de frecuencia. Calcule y represente el espectro de potencia de la señal de ruido centrada en la frecuencia cero. A pesar del ruido, podrá distinguir las frecuencias de la señal debido a los picos de potencia.

ynoise = fft(xnoise);
ynoiseshift = fftshift(ynoise);
power = abs(ynoiseshift).^2/n; 
plot(fshift,power)
title('Power')
xlabel('Frequency (Hz)')
ylabel('Power')

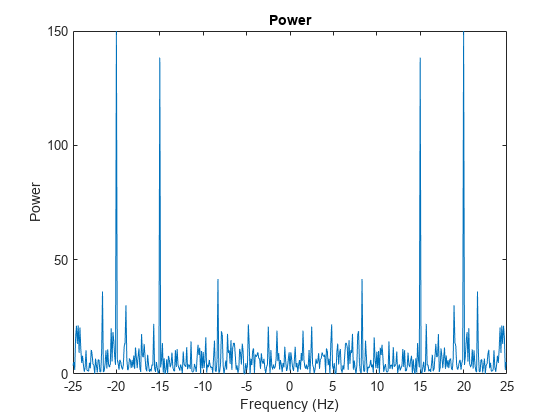
Eficiencia computacional

Utilizar la fórmula de la transformada de Fourier directamente para calcular cada uno de los elementos n de y requiere n2 operaciones en punto flotante. El algoritmo de la transformada rápida de Fourier solo requiere n log n operaciones para calcularse. Esta eficiencia computacional supone una gran ventaja al procesar datos con millones de puntos de datos. Muchas implementaciones especializadas del algoritmo de la transformada rápida de Fourier son incluso más eficientes cuando n tiene factores primos pequeños, como n es una potencia de 2.

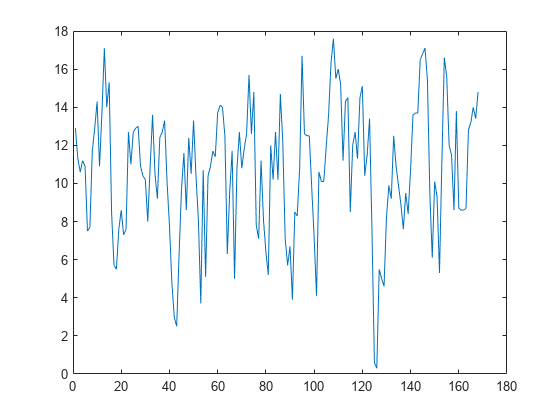
Considere los datos de audio recogidos por micrófonos submarinos en la costa de California. Estos datos se encuentran en una biblioteca del Programa de Investigación sobre Bioacústica de la Universidad de Cornell. Cargue y especifique el formato de un subconjunto de los datos de bluewhale.au, que contiene la vocalización de una ballena azul del Pacífico. Puesto que los sonidos de las ballenas azules son sonidos de baja frecuencia, son casi imperceptibles para los humanos. La escala de tiempo en los datos se comprime con un factor de 10 para aumentar el tono y hacer el sonido más perceptible. Puede utilizar el comando sound(x,fs) para escuchar el archivo de audio completo.

whaleFile = 'bluewhale.au';
[x,fs] = audioread(whaleFile);
whaleMoan = x(2.45e4:3.10e4);
t = 10*(0:1/fs:(length(whaleMoan)-1)/fs);

plot(t,whaleMoan)
xlabel('Time (seconds)')
ylabel('Amplitude')
xlim([0 t(end)])

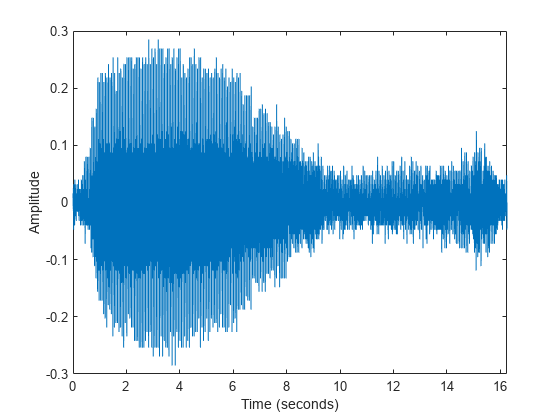
Especifique una nueva longitud de señal que sea la siguiente potencia de 2 superior a la longitud original. Después, utilice fft para calcular la transformada de Fourier utilizando la nueva longitud de señal. fft rellena automáticamente los datos con ceros para aumentar el tamaño de la muestra. Este relleno puede agilizar de forma significativa el cálculo de la transformada, especialmente para tamaños de muestras con factores primos grandes.

m = length(whaleMoan);
n = pow2(nextpow2(m));
y = fft(whaleMoan,n);

Represente el espectro de potencia de la señal. La gráfica indica que el gemido se compone de una frecuencia fundamental de aproximadamente 17 Hz y una secuencia de armónicos, donde se enfatiza el segundo armónico.

f = (0:n-1)*(fs/n)/10; % frequency vector
power = abs(y).^2/n;   % power spectrum
plot(f(1:floor(n/2)),power(1:floor(n/2)))
xlabel('Frequency (Hz)')
ylabel('Power')

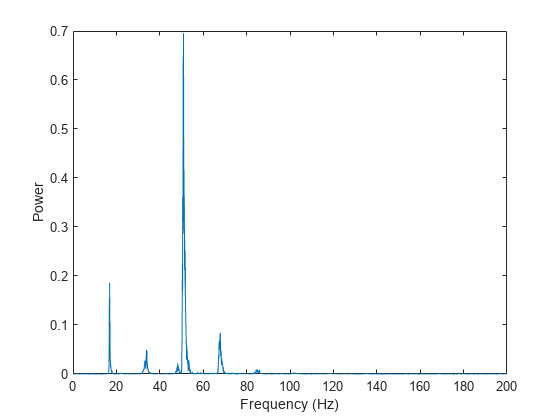
La fase de los sinusoides

Usando la transformada de Fourier, también puede extraer el espectro de fase de la señal original. Por ejemplo, cree una señal que conste de dos sinusoides con frecuencias de 15 Hz y 40 Hz. La primera sinusoide es una onda de coseno con fase −π/4 y la segunda es una onda de coseno con fase π/2. Muestree la señal a 100 Hz por 1 segundo.

fs = 100;
t = 0:1/fs:1-1/fs;
x = cos(2*pi*15*t - pi/4) - sin(2*pi*40*t);

Calcule la transformada de Fourier de la señal. Represente la magnitud de la transformada como una función de frecuencia.

y = fft(x);
z = fftshift(y);

ly = length(y);
f = (-ly/2:ly/2-1)/ly*fs;

stem(f,abs(z))
xlabel("Frequency (Hz)")
ylabel("|y|")
grid

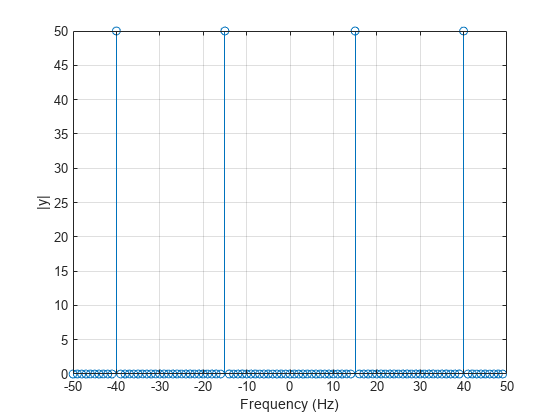
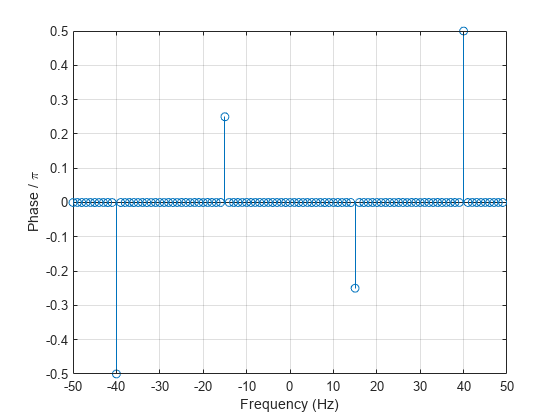
Calcule la fase de la transformada eliminando los valores de la transformada de magnitudes pequeñas. Represente la fase como una función de frecuencia.

tol = 1e-6;
z(abs(z) < tol) = 0;

theta = angle(z);

stem(f,theta/pi)
xlabel("Frequency (Hz)")
ylabel("Phase / \pi")
grid

Consulte también

fft | fftshift | nextpow2 | ifft | fft2 | fftn | fftw

Temas relacionados

• Transformadas de Fourier 2D

Sitios web externos

• Análisis de Fourier (recursos didácticos de MathWorks)

Ajustar modelos de Fourier

https://la.mathworks.com/help/curvefit/fourier.html

Ajustar modelos de Fourier

Sobre los modelos de serie de Fourier

Una serie de Fourier describe una función periódica como una suma de funciones de seno y coseno. Una función periódica arbitraria se puede descomponer en componentes simples mediante el uso de una serie de Fourier. Estos componentes son fáciles de integrar, diferenciar y analizar. Por esta razón, las series de Fourier se emplean con frecuencia para aproximar señales periódicas.

Las series de Fourier se representan con varios formatos. Curve Fitting Toolbox™ usa la serie de Fourier trigonométrica

y=a0+n∑i=1aicos(iwx)+bisin(iwx)

en la que a0 modela un término constante (intercepto) en los datos y se asocia con el término coseno i = 0, w es la frecuencia fundamental de la señal y n es el número de términos (armónicos). Curve Fitting Toolbox admite la regresión de series de Fourier para 1 ≤ n ≤ 8.

Para obtener más información sobre las series de Fourier, consulte Análisis y filtrado de Fourier.

Ajustar el modelo de Fourier de forma interactiva en la app Curve Fitter

En este ejemplo se muestra cómo utilizar la app Curve Fitter para ajustar un modelo de Fourier a los datos.

Cargue los datos de muestra de señal de sonido.

load gong.mat

Las variables y y Fs contienen datos de la señal de sonido y frecuencia para un sonido de gong, respectivamente. Cree un clip de sonido almacenando los primeros 1000 elementos de y en un vector denominado gongClip.

gongClip = y(1:1000);

Para calcular el tiempo correspondiente de cada elemento en gongClip, divida el índice de los elementos por Fs.

t = [1:1000]./Fs;

Abra la app Curve Fitter desde la línea de comandos.

curveFitter

También puede hacer clic en Curve Fitter dentro del grupo Math, Statistics and Optimization de la pestaña Apps.

En la app Curve Fitter, seleccione las variables de datos para el ajuste. En la sección Data de la pestaña Curve Fitter, haga clic en Select Data. En el cuadro de diálogo Select Fitting Data, seleccione t como el valor X data y gongClip como el valor Y data.

La app representa los puntos de datos a medida que selecciona variables. De forma predeterminada, la app ajusta un polinomio a los datos. Para ajustar un modelo de Fourier, en la sección Fit Type de la pestaña Curve Fitter, haga clic en Fourier.

La app se ajusta a un modelo de Fourier de un solo término.

El modelo de Fourier ajustado de un término es una función periódica con un comportamiento oscilatorio simple. En el panel Results se muestra la ecuación general para el modelo, las estimaciones de los coeficientes ajustados con intervalos de confianza del 95%, la frecuencia fundamental y las estadísticas de bondad de ajuste.

El modelo de Fourier ajustado de un término tiene un error cuadrático medio (RMSE) de 0,1996. Para comparar el modelo de Fourier de un término con un modelo de Fourier de cuatro términos, en el panel Fit Options, seleccione 4 para Number of terms. La app ajusta un modelo de Fourier de cuatro términos a los datos.

El modelo de Fourier ajustado de cuatro términos tiene un comportamiento oscilatorio más complejo que el modelo de Fourier de un término. Un RMSE de 0,1685 para el modelo de cuatro términos indica que cuatro términos predicen los datos de sonido con mayor precisión que uno solo. Sin embargo, la gráfica muestra que algunos de los puntos de datos de gongClip están fuera del rango del modelo de cuatro términos.

Exporte el modelo de Fourier ajustado de cuatro términos al área de trabajo haciendo clic en Export en la sección Export y, a continuación, seleccionando Export to Workspace. En el cuadro de diálogo, desmarque la segunda y la tercera opción. Guarde el ajuste en el nombre de la variable en el recuadro junto a la primera opción.

Puede escuchar los datos de sonido de gongClip utilizando la función sound.

sound(gongClip,Fs)
pause(2)    % Allow gongClip to play before executing next line

Para obtener los datos de sonido para la aproximación del modelo de Fourier de gongClip, use feval para evaluar gongFourierModel en los tiempos de t. Reproduzca los datos de sonido aproximados.

gongClipApprox = feval(gongFourierModel,t);
sound(gongClipApprox,Fs)

Los dos clips tienen el mismo tono promedio aproximado. Sin embargo, los datos de sonido aproximados no tienen tantas fluctuaciones de tono como los datos de sonido de gongClip.

Ajustar el modelo de Fourier en la línea de comandos

En este ejemplo se muestra cómo ajustar un modelo de Fourier a los datos empleando la función fit.

Ajustar modelos de Fourier de dos términos

Cargue los datos de El Niño-Southern Oscilation (ENSO).

load enso;

La variable pressure contiene datos para la diferencia de presión atmosférica promediada entre la Isla de Pascua, Chile, y Darwin, Australia. La variable month contiene datos del mes en que se produjo cada diferencia de presión.

Represente pressure contra month.

plot(month,pressure)

Los datos de presión oscilan entre 0 y 18, lo que indica que se pueden describir con una serie de Fourier.

Para ajustar un modelo de Fourier de dos términos, utilice el modelo de Fourier de la biblioteca. Especifique el tipo de modelo como fourier seguido del número de términos. Guarde los valores estadísticos de bondad de ajuste para compararlos más adelante.

[f2,gof2] = fit(month,pressure,"fourier2")

f2 = 
     General model Fourier2:
     f2(x) =  a0 + a1*cos(x*w) + b1*sin(x*w) + 
               a2*cos(2*x*w) + b2*sin(2*x*w)
     Coefficients (with 95% confidence bounds):
       a0 =       10.63  (10.23, 11.03)
       a1 =       2.923  (2.27, 3.576)
       b1 =       1.059  (0.01593, 2.101)
       a2 =     -0.5052  (-1.086, 0.07532)
       b2 =      0.2187  (-0.4202, 0.8576)
       w =      0.5258  (0.5222, 0.5294)

gof2 = struct with fields:
           sse: 1.1230e+03
       rsquare: 0.4279
           dfe: 162
    adjrsquare: 0.4103
          rmse: 2.6329

f2 es un objeto cfit que contiene la fórmula general, las estimaciones de coeficientes con límites de confianza del 95% y frecuencia fundamental para el ajuste w. Los límites de confianza en a2 y b2 cruzan por cero, por lo que no hay suficiente evidencia para concluir que difieren de cero o que el modelo ajustado difiere de un modelo de Fourier de un término. El error cuadrático medio (RMSE) de 2,6329 es útil para comparar la precisión de f2 con la precisión de otros ajustes.

Para calcular el periodo a partir de la frecuencia fundamental, utilice la fórmula T = 2*pi/w.

w = f2.w

w = 0.5258

T = 2*pi/w

T = 11.9497

El periodo del modelo de Fourier de dos términos ajustado es de aproximadamente 12 meses, o un año.

Represente f2 con una gráfica de dispersión de los datos.

plot(f2,month,pressure)

La forma de f2 es similar a la forma de un modelo de Fourier de un término, y los picos de oscilación se producen aproximadamente una vez cada 12 meses.

Ajustar modelos de Fourier de siete términos

Ajuste un modelo de Fourier de siete términos a los datos. Guarde las estadísticas de bondad de ajuste.

[f7,gof7] = fit(month,pressure,"fourier7")

f7 = 
     General model Fourier7:
     f7(x) = 
               a0 + a1*cos(x*w) + b1*sin(x*w) + 
               a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w) + 
               a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w) + 
               a6*cos(6*x*w) + b6*sin(6*x*w) + a7*cos(7*x*w) + b7*sin(7*x*w)
     Coefficients (with 95% confidence bounds):
       a0 =       10.63  (10.28, 10.97)
       a1 =      0.5669  (0.08285, 1.051)
       b1 =      0.1969  (-0.29, 0.6838)
       a2 =      -1.203  (-1.687, -0.7189)
       b2 =     -0.8085  (-1.307, -0.31)
       a3 =      0.9323  (0.4325, 1.432)
       b3 =      0.7599  (0.2622, 1.258)
       a4 =     -0.6653  (-1.149, -0.1817)
       b4 =     -0.2038  (-0.6995, 0.292)
       a5 =    -0.02913  (-0.5129, 0.4547)
       b5 =     -0.3701  (-0.8566, 0.1164)
       a6 =    -0.04841  (-0.5437, 0.4469)
       b6 =     -0.1367  (-0.6286, 0.3552)
       a7 =       2.812  (2.19, 3.433)
       b7 =       1.333  (0.4017, 2.264)
       w =     0.07527  (0.07478, 0.07576)

gof7 = struct with fields:
           sse: 768.3656
       rsquare: 0.6086
           dfe: 152
    adjrsquare: 0.5700
          rmse: 2.2483

f7 contiene varios coeficientes con límites de confianza que cruzan por cero, por lo que no hay suficiente evidencia para concluir que los términos correspondientes aumentan la precisión del modelo de Fourier ajustado. El RMSE de 2,2483 es menor que el error RMSE de f2, lo que confirma que el modelo de Fourier de siete términos predice la presión de manera más precisa que el modelo de Fourier de dos términos.

Para calcular el periodo a partir de la frecuencia fundamental, utilice la fórmula T = 2*pi/w.

w = f7.w

w = 0.0753

T = (2*pi)/w

T = 83.4745

El periodo del modelo de Fourier de 7 términos ajustado es de aproximadamente 83 meses, o aproximadamente 7 años. La amplitud de los coeficientes ajustados determina qué términos contribuyen más al valor previsto de la diferencia de presión.

El periodo de una sinusoide del formato sin(Ax) o cos(Ax) lo proporciona la fórmula T = 2*pi/|A|. a7 y b7 son los coeficientes más grandes.

T = 2*pi/(w*7)

T = 11.9249

El periodo de los términos correspondientes a a7 y b7 es de aproximadamente 12 meses, lo que indica que el ciclo anual es el más fuerte.

Use la misma fórmula para calcular los periodos de los términos siguientes:

• Los términos a1 y b1 tienen un periodo de 7 años cada uno.

• Los términos a2 y b2 tienen un periodo de 3,5 años (7/2) cada uno. Los coeficientes a2 y b2 tienen una magnitud mayor que a1 y b1, por lo que el ciclo de 3,5 años contribuye más al valor previsto de la diferencia de presión que el ciclo de 7 años.

• Los términos a3 y b3 son fuertes, lo que indica un ciclo de 2,3 años (7/3).

Los términos más pequeños, como a6, b6, a5 y b5, son menos importantes para el ajuste.

Represente f7 con una gráfica de dispersión de los datos.

plot(f7,month,pressure)

El modelo de Fourier de 7 términos oscila en un patrón más complejo y captura un rango más amplio de valores en la diferencia de presión que el modelo de Fourier de un solo término. El ciclo se repite aproximadamente cada 84 meses, o 7 años. Habitualmente, el calentamiento de El Niño se produce en intervalos irregulares de entre dos y siete años, y dura entre 9 meses y 2 años. La duración media del periodo es de cinco años. Los resultados del modelo reflejan algunos de estos periodos.

Definir los puntos de partida

La función fit utiliza el argumento de entrada data para calcular los puntos de partida optimizados de los cálculos del coeficiente y la frecuencia fundamental. Los modelos de serie de Fourier son especialmente sensibles a los puntos de partida y es posible que los valores optimizados sean precisos solo para algunos términos en las ecuaciones asociadas. Puede anular los puntos de partida optimizados especificando el argumento nombre-valor StartPoint.

Los valores extremos en la gráfica de dispersión de los datos sugieren que puede estar presente un ciclo de 4 años. Para confirmar esta sugerencia, establezca el punto de partida de la frecuencia fundamental en el valor correspondiente a un periodo de 8 años, o 96 meses. Un periodo de 8 años para el modelo de Fourier ajustado aumenta el periodo de los términos a2 y b2 de 3.5 a 4.

w_8 = (2*pi)/96

w_8 = 0.0654

Para encontrar el índice de la frecuencia fundamental en el vector de celdas de nombres de coeficientes de f7, utilice la función coeffnames.

coeffnames(f7)

ans = 16×1 cell
    {'a0'}
    {'a1'}
    {'b1'}
    {'a2'}
    {'b2'}
    {'a3'}
    {'b3'}
    {'a4'}
    {'b4'}
    {'a5'}
    {'b5'}
    {'a6'}
    {'b6'}
    {'a7'}
    {'b7'}
    {'w' }

La frecuencia fundamental se encuentra en la última entrada del vector de nombres de coeficientes. Cree un vector de valores de coeficientes a partir de los coeficientes f7 y sustituya el valor de la frecuencia fundamental con el valor correspondiente a un periodo de 8 años.

coeffs = coeffvalues(f7);
coeffs(:,end) = w_8

coeffs = 1×16

   10.6262    0.5669    0.1969   -1.2031   -0.8085    0.9323    0.7599   -0.6653   -0.2038   -0.0291   -0.3701   -0.0484   -0.1367    2.8120    1.3330    0.0654

Ajuste un modelo de Fourier de siete términos a los datos de la diferencia de presión utilizando los coeficientes con el nuevo valor de la frecuencia fundamental como punto de partida. Guarde las estadísticas de bondad de ajuste.

[f7_8,gof7_8] = fit(month,pressure,"fourier7",StartPoint=coeffs)

f7_8 = 
     General model Fourier7:
     f7_8(x) = 
               a0 + a1*cos(x*w) + b1*sin(x*w) + 
               a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w) + 
               a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w) + 
               a6*cos(6*x*w) + b6*sin(6*x*w) + a7*cos(7*x*w) + b7*sin(7*x*w)
     Coefficients (with 95% confidence bounds):
       a0 =       10.58  (10.05, 11.1)
       a1 =      0.3286  (-0.4339, 1.091)
       b1 =    -0.05917  (-0.7884, 0.6701)
       a2 =     -0.8667  (-1.738, 0.004258)
       b2 =       1.094  (0.2819, 1.906)
       a3 =     -0.4524  (-1.232, 0.3272)
       b3 =     -0.3117  (-1.099, 0.4753)
       a4 =       0.181  (-0.7949, 1.157)
       b4 =      0.5806  (-0.1796, 1.341)
       a5 =     0.03263  (-0.7174, 0.7827)
       b5 =     -0.2299  (-0.9767, 0.5169)
       a6 =      0.3726  (-0.39, 1.135)
       b6 =     -0.2745  (-1.165, 0.6161)
       a7 =      0.4309  (-0.491, 1.353)
       b7 =     -0.3547  (-1.316, 0.6062)
       w =     0.06795  (0.06519, 0.0707)

gof7_8 = struct with fields:
           sse: 1.6851e+03
       rsquare: 0.1416
           dfe: 152
    adjrsquare: 0.0568
          rmse: 3.3296

Los coeficientes de f7_8 están ligeramente desplazados con respecto a los coeficientes de f7. La RMSE más alta para f7_8 indica que f7 es un mejor ajuste para los datos. Represente ambos ajustes para comparar los modelos visualmente.

plot(f7_8,month,pressure)
hold on
plot(f7, 'b')
hold off
legend("Data","f7_8","f7")

La gráfica muestra que f7 captura la variación de los datos de la diferencia de presión de forma más precisa que f7_8.

Mostrar iteraciones de ajuste de Fourier

Una alternativa a especificar opciones adicionales mediante argumentos de par nombre-valor es pasar un objeto fitoptions a la función fit. Para ver las opciones disponibles para un ajuste del modelo de Fourier, pase el nombre del modelo como argumento de entrada a la función fitoptions.

fitoptions("fourier7")

ans =

        Normalize: 'off'
          Exclude: []
          Weights: []
           Method: 'NonlinearLeastSquares'
           Robust: 'Off'
       StartPoint: [1×0 double]
            Lower: [1×0 double]
            Upper: [1×0 double]
        Algorithm: 'Trust-Region'
    DiffMinChange: 1.0000e-08
    DiffMaxChange: 0.1000
          Display: 'Notify'
      MaxFunEvals: 600
          MaxIter: 400
           TolFun: 1.0000e-06
             TolX: 1.0000e-06

Cree un objeto fitoptions y especifique que se muestre la salida tras cada iteración.

optionsf7 = fitoptions("fourier7",Display="iter")

options =

        Normalize: 'off'
          Exclude: []
          Weights: []
           Method: 'NonlinearLeastSquares'
           Robust: 'Off'
       StartPoint: [1×0 double]
            Lower: [1×0 double]
            Upper: [1×0 double]
        Algorithm: 'Trust-Region'
    DiffMinChange: 1.0000e-08
    DiffMaxChange: 0.1000
          Display: 'Iter'
      MaxFunEvals: 600
          MaxIter: 400
           TolFun: 1.0000e-06
             TolX: 1.0000e-06

optionsf7 es un objeto fitoptions que contiene las opciones de un ajuste de modelo de Fourier de 7 términos.

Para ver los pasos de iteración involucrados en la creación de f7, ajuste otro modelo de Fourier de 7 términos usando las opciones de optionsf7.

f7_iter = fit(month,pressure,"fourier7",optionsf7)

                                         Norm of      First-order 
 Iteration  Func-count     f(x)          step          optimality   CG-iterations
     0          2          768.41                      1.93e+03
     1          4         768.366     2.2176e-05           69.1            0
     2          6         768.366    7.94962e-07           2.48            0
Success, but fitting stopped because change in residuals less than tolerance (TolFun).

f7_iter = 
     General model Fourier7:
     f7_iter(x) = 
               a0 + a1*cos(x*w) + b1*sin(x*w) + 
               a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w) + 
               a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w) + 
               a6*cos(6*x*w) + b6*sin(6*x*w) + a7*cos(7*x*w) + b7*sin(7*x*w)
     Coefficients (with 95% confidence bounds):
       a0 =       10.63  (10.28, 10.97)
       a1 =      0.5669  (0.08285, 1.051)
       b1 =      0.1969  (-0.29, 0.6838)
       a2 =      -1.203  (-1.687, -0.7189)
       b2 =     -0.8085  (-1.307, -0.31)
       a3 =      0.9323  (0.4325, 1.432)
       b3 =      0.7599  (0.2622, 1.258)
       a4 =     -0.6653  (-1.149, -0.1817)
       b4 =     -0.2038  (-0.6995, 0.292)
       a5 =    -0.02913  (-0.5129, 0.4547)
       b5 =     -0.3701  (-0.8566, 0.1164)
       a6 =    -0.04841  (-0.5437, 0.4469)
       b6 =     -0.1367  (-0.6286, 0.3552)
       a7 =       2.812  (2.19, 3.433)
       b7 =       1.333  (0.4017, 2.264)
       w =     0.07527  (0.07478, 0.07576)

Para investigar más el ajuste del modelo de Fourier, puede experimentar especificando diferentes opciones disponibles para el algoritmo de ajuste de NonlinearLeastSquares. Para obtener más información, consulte fitoptions.

Consulte también

Apps

• Curve Fitter

Funciones

• fit | fittype | fitoptions