La construcción de la escala musical, Construcción de las notas

http://www.xtec.cat/centres/a8019411/caixa/escalas.htm

La construcción de la escala musical En este apartado, expondremos los orígenes de la escala musical que utilizamos en occidente. Esta escala ha ido variando con los años, y la actual es fruto de convenios, pero tiene un importante origen en las propiedades físicas.  Las matemáticas tienen también gran importancia en sus orígenes y su posterior evolución. Explicaremos como se construye la escala musical a partir de proporciones de las frecuencias de las diferentes notas a partir de una nota dada. Y también, como esto ha dado problemas para fijar una escala definitiva a gusto de todos.     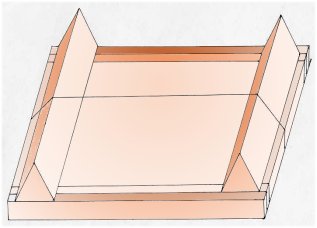[El origen de la escala musical | La construcción de la escala musical] El origen de la escala musical La escala actual (escala occidental) es el resultado de un largo proceso de aprendizaje de las notas. Los pitagóricos construyeron un aparato llamado monocordio que se componía de una tabla, una cuerda tensa y una tabla más pequeña que se iba moviendo por la grande.    Monocordio Los pitagóricos observaron que haciendo más o menos larga la cuerda (moviendo la tabla móvil) se producían sonidos diferentes. Entre estos sonidos escogieron algunos que eran armoniosos con el sonido original (cuerda entera). Los más importantes, por su simplicidad y su importancia a la hora de construir la escala musical, són: La octava. Cuando la cuerda medía un medio del total, el sonido se repetía, pero más agudo. La octava es lo que correspondería a un salto de ocho teclas blancas del piano; o mejor dicho, una octava es la repetición de un sonido con una cuerda con la mitad de largura, por tanto, otra nota armoniosa. Su frecuencia es doble. La quinta es otro intervalo entre notas que se obtiene con una cuerda de largura dos tercios de la inicial. Su frecuencia es de tres medios del sonido inicial. Corresponde a un salto de cinco teclas blancas en un piano. La cuarta es, como las anteriores, otro intervalo entre notas que se obtiene con una cuerda de largura tres cuartos de la inicial. Su frecuencia es cuatro tercios de la nota inicial. Así, a partir de un sonido original obtenemos diferentes notas armoniosas. Haciendo un pequeño esquema nos aclararemos más:  Nota Frecuencia Long. cuerda Original  F L Octava 2f 1/2·L Quinta 3/2·f 2/3·L Cuarta 4/3·f 3/4·L Si suponemos que la nota inicial es el do, entonces la octava, quinta y cuarta són las notas:  Nota base  Cuarta Quinta Octava  Do  Fa  Sol  Do (1 octava más alta)  Que corresponden a la cuarta, quinta y octava notas respectivamente de la escala diatónica (las teclas blancas del piano). Todas estas relaciones entre las notas se denominan intervalos. La construcción de la escala musical Pero, ¿cómo se pueden encontrar las notas de nuestra escala musical a partir de una nota base (tónica)?. Vamos a hacer un proceso repetitivo a partir de esta nota, utilizando las quintas y las octavas. Lo que queremos hacer es encontrar notas armoniosas con la nota base que se encuentren entre la nota original y su octava. Supondremos que la nota original tiene una frecuencia f. Entonces, la octava tendrá frecuencia 2f. Queremos encontrar notas que tengan frecuencia entre f y 2f La primera que tenemos es la quinta, la frecuencia es 3/2·f. Corresponde a una cuerda de longitud 2/3 la inicial. El siguiente paso es encontrar la quinta de la quinta. La frecuencia será 3/2·3/2 ·f=9/4·f. El problema es que esa nota tiene una frecuencia más grande que 2f. Lo que hacemos es encontrar una nota una octava más abajo. Es decir, una nota con frecuencia 9/8·f. Si vamos repitiendo el proceso obtenemos las notas siguientes: f 3/2·f 9/8 ·f. Después de haber descendido una octava. 3/2·9/8 ·f=27/16·f 3/2·27/16 ·f=81/32·f. Como la frecuencia es más grande que 2f, descendemos una octava y obtenemos 81/64·f 3/2·81/64 ·f=243/128·f Hemos obtenido 7 notas, contando la octava, que podemos ordenar de frecuencia más pequeña a más grande de la forma siguiente:  Nota Base  f   9/8·f   81/64 ·f Quinta  3/2·f   27/16·f   243/128·f Octava  2·f De esta forma hemos obtenido 6 notas dentro de una octava. Pero si nos fijamos en la razón de frecuencias de una nota y la anterior,  (9/8):1=9/8 1,125 (81/64):(9/8)=9/8 1,125 (3/2):(81/64=32/27 1,185 (27/16):(3/2)=9/8  1,125 (243/128):(27/16)=9/8 1,125 2:(243/128)=256/243 1,053 parece que hay un agujero entre 81/64·f y 3/2·f. Curiosamente entre estos dos valores se encuentra 4/3·f, que corresponde a lo que hemos llamado cuarta. Añadiendo la cuarta, nos queda una escala de 7 notas con estas razones entre las frecuencias:    Frecuencia  Razón nota anterior    Tónica F   Do Segunda  9/8·f 9/8=1,125  Re Tercera 81/64·f 9/8=1,125 Mi  Cuarta 4/3·f 256/243=1,053 Fa Quinta  3/2·f 9/8=1,125 Sol  Sexta  27/16·f 9/8=1,125 La  Séptima  243/128·f 9/8=1,125 Si  Octava 2f 256/243=1,053  Do En la columna de la derecha hemos puesto el nombre de la nota que correspondería si la nota base fuese el do.  Esta es la escala que llamamos diatónica. Consta de 7 notas, la octava es la misma que la anterior una octava más alta. Se corresponden a las teclas blancas del piano. Podemos ver que hay dos razones diferentes: el tono 9/8 y el semitono 256/243. La pregunta que nos hacemos es qué relación hay entre las dos razones. Se puede ver que dos semitonos hacen casi un tono (256/243)2 =1,109, pero no es exactamente el mismo. Si ahora utilizásemos las cuartas para ir encontrando nuevas notas armoniosas, comenzarían a salir las "teclas negras" del piano, es decir, los sostenidos y los bemoles. Cuando la escala queda completa con 12 notas (las teclas negras y las blancas), esto es lo que se llama la escala.cromática     Como un tono no es exactamente dos semitonos, había lugares donde los intervalos eran más grandes o más pequeños que en otros lugares. Esto daba problemas para afinar instrumentos con intervalos fijos como el piano o la guitarra. Es para esto que se creó la escala temperada. La cantidad de notas que tiene es la misma, pero la forma de afinación es diferente. En la escala temperada, la razón entre la frecuencia de una nota y la anterior es siempre constante. Si llamamos r a esta razón, se cumplirá que las frecuencias formaran una progresión geométrica del tipo: f, f·r, f· r2, f·r3, f·r4, ..., f·r12 = 2·f de lo que se deduce que r12 = 2, de donde r =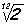 = 1,059... Esta escala resuelve los problemas de afinación, pero no podemos olvidar que las notas más armoniosas eran las que se había encontrado mediante el método geométrico, es decir las de la escala cromática. Instrumentos sin intervalos fijos como violines, contrabajos, etc. pueden utilizar la afinación de la escala cromática.