Transitorio analisis en el tiempo Transient Circuits RL RC RLC Differential equations solution step by step very nice solution
http://www.intmath.com/differential-equations/5-rl-circuits.php

Application of Ordinary Differential Equations: Series RL Circuit

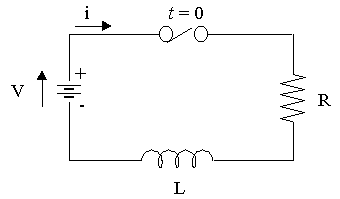
RL circuit diagram

The RL circuit shown above has a resistor and an inductor connected in series. A constant voltage V is applied when the switch is closed.
The (variable) voltage across the resistor is given by:

$\displaystyle{V}_{{R}}={i}{R}$

On this page...

Time constant
Two-mesh circuits
RL circuit examples
Two-mesh circuits

The (variable) voltage across the inductor is given by:

$\displaystyle{V}_{{L}}={L}\frac{{{d}{i}}}{{{\left.{d}{t}\right.}}}$

Kirchhoff's voltage law says that the directed sum of the voltages around a circuit must be zero. This results in the following differential equation:

$\displaystyle{R}{i}+{L}\frac{{{d}{i}}}{{{\left.{d}{t}\right.}}}={V}$

Once the switch is closed, the current in the circuit is not constant. Instead, it will build up from zero to some steady state.

Continues below ⇩

Solving the DE for a Series RL Circuit

The solution of the differential equation

\displaystyle{R}{i}+{L}\frac{{{d}{i}}}{{{\left.{d}{t}\right.}}}={V}

is:

$\displaystyle{i}=\frac{V}{{R}}{\left({1}-{e}^{{-{\left({R}\text{/}{L}\right)}{t}}}\right)}$

Proof

We start with:

$\displaystyle{R}{i}+{L}\frac{{{d}{i}}}{{{\left.{d}{t}\right.}}}={V}$

Subtracting Ri from both sides:

$\displaystyle{L}\frac{{{d}{i}}}{{{\left.{d}{t}\right.}}}={V}-{R}{i}$

Divide both sides by L:

$\displaystyle\frac{{{d}{i}}}{{{\left.{d}{t}\right.}}}=\frac{{{V}-{R}{i}}}{{L}}$

Multiply both sides by dt and divide both by (V - Ri):

$\displaystyle\frac{{{d}{i}}}{{{V}-{R}{i}}}=\frac{{{\left.{d}{t}\right.}}}{{L}}$

Integrate (see Integration: Basic Logarithm Form):

$\displaystyle\int\frac{{{d}{i}}}{{{V}-{R}{i}}}=\int\frac{{{\left.{d}{t}\right.}}}{{L}}$
$\displaystyle-\frac{{ \ln{{\left({V}-{R}{i}\right)}}}}{{R}}=\frac{1}{{L}}{t}+{K}$

Now, since

\displaystyle{i}={0}

when

\displaystyle{t}={0}

, we have:

$\displaystyle{K}=-\frac{{ \ln{\ }{V}}}{{R}}$

Substituting K back into our expression:

$\displaystyle-\frac{{ \ln{{\left({V}-{R}{i}\right)}}}}{{R}}=\frac{1}{{L}}{t}-\frac{{ \ln{{V}}}}{{R}}$

Rearranging:

$\displaystyle\frac{{ \ln{\ }{V}}}{{R}}-\frac{{ \ln{{\left({V}-{R}{i}\right)}}}}{{R}}=\frac{1}{{L}}{t}$

Multiplying throughout by -R:

$\displaystyle- \ln{\ }{V}+ \ln{{\left({V}-{R}{i}\right)}}=-\frac{R}{{L}}{t}$

Collecting the logarithm parts together:

$\displaystyle \ln{{\left(\frac{{{V}-{R}{i}}}{{V}}\right)}}=-\frac{R}{{L}}{t}$

Taking "e to both sides":

$\displaystyle\frac{{{V}-{R}{i}}}{{V}}={e}^{{-{\left({R}\text{/}{L}\right)}{t}}}$
$\displaystyle{1}-\frac{R}{{V}}{i}={e}^{{-{\left({R}\text{/}{L}\right)}{t}}}$

Subtracting 1 from both sides:

$\displaystyle-\frac{R}{{V}}{i}=-{1}+{e}^{{-{\left({R}\text{/}{L}\right)}{t}}}$

Multiplying both sides by

\displaystyle-{\left(\frac{V}{{R}}\right)}

$\displaystyle{i}=\frac{V}{{R}}{\left({1}-{e}^{{-{\left({R}\text{/}{L}\right)}{t}}}\right)}$

Please support IntMath!

[We did the same problem but with particular values back in section 2. Separation of Variables]

Here is the graph of this equation:

\displaystyle\frac{V}{{R}}

Graph of

\displaystyle{i}=\frac{V}{{R}}{\left({1}-{e}^{{-{\left({R}\text{/}{L}\right)}{t}}}\right)}

The plot shows the transition period during which the current adjusts from its initial value of zero to the final value

\displaystyle\frac{V}{{R}}

, which is the steady state.

The Time Constant

The time constant (TC), known as τ, of the function

$\displaystyle{i}=\frac{V}{{R}}{\left({1}-{e}^{{-{\left({R}\text{/}{L}\right)}{t}}}\right)}$

is the time at which

\displaystyle\frac{R}{{L}}

is unity ( = 1). Thus for the RL transient, the time constant is

\displaystyle\tau=\frac{L}{{R}}

seconds.
NOTE: τ is the Greek letter "tau" and is not the same as T or the time variable t, even though it looks very similar.
At 1 τ

\displaystyle{1}-{e}^{{-{\left({R}\text{/}{L}\right)}{t}}}

$\displaystyle={1}-{e}^{ -{{1}}}$
$\displaystyle={1}-{0.368}$
$\displaystyle={0.632}$

At this time the current is 63.2% of its final value.
Similarly at 2 τ,

$\displaystyle{1}-{e}^{ -{{2}}}={1}-{0.135}={0.865}$

The current is 86.5% of its final value.
After 5 τ the transient is generally regarded as terminated. For convenience, the time constant τ is the unit used to plot the current of the equation

$\displaystyle{i}=\frac{V}{{R}}{\left({1}-{e}^{{-{\left({R}\text{/}{L}\right)}{t}}}\right)}$

That is, since

\displaystyle\tau=\frac{L}{{R}}

, we think of it as:

$\displaystyle{i}=\frac{V}{{R}}{\left({1}-{e}^{{-{t}\text{/}\tau}}\right)}$

Let's now look at some examples of RL circuits.

Example 1

An RL circuit has an emf of 5 V, a resistance of 50 Ω, an inductance of 1 H, and no initial current.
Find the current in the circuit at any time t. Distinguish between the transient and steady-state current.

Show answer

Example 2

A series RL circuit with R = 50 Ω and L = 10 H has a constant voltage V = 100 V applied at t = 0 by the closing of a switch.
Find

(a) the equation for i (you may use the formula rather than DE),
(b) the current at t = 0.5 s
(c) the expressions for V_R and V_L
(d) the time at which V_R = V_L

Show answer

Two-mesh Circuits

The next two examples are "two-mesh" types where the differential equations become more sophisticated. We will use Scientific Notebook to do the grunt work once we have set up the correct equations.

Example 3

In the two-mesh network shown below, the switch is closed at t = 0 and the voltage source is given by V = 150 sin 1000t V. Find the mesh currents i₁ and i₂ as given in the diagram.

Show answer

Example 4

The switch is closed at t = 0 in the two-mesh network shown below. The voltage source is given by V = 30 sin 100t V. Find the mesh currents i₁ and i₂ as given in the diagram.