Baricentro en geometría analítica

Teorema:

Sea $ABC$ un triángulo cualquiera de vértices $(x_1,y_1)$ , $(x_2,y_2)$ y $(x_3,y_3)$ , entonces su baricentro (punto de trisección de las medianas) tiene como coordenada:

$G=(\tfrac{x_1+x_2+x_3}{3};\tfrac{y_1+y_2+y_3}{3})$

Demostración:

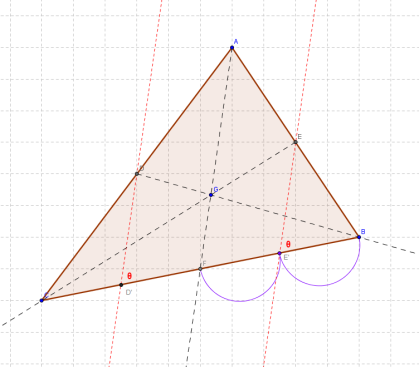
Sea ΔABC un triángulo cualquiera donde $A=(x_1, y_1), B=(x_2, y_2), C=(x_3, y_3)$ , si trazamos el punto medio a cada uno de los lados AC, AB y CB usamos la fórmula $D=(\tfrac{x_1+x_3}{2};\tfrac{y_1+y_3}{2})$ , $E=(\tfrac{x_1+x_2}{2};\tfrac{y_1+y_2}{2})$ y $F=(\tfrac{x_2+x_3}{2};\tfrac{y_3+y_2}{2})$ respectivamente. Baricentro

Si trazamos una recta paralela a una de las medianas (segmento desde el vértice hasta el punto medio opuesto) en este caso a $AF$ , tenemos que desde el punto E’ -que es nuevamente la mitad del punto medio del segmento $CB$ – hasta el punto E, forman un segmento que corta a $GB$ , de la misma manera el segmento $DD'$ . Por el teorema de Tales vemos que $2\tfrac{DG}{D'F}=\tfrac{GB}{FB}$ , entonces podemos apreciar que $2DG=GB$ . De forma análoga se demuestran que cumplen también para $AF$ y $CE$ .