|
|
 Equilibria and the Phase Line
Equilibria and the Phase Line

Solving a differential equation can be done in three major ways: analytical, qualitative, and numerical. We have seen some examples of differential equations solved through analytical techniques (for example: linear, separable, and Bernoulli equations). Euler's Method (though very primitive) illustrates the use of numerical techniques in solving differential equations. For the qualitative approach, we have defined the slope field of a differential equation and showed how this can be helpful when other techniques fail.
When the differential equation is autonomous, more can be said about the solutions using qualitative techniques.
Consider the autonomous differential equation
where f(y) is a function. Clearly we recognize a separable equation. So we know how to solve it via the analytical technique. First we look for the constant solutions as the roots of the equation
Then to find the nonconstant solutions we separate the variable
and integrate
Note that the integration may be hard if not impossible to carry out. So it may not be possible to use the analytical technique.
In this case, one may try numerical techniques. Unfortunately, numerical techniques fail if f(y) contains a parameter and we need to make conclusions relative to this parameter. For example, recall the logistic equation with harvesting (with a constant rate H)
where y(t) is the population of the given species at time t. In order to find the optimal rate H (which makes hunters happy as well as ecologists worried about preserving the species), numerical techniques may not be the best tool to use. Here we will see how new ideas based on a graphical approach will help us to say something about the solutions. Be aware that these ideas are only valid for autonomous equations.
Equilibria of Autonomous Equations
Consider the autonomous equation
The equilibria or constant solutions of this differential equation are the roots of the equation
Using the existence and uniqueness theorem, these constant solutions will cut the entire plane (where the solutions live) into independent regions. This means, if an initial condition belongs to one of the regions, then the solution satisfying the initial condition will stay in that region all the time.
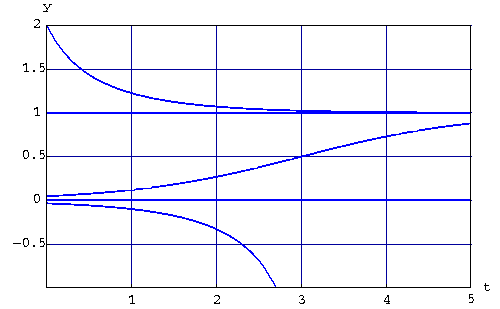
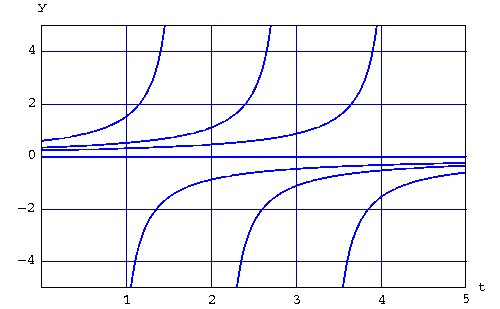
Example. Consider the logistic equation
Its equilibria are y=0 and y=1. Consider the solution y(t) to the IVP
Since 0 <y(0) < 1, then we must have
In the next picture, we draw few solutions associated to initial conditions in the different regions (0 < y < 1, y < 0, and 1 < y)
|
Assume that
where
we must have
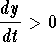 for all t. This
clearly implies that y(t) is always increasing. So the sign of
f(y) helps us determine the behavior of the solutions (whether they are
increasing or decreasing).
for all t. This
clearly implies that y(t) is always increasing. So the sign of
f(y) helps us determine the behavior of the solutions (whether they are
increasing or decreasing). Example. Consider the autonomous equation
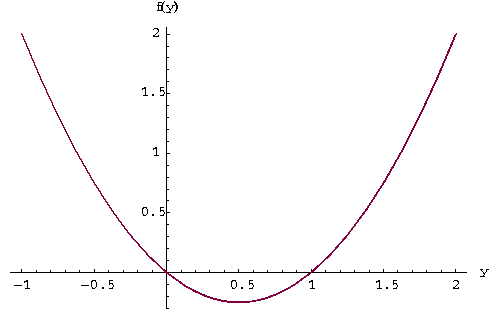
where the graph of f(y) is given below
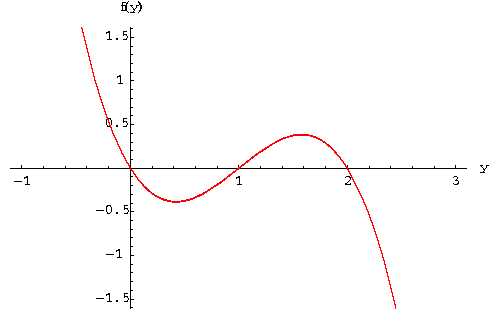
|
-

- if y(t) is a solution satisfying y(0) < 0, then y(t) is always increasing;
-

- if y(t) is a solution satisfying 0<y(0) < 1, then y(t) is always decreasing;
-

- if y(t) is a solution satisfying 1 <y(0) < 2, then y(t) is always increasing;
-

- if y(t) is a solution satisfying 2 <y(0), then y(t) is always decreasing.
|
-

- the limit of h(t) when
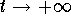 exists (or is a number) if and only if the function is bounded above; otherwise we have
exists (or is a number) if and only if the function is bounded above; otherwise we have

-

- the limit of h(t) when
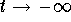 exists (or is a number) if and only if the function is bounded below; otherwise we have
exists (or is a number) if and only if the function is bounded below; otherwise we have

The next image illustrates this conclusion better than words can do.
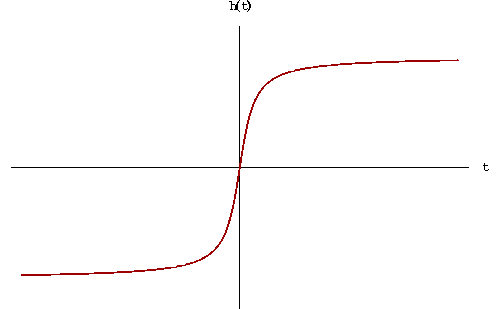
|
where the graph of f(y) is given below
|
Answer. Using the above results, we know that for the given initial condition, y(t) is decreasing and for every t we have
The above remark implies that
Since y(t) is not a constant solution (because y(0)=0.5), then we have
On the other hand, since
and y is solution to the autonomous equation y'=f(y), then the only possibilities for both limits are the equilibria 0,1, and 2. Clearly if we put everything together, we conclude that
|
- Step 1. Find the constant solutions or equilibria through the algebraic equation

Draw the constant solutions. Note that here we are drawing y versus t. - Step 2. Find the sign of the function f(y) through its graph (versus y).
- Step 3. In the region between any two equilibria, the solutions will be all increasing (if f(y) is positive) or decreasing (if f(y) is negative).
- Step 4. If a solution is increasing and bounded above by a constant solution y = L, then the limit of the solution when
 is the number L. Otherwise the limit is
is the number L. Otherwise the limit is  .
.
If this solution is bounded below by a constant solution y = l, then the limit of the solution when is the number l. Otherwise the limit is
is the number l. Otherwise the limit is 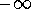 .
.
- Step 5. If a solution is decreasing and bounded below by a constant solution y = L, then the limit of the solution when
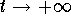 is the number L. Otherwise the limit is
is the number L. Otherwise the limit is 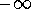 .
.
If this solution is bounded above by a constant solution y = l, then the limit of the solution when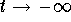 is the number l. Otherwise the limit is
is the number l. Otherwise the limit is  .
.
- Step 6. Draw some solutions.
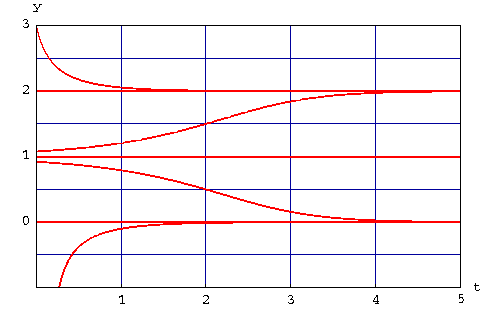
Example. Draw some solutions for the equation
Answer. Note that this equation models the logistic growth with threshold. The equilibria or constant solutions are given by
or y=0, y=2, and y=5. The graph of the function f(y) = .2y(5-y)(y-2) is given in the next picture
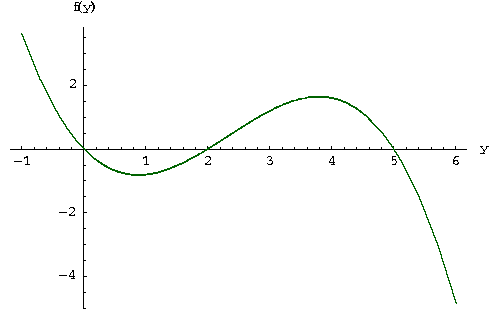
|
-

- the solution which satisfies the initial condition
 , with
, with  , is increasing. Moreover we have
, is increasing. Moreover we have

-

- the solution which satisfies the initial condition
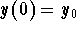 , with
, with 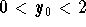 , is decreasing. Moreover we have
, is decreasing. Moreover we have
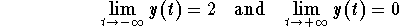
-

- the solution which satisfies the initial condition
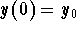 , with
, with 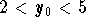 , is increasing. Moreover we have
, is increasing. Moreover we have
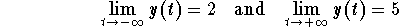
-

- the solution which satisfies the initial condition
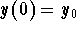 , with
, with 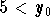 , is decreasing. Moreover we have
, is decreasing. Moreover we have
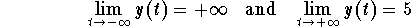

|
Let us reconsider the above example. Let us focus our attention on the solutions which satisfy the initial condition
It is somehow amazing that this conclusion is valid regardless whether
Definition. Classification of Equilibrium Points.
Consider the autonomous equation
Assume that
-

- The equilibrium point
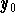 is called a sink
if and only if any solution y(t) to the autonomous equation such
that y(0) is close to
is called a sink
if and only if any solution y(t) to the autonomous equation such
that y(0) is close to 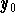 , then we have
, then we have

-

- The equilibrium point
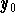 is called a source
if and only if any solution y(t) to the autonomous equation such
that y(0) is (or not) close to
is called a source
if and only if any solution y(t) to the autonomous equation such
that y(0) is (or not) close to 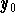 , then y(t) will move away from
, then y(t) will move away from
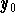 when
when 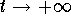 .
.
-

- The equilibrium point
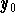 is called a node
if and only if it is neither a source nor a sink.
is called a node
if and only if it is neither a source nor a sink.
as source, sink, or node.
Answer. The equilibrium points are 0, 2, and 5. Using the above results, we see that 0 and 5 are sinks while 2 is a source.
Example. Find and classify the equilibrium points of the equation
as source, sink, or node.
Answer. It is easy to see that the only equilibrium point is 0. Since
-

- if y(t) is a solution satisfying y(0) < 0, then
we have

-

- if y(t) is a solution satisfying y(0) > 0, then
we have

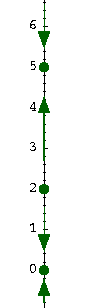
|
on the y-axis.
Then using the sign of f(y), we draw arrows pointing upward in a region where f(y) is positive, and downward in a region where f(y) is negative. This vertical line is called the phase line of the equation.
An equilibrium point is a sink, if the arrows on both sides point towards the equilibrium point, and it is a source, if both arrows point away from it.
Example. Draw the phase line of the equations
and
Answer. We will use our previous knowledge to get the two phase lines
|
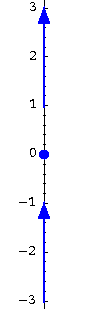
|
You can readily see, that an equilibrium point is a sink, if the arrows on both sides point towards the equilibrium point, and that it is a source, if both arrows point away from it.

 S.O.S. MATHematics home page
S.O.S. MATHematics home page 
Last Update 6-22-98
|
|
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
1231 users online during the last hour
No hay comentarios:
Publicar un comentario