| Hay
tres números irracionales cuyas aplicaciones, tanto en matemáticas
como en otras disciplinas, son tan numerosas e importantes que podríamos
denominarlos como los irracionales más famosos. Son
los números p (pi),
e, f (fi),
llamados número
pi, número e y número de
oro, respectivamente. Dos de ellos, p
y f, ya eran conocidos
por los griegos, varios siglos antes de Cristo; el número e
es ampliamente utilizado desde el siglo XVIII. |
|
- Desde antigüedades
muy remotas se sabe que en todas las circunferencias la relación
entre su longitud y su diámetro da siempre el mismo resultado;
ese resultado se ha venido designando con la letra griega p,
que es la inicial de la palabra griega periferia (periferia).
El valor de p ha sido una
preocupación constante entre los matemáticos desde
el siglo III antes de Cristo; durante muchos siglos se creyó
que p era igual a alguna fracción
de dos enteros y hubo muchos intentos por encontrarla, pero sólo
se obtuvieron aproximaciones notables, tales como
- p
= 22/7 = 3,1428... (Arquímedes, siglo III a.C.)
- p
= 377/120 = 3,14166..., (Ptolomeo, siglo II d.C.)
- p
= 355/113 = 3,141592.., (Tsu Ch'ung-Chi, siglo V, dC)
Quizá
el caso más llamativo sea el del inglés William
Shanks, que dedicó 20 años de su vida a la obtención
de cifras decimales de p.
A finales del siglo XIX, dio 707 decimales de p,
pero, en 1945, se descubrió que había cometido
un error en el decimal 528, y a partir de ahí los demás
eran incorrectos.
|
|
- En 1767 el
matemático Johann Lambert demostró que p
no podía expresarse en forma de fracción, es decir,
que p era irracional, por
lo que todos los esfuerzos se centraron ya en conseguir fórmulas
cada vez mejores para dar buenas aproximaciones de p.
De hecho algunas fórmulas ya habían sido obtenidas
antes de demostrar la irracionalidad de p,
tales como
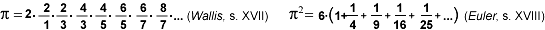
- Cualquier
número obtenido después de un número finito
de pasos a partir de enteros, usando sólo con ellos las
operaciones suma, resta, multiplicación, división
y radicación, se llama número algebraico
(Dicho de otro modo, los números algebraicos son
aquellos que son solución de alguna ecuación polinómica
de coeficientes enteros.). Euler, en el siglo XVII, llamó
trascendentes a los números que no eran algebraicos,
es decir, trascendentes porque trascienden más allá
de las operaciones habituales del álgebra. Hasta el
siglo XIX no se conoció el primer número trascendente,
y fue a finales de es mismo siglo, en 1882, cuando Lindemann demostró
que p es trascendente.
- El descubrimiento
de Lindemann permitió resolver de paso uno de los tres
problemas clásicos de la antigüedad, el de la
cuadratura del círculo; al ser p
trascendente, la cuadratura del círculo era imposible.
- p
aparece en muchas cuestiones que nada tienen que ver con circunferencias.
Por ejemplo,
- Imagina
que tomamos al azar dos números en la serie natural
(1, 2, 3, 4, ...). ¿Te imaginas cuántas posibilidades
tenemos de que los números tomados no tengan ningún
factor común? La respuesta es sorprendente (y difícil
de obtener): En el 6/p%
= 1,91% de los casos habremos cogido dos números primos
entre sí (o sea, sin ningún factor común)..
- Imagina
que tomamos al azar dos números decimales positivos
menores que 1. ¿Te imaginas cuánto vale la probabilidad
de que esos dos números junto con el número
1 puedan ser los lados de un triángulo obtusángulo?.
La respuesta vuelve a ser sorprendente: Es (p-2)/4=0'2878,
luego eso será posible en el 28'78% de los casos.
- Una anécdota
curiosa sobre el número p.
- Ocurrió
en el año 1897 en Indiana, EE.UU., y el protagonista
fue un médico llamado Goodwin, quien creyó haber
realizado un descubrimiento sobre la relación entre el
círculo y la circunferencia, lo que implicaba un impresionante
resultado acerca de p.
Llevó el caso al terreno político pidiendo a su
representante en la Asamblea General de Indiana que presentara
como proposición de Ley local el siguiente texto: "La
Asamblea General del estado de Indiana decreta que se ha descubierto
que el área del círculo es igual al cuadrado que
tiene el lado de longitud igual al cuadrante de la circunferencia".
Es inmediato deducir de ello que p=4.
La proposición se presentó y pasó la aprobación
de un primer comité, poniéndose con ello en marcha
un procedimiento para ser aprobada por el pleno del Senado,
con lo que habría adquirido el rango de ley. Afortunadamente
para "los padres de las leyes", fue retirada en el
último momento, con lo que se evitó caer en un
ridículo que habría adquirido el rango de histórico.
- Ver
más sobre el número p
|
|
El
número e, y su eterna compañera la función
logaritmo neperiano, tienen numerosas aplicaciones en todas
las ramas de la ciencia, la economía, etc. Antes de indicar
algunas de ellas, veamos 3 definiciones, diferentes pero equivalentes,
de este número (también irracional y trascendente,
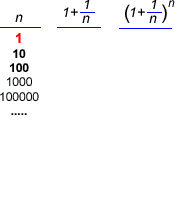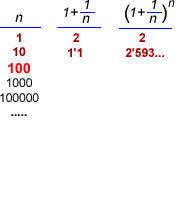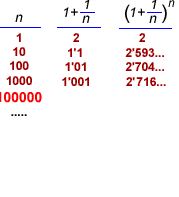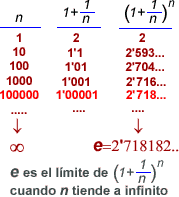
como p), cuyo valor aproximadamente
es: e = 2'718,,,
|
Definición
1
|
Definición
2
|
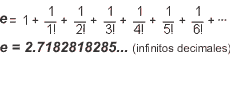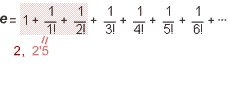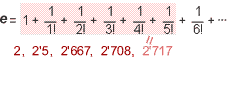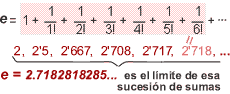
Definición
3
|
Algunos ejemplos de aplicación
- ¿Te
has preguntado alguna vez cuál es la forma más rentable
de cobrar el interés ofrecido por un Banco?
- Si invertimos
un capital a un interés compuesto anual del 10% (tema
del que todo el mundo suele saber), la fórmula que
establece lo que recogeremos al cabo de n años es
- Pero, ¿sería
preferible si nos lo pagaran cada 6 meses a razón del 5%?
¿Sería incluso mejor que nos lo pagaran cada mes
a razón del 1%? ¿Tal vez que nos lo pagaran diariamente
al 10/365% =0' 0274%? Si pensamos en lo que cogeríamos
en un solo año, poniendo 1 euro, vemos que
- Ya puestos,
¿por qué no imaginar que nos dan el interés
por horas, o por minutos, o por segundos,
o...¡de manera continua!? No sería tal vez
ésta la mejor de las formas posibles? Lo cierto es que
sí, que es la forma que nos daría el mejor rendimiento
posible para un 10% anual. Ese rendimiento, para 1 euro sería,
lógicamente, el valor límite de la expresión
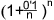cuando n tiende a infinito, el cual resulta ser  .
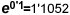- Ese crecimiento
continuo al que nos acabamos de referir no es nada extraño
en el mundo animal. Los modelos propuestos por economistas,
biólogos, etc para estudiar crecimientos de poblaciones
suelen basarse en la idea anterior, y acaban en fórmulas
que inevitablemente incluyen potencias del número e
con la variable tiempo en el exponente.
- ¿Te
has preguntado alguna vez cómo dieron los científicos
con una fórmula para averiguar la edad de un esqueleto,
un fósil, etc? ¿Sabes que también el
conocimiento del número e fue fundamental?
- A mediados
del siglo XX, el químico Libby descubrió
el carbono-14, un isótopo radiactivo del carbono
que desaparece lentamente (su
vida media es de 5568 años, es decir, una cantidad
dada de C14 tarda 5568 años en reducirse a la mitad).
El C14 reacciona con el oxígeno en las capas altas
de la atmósfera dando dióxido de carbono radiactivo,
el cual entra en la superficie de la Tierra, en la que se
desarrolla la vida. Libby decía: Como las
plantas viven del dióxido de carbono, tendrán
todas algo de radiactividad, y lo mismo ocurrirá con
los animales terrestres, ya que viven de ellas. Mientras
un ser está vivo, va reponiendo el C14 que pierde,
pero cuando ese ser muere, sólo se producirá
en él una pérdida continua y lenta de C14.
- Una vez
que los químicos consiguieron llegar a medir la cantidad
de C14 contenida en un ser no vivo, como se conocía
la velocidad de desintegración del C14, se podía
pensar en llegar a una ecuación que les diera como
solución el tiempo necesario para que en ese
ser quedara tan solo esa cantidad de C14, suponiendo razonablemente
que en los animales y plantas vivos del pasado existían
cantidades similares a las de ahora. Sólo quedaba,
pues, encontrar una fórmula que involucrara la cantidad
inicial (CI) de radiactividad, la cantidad
actual (CA) y el tiempo (t). Pues
bien, la fórmula encontrada fue
(En
la fórmula, Ln2 = 0'69315 es el número al que
hay que elevar e para obtener resultado igual a 2)
|
 |
- El número
f, llamado número de oro,
es una de las dos soluciones de la ecuación X
² = 1-X.
Concretamente,
|
|
La otra solución
es, precisamente, 1/f =
1,618...
- El número
f aparece
en campos tan variados como los reinos vegetal y animal, la poesía,
la música, la arquitectura, el arte, etc. y se designa
con la letra griega "fi" en honor de Fidias,
considerado el escultor de las obras más perfectas de la
antigua Grecia.
-
Desde
hace cinco siglos, el rectángulo considerado como "el
más bello" es aquel en el cual la relación
entre la altura y la anchura da resultado igual
a f.
-
El
rectángulo
"más bello" tiene la propiedad de que al quitarle
el cuadrado más grande posible, o sea, el de lado igual
al lado menor, resulta otro rectángulo más pequeño
que también es de "máxima belleza" (Fíjate
en la igura 2)
-
Así,
podríamos continuar el proceso de división con
este rectángulo menor e iríamos obteniendo rectángulos
cada vez más pequeños, los cuales serían
siempre de "máxima belleza". Luego, uniendo
los extremos de esos cuadrados obtendríamos la llamada
espiral áurea, presente en objetos naturales
tales como la concha del Nautilus, la distribución
de semillas del girasol, el feto humano, etc. (figura 3,
Nautilus)
- Según
las tradiciones que proponen un canon de belleza del cuerpo humano,
si tomamos 1 como medida total del cuerpo, entonces la medida
de los pies al ombligo debe ser exactamente f.
(figura 4, ideal de L. da Vinci)
- Leonardo
de Pisa, apodado Fibonacci, planteó en el siglo
XIII un problema sobre reproducción de conejos que daba
como resultado la sucesión
1, 1,
2, 3, 5, 8, 13, 21, ....,
Dicha sucesión
tiene importantes en Ciencias de la Naturaleza y cada término
de ella se obtiene sumando los dos anteriores a él. Curiosamente,
si vas dividiendo cada término por su siguiente en la
sucesión, verás que salen aproximaciones cada
vez mejores del número de oro. Eso no es extraño,
ya que en realidad el límite de tales divisiones es el
número de oro.
Ver
más sobre el número de oro
|
|
|
|
|
El hombre de Vitubrio
Para
Leonardo da Vinci, las dimensiones a y b en
el cuerpo perfecto deben dar un cociente igual a 0'618....
|
|
|
|
No hay comentarios:
Publicar un comentario